
|
|
Операции над высказываниями.Лекция №4 Математические предложения Высказывания и их логическое значение. Что такое алгебра логики? Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. Опр. Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, "6 – четное число" – высказывание, т.к. оно истинное. "Рим – столица Франции" тоже высказывание, так как оно ложное. Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения "ученик десятого класса" и "информатика – интересный предмет". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие "интересный предмет". Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла. Предложения типа "в городе А более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами. Опр. Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Введем обозначения: истина – 1 (и); ложь – 0 (л) Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если..., то", "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. Опр. Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Опр. Высказывания, не являющиеся составными, называются элементарными. Например, из элементарных высказываний "Петров – врач", "Петров – шахматист" при помощи связки "и" можно получить составное высказывание "Петров – врач и шахматист", понимаемое как "Петров – врач, хорошо играющий в шахматы". При помощи связки "или" из этих же высказываний можно получить составное высказывание "Петров – врач или шахматист", понимаемое в алгебре логики как "Петров или врач, или шахматист, или и врач и шахматист одновременно". Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний. Чтобы обращаться к логическим высказываниям, им назначают имена. Высказывания обозначаются заглавными буквами латинского алфавита. Пусть А – высказывание "Тимур поедет летом на море", а В – высказывание "Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом побывает и на море, и в горах" можно кратко записать какА и В. Здесь "и" – логическая связка, А, В – логические переменные, которые могут принимать только два значения – "истина" или "ложь", обозначаемые, соответственно, "1" и "0". Операции над высказываниями. Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение: 1.Отрицание– выражается словом "не", обозначается чертой над высказыванием Опр. Отрицанием высказывания Пример. "Луна – спутник Земли" (А); "Луна – не спутник Земли" ( Таблица истинности:
2.Дизъюнкция – выражается связкой "или", обозначается символом « Опр. Дизъюнкцией двух высказываний Таблица истинности:
Например, высказывание "10 не делится на 2 или 5 не больше 3" – ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3"— истинны. 3.Конъюнкция – выражается связкой "и", обозначается символом « Опр. Конъюнкцией двух высказываний Таблица истинности:
Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3"— ложны. 4.Импликация – выражается связками «если ..., то», «из ... следует…», «... влечет ...», обозначается символом « Опр. Импликацией двух высказываний Таблица истинности:
Например, высказывания: «данный четырёхугольник – квадрат» (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание Ложен только один вариант, когда А истинно, а В ложно, т.е. «данный четырёхугольник является квадратом, но около него нельзя описать окружность». В обычной речи связка "если ..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США – демократ, то в Африке водятся жирафы", "если арбуз – ягода, то в бензоколонке есть бензин". 5.Эквиваленция – выражается связкой слов «…тогда и только тогда, когда …». Обозначается символом « Опр. Эквиваленцией двух высказываний Таблица истинности:
Например, высказывания: «24 делится на 6 тогда и только тогда, когда 24 делится на 3», «23 делится на 6 тогда и только тогда, когда 23 делится на 3» – истинны, а высказывания: «24 делится на 6 тогда и только тогда, когда 24 делится на 5», «21 делится на 6 тогда и только тогда, когда 21 делится на 3» – ложны. Высказывания Например: «3 больше 2» – (А), «пингвины живут в Антарктиде» – (В). Образованное из высказываний А и В составное высказывания 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 или
или 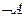
 называется высказывание
называется высказывание  , которое истинно когда
, которое истинно когда 

 », т.е.
», т.е.  –
–  или
или  .
. », т.е.
», т.е.  –
–  », т.е.
», т.е.  , и читается «если
, и читается «если  », т.е.
», т.е.  , и читается «
, и читается «