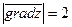|
|
Дифференциалы высших порядковДана функция z=f(x,y), дифференцируемая в точке х. Было ранее установлено, что dz=fx’(x,y)dx+fy’(x,y)dy ,где х и у независимые переменные. Зафиксируем dx и dy. Опр. Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка и обозначается: d2 z=d(dz)=d(fx(x,y)dx+fy(x,y)dy)=d(fx’(x,y)dx)+d(fy’(x,y)dy)= =d(fx’(x,y))dx+d(fy’(x,y))dy=((fxx’’(x,y))dx+(fxy’’(x,y))dy)dx+(f(yx’’(x,y)dx+fyy’’(x,y)dy)dy=fxx’’(x,y)dx2+2fxy’’(x,y)dxdy+fyy’’(x,y)dy2 d2z=fxx’’(x,y)dx2+2fxy’’(x,y)dxdy+fyy’’(x,y)dy2
Дифференциал третьего порядка
Символически дифференциалы различных порядков можно записать следующим образом:
Замечание Дифференциалы высших порядков свойством инвариантности не обладают. Рассмотрим dz=fx’(x,y)dx+fy’ (x,y)dy ,где х и у являются некоторыми функциями от других переменных. В этом случае dx и dy фиксировать нельзя. Тогда d2z= d(dz)=d(fx’(x,y)dx + fy’(x,y)dy)= = d(fx’(x,y)dx )+ d(fy’(x,y)dy)={по свойству дифференциалов, что d(u.v)=v.du+u.dv}= d(fx’(x,y))dx+ fx’(x,y)d(dx)+d(fy’(x,y))dy+fy’(x,y)d(dy) = (fxx’’(x,y)dx+fxy’’(x,y)dy)dx+fx’(x,y)d2x+(fyx’’(x,y)+fyy’’(x,y)dy)dy+fy’(x,y)d2y= =fxx’’(x,y)dx2+2fxy’’(x,y)dxdy+fyy’’(x,y)dy2+fx’(x,y)d2x+fy’(x,y)d2y Форма дифференциалов изменилась. Пример. Найти дифференциал второго порядка z=ln(x3+y2)
Касательная плоскость и нормаль поверхности
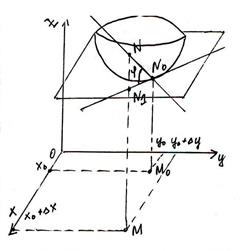
Опр.Касательной плоскостью поверхности z=f(x,y) d в точке No, называется плоскость, для которой угол между этой плоскостью и секущей NoN стремится к нулю при стремлении точки N к No по поверхности.
Касательная плоскость либо существует в точке, либо не существует.
Например, возьмём поверхность:
Частные производные в точке (0,0,0,) не существуют, значит функция не дифференцируема в этой точке.
Пусть функция дифференцируема в точке (x0,y0). Покажем, что плоскость, заданная уравнением z-z0=fx’(x0,y0)(x-x0)+fy’(x0,y0)(y-y0) является касательной поверхностью.
Дадим
=
Известно, что т.к. функция дифференцируема, то ее точное приращение представимо в виде:
z-z0 где
Опр.Прямая, проходящая через точку касания перпендикулярно касательной плоскости, называется нормалью поверхности в данной точке.
Уравнение нормали
Тогда уравнение нормали запишется:
Пример. Написать уравнение касательной плоскости и нормали с кооординатами
Уравнение касательной плоскости:
Уравнение нормали:
Уравнение касательной плоскости поверхности, заданной неявно
Поверхность задана неявно уравнением: F(x,y,z)=0. По правилу дифференцирования неявных функций известно, что:
Тогда Подставим в уравнение:
Уравнение нормали
Пример. Написать уравнение касательной плоскости и норали к поверхности F(x,y,z) , заданной неявно x(y+z)(xy-z)+8=0 в точке (2;1;3), которая лежит на поверхности.
Уравнение плоскости: 4(x-2)+14(y-1)-10(z-3)=0; 2x+7y-5z+4=0
Уравнение нормали:
Производная по направлению Дана функция U=f(x,y,z), дифференцируемая в точке M(x,y,z). Дадим x,y,z приращение
Т.к. функция u=f(x,y,z) дифференцируема в точке M(x,y,z), то её полное приращение представимо в виде:
где Разделим обе части равенства на
Но:
Тогда: Перейдём к пределу при
Опр. Если существует предел функции u=f(x,y,z) по направлению S и обозначается:
Пример. Найти производную функции u=xy2+z3-xyz в точке М(1;1;2) в направлении, образующимся осями координат (углы:60°,45°,30°).
Градиент функции Дана функция u=f(x,y,z) Опр.Вектор, координатами которого являются частные производные от функции u=f(x,y,z), называется градиентом функции и обозначается:
Пример. Найти точки, в которых модуль градиента функции
Во всех точках окружности с радиусом 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


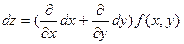
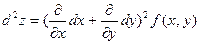
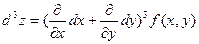



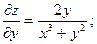
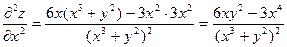

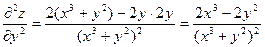
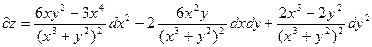
 Дана функция z=f(x,y), дифференцируемая в точке N0(x0,,y0,,z0). Графиком её является некоторая поверхность.
Дана функция z=f(x,y), дифференцируемая в точке N0(x0,,y0,,z0). Графиком её является некоторая поверхность. при
при 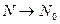 ;
;
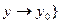
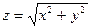
 ;
;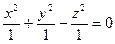
 в точке (0,0,0) касательная к плоскости не существует, т.к.:
в точке (0,0,0) касательная к плоскости не существует, т.к.: 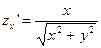 ;
;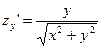
 и
и  приращения
приращения 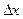 и
и 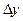 .
.
 =
=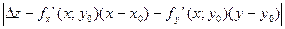
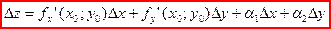 ,
, - бесконечно малые при
- бесконечно малые при  т.е. мы имеем, что:
т.е. мы имеем, что:  при
при  , при этом
, при этом 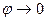 . Значит, рассматриваемая плоскость является касательной.
. Значит, рассматриваемая плоскость является касательной. Уравнение касательной перепишем в виде:
Уравнение касательной перепишем в виде: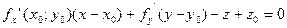

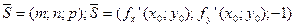
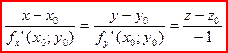
 в точке
в точке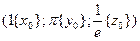
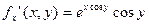

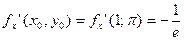


 ,
,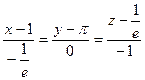
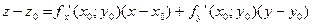
 и
и 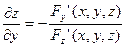
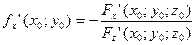
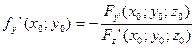
 {умножим на произведение и перенесем влево}
{умножим на произведение и перенесем влево}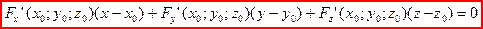
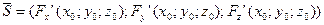

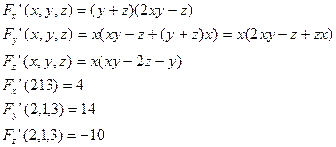
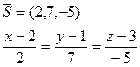
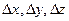 .
. Соединим M и N. Проведем диагональ и обозначим вектор
Соединим M и N. Проведем диагональ и обозначим вектор  Известны направляющие косинусы
Известны направляющие косинусы 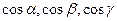
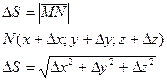
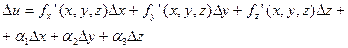
 бесконечно малые при
бесконечно малые при  т.е.
т.е. 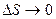
 :
: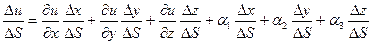
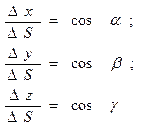
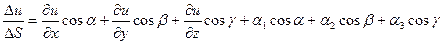
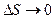 :
: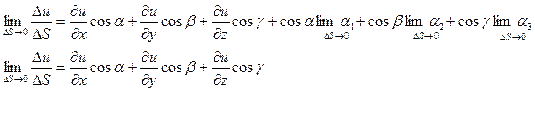
 , то он называется производной от
, то он называется производной от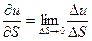
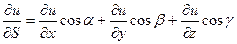
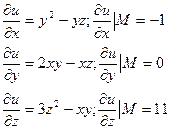

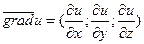
 равен 2.
равен 2. {по условию}
{по условию}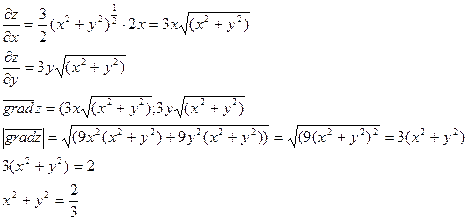
 и с центром в начале координат
и с центром в начале координат