
|
|
Примеры отношений эквивалентностиФункции и отношения
1. Декартово (прямое) произведение множеств. Определение. Примеры.
Определение: Декартово произведениемножеств А и В, обозначаемое АхВ, есть множество {(a,b) : aEA и bEB}. Объект (a,b) называется упорядоченной паройс первой компонентой a и второй компонентой b.
Множество АхВ состоит из всех упорядоченных пар, имеющих в качестве первой компоненты элемент из a, а второй из В. По существу, это та же упорядоченная пара, которую мы обычно используем в алгебре. Порядок компонент в паре существенен! Например, рисуя график функции, мы знаем, что точка (1,2) не совпадает с точкой (2,1).
Пример 1 Пусть А={1,2,3}, а В={x,y}, тогда АхВ={(1,x), (1,y), (2,x, (2,y), (3,x), (3,y)}.
Если каждое множество из А и В представляет собой множество действительных чисел, то АхВ представляет собой декартову плоскость, на которой упорядоченные пары чисел используются для графического изображения функций. Если А содержит n элементов, а В содержит m элементов, тогда АхВ содержит n∙m элементов. В частности, если А пусто или В пусто, то, по определению, АхВ пусто. Также декартово произведение называют прямым произведением множеств.
Декартовым произведением произвольного числа множеств А1, А2, …, Аn называется множество
Элементы этого множества — просто конечные упорядоченные наборы, объекты, с которыми работают все языки программирования. Подмножества прямых произведений также представляют собой объект обработки в базах данных.
Характеристические вектора (о них было в лекциях, хотя это булева алгебра уже)
U = {1 2 3 4 5 6 7 8 9} A = {2 4 6 8}
2. Определение отношения. Примеры. Композиция отношений. Примеры.
Определение: Отношением R множеств А и В называется произвольное множество АхВ. Если (a,b) E R, это записывают как аRb, при этом говорят, что а и b находятся в отношении R, или просто, что а относится к b. Если А=В, то отношение есть подмножество АхА; такое отношение называют бинарным отношением.
В том случае, когда А равно В, мы просто говорим об отношении R на А.
Там их еще много можно придумать))
Композиция отношений
Пример 1
а вообще я лучше ссылку вставлю http://www.diary.ru/~eek/p58898977.htm?oam#more1
Композиции с ориентированными графами посмотрите в Хагарти, стр. 94
3. Бинарные отношения. Рефлексивность. Примеры. 4. Бинарные отношения. Симметричность. Примеры. 5. Бинарные отношения. Антисимметричность. Примеры. 6. Бинарные отношения. Транзитивность. Примеры.
Свойства отношений:
1. Рефлесивность. 2. Симметричность. 3. Антисимметричный. 4. Транзитивность.
Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения. Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др. Существуют отношения, не обладающие свойством рефлексивности, например, отношение перпендикулярности отрезков: a Не обладает свойством рефлексивности и отношение «длиннее» для отрезков, «больше на 2» для натуральных чисел и др. Отношение R на множестве Х называется антирефлексивным, если для любого элемента из множества Х всегда ложно хRх: Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны сами себе, а точки, не лежащие на прямой l, себе не симметричны. Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении с элементом y, следует, что и элемент y находится в отношении R с элементом х: xRy Граф симметричного отношения обладает следующей особенностью: вместе с каждой стрелкой, идущей от х к y, граф содержит стрелку, идущую от y к х. Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др. Существуют отношения, которые не обладают свойством симметричности. Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Граф этого отношения обладает особенностью: стрелка, соединяющая вершины, направлена только в одну сторону. Отношение R называют антисимметричным, если для любых элементов х и y из истинности xRy следует ложность yRx: : xRy Кроме отношения «длиннее» на множестве отрезков существуют и другие антисимметричные отношения. Например, отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др. Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности. Отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRz Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z. Свойством транзитивности обладает и отношение «длиннее» на множестве отрезков: если отрезок а длиннее отрезка b, отрезок b длиннее отрезка с, то отрезок а длиннее отрезка с. Отношение «равенства» на множестве отрезков также обладает свойством транзитивности: (а=b, b=с) Существуют отношения, которые не обладают свойством транзитивности. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку b, а отрезок b перпендикулярен отрезку с, то отрезки а и с не перпендикулярны!
7. Доказательство теоремы о разбиении множества на классы эквивалентности. 8. Отношения эквивалентности. Классы эквивалентности. Определения. Примеры.
Отношением эквивалентности называется рефлексивное, симметричное и транзитивное бинарное отношение на множестве А.
Отношение эквивалентности в некотором смысле обобщает понятие равенства.
Эквивалентные элементы (т. е. находящиеся в отношении эквивалентности), как правило, обладают какими-то общими признаками.
Примеры наводят на мысль, что если на множестве задано отношение эквивалентности, то все его элементы можно естественным способом разбить на непересекающиеся подмножества. Все элементы в любом из таких подмножеств эквивалентны друг другу с самом прямом смысле. Наличие такого разбиения — движущая сила любой классификационной системы.
Разбиением множества А называется совокупность не пустых подмножеств А1, А2, …, Аn множества А, удовлетворяющих следующим требованиям:
Подмножества Аi называются блоками разбиения. Диаграмма Венна разбиения множества А изображена на рисунке
Блоки разбиения не могут иметь общих элементов.
Примеры отношений эквивалентности · Отношение равенства(=) является тривиальным примером отношения эквивалентности на любом множестве. · Отношение равенства по модулю · Отношение параллельности прямых на плоскости. · Отношение подобия фигур на плоскости. · Отношение равносильности на множестве уравнений. · Отношение связности вершин в графе. · Отношение быть одного роста на множестве людей.
12. Отношения частичного порядка. Примеры.
Частичным порядком называется рефлексивное, транзитивное, но кососимметрическое отношение R на множестве А. Частичный порядок важен, когда мы хотим охарактеризовать старшинство (решить, при каких условиях один элемент превосходит другой).
Примеры частичных порядков: · «≥» на множестве вещественных чисел
Множества с частичным порядком называют частично упорядоченными множествами.
Если R — отношение частичного порядка на множестве А, то при х≠у и хRy мы называем х предшествующим элементом или предшественником, а у — последующим. У произвольно взятого элемента у может быть много предшествующих элементов. Однако если х предшествует у, и не существует таких элементов z, для которых хRz и zRy, мы назовем х непосредственным предшественником у и пишем
11. Отношение линейного порядка. Примеры.
Линейным порядком на множестве А называется отношение частичного порядка, при котором из любой пары элементов можно выделить предшествующий и последующий.
Примеры линейного порядка: · «≥» на множестве вещественных чисел; · лексикографическое упорядочение слов в словаре.
9. Отношения строгого порядка. Примеры.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|













 b, b
b, b 
 .
.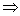 yRx .
yRx .
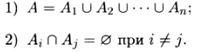



 :
:  на множестве целых чисел.
на множестве целых чисел.


