
|
|
Соединения с повторениямиЭлементы комбинаторики. Комбинаторные методы обработки информации. Комбинаторика является разделом дискретной математики, изучающим некоторые операции над конечными множествами, такие как упорядочение множества и разбиение множества, интересуется расположением элементов в множестве, выясняет, сколькими способами можно расположить элементы множества в том или ином порядке. Это приводит к понятиям перестановок, размещений и сочетаний. Основными задачами комбинаторики являются: 1) определение вида соединения; 2) подсчет числа соединений. Правила суммы и произведения При определении вида соединения удобно пользоваться следующей схемой:
Все расчетные формулы комбинаторики базируются на двух основных правилах: 1.Правило суммы:если объект А может быть выбран nспособами, а объект В – mспособами, то выбор «А или В» может быть осуществленn+mспособами. 2.Правило произведения:если объект А может быть выбран nспособами и после каждого из таких выборов объект В – mспособами, то выбор «А и В» в указанном порядке может быть осуществлен n⋅mспособами.
Соединения без повторений Пусть дано множество М, состоящее из n элементов. Опр. 1 Перестановки – всевозможные упорядоченные множества, составленные из всех элементов данного множества. Число всевозможных перестановок из n элементов обозначают Рn и находят по формуле Рn= n! (1), где n!= 1⋅2⋅3⋅ … ⋅n, 0!=1 по определению. Пример 1.Сколько перестановок можно составить из трех букв а, в, с? Решение: Р3=1⋅2⋅3=6. Действительно: авс, вас, асв, сав, вса, сва.♦ Пример 2.Сколькими способами можно переставить буквы в слове «треугольник»? Решение: Т.к. все буквы в данном слове разные, т.е. нет повторений, то можно воспользоваться формулой (1): Р11=11!=39916800.♦ Опр. 2 Размещениями из nпо mназываются всевозможные упорядоченные подмножества, содержащие m элементов из данных n. Обозначаются и вычисляются по формуле:
Пример 3.Сколько можно составить четырехзначных чисел, содержащих различные цифры из 5 цифр. Решение: Четырехзначное число – это упорядоченная последовательность цифр, т.е. имеем дело с размещениями без повторений:
Пример 4.В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день? Решение: Опр. 3 Сочетаниями из nпо mназываются всевозможные подмножества данных n элементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:
Пример 5.Сколькими способами можно из 7 различных открыток выбрать три? Решение: Совокупность трех открыток является неупорядоченным подмножеством семи открыток, поэтому имеем дело с сочетаниями:
Пример 6.Из группы в 25 человек нужно выбрать троих для работы на субботнике. Решение. Если выбирать их последовательно, сначала первого, потом второго, потом третьего, то получим 25* 24* 23 Но так как нас не интересует порядок выбора, а только количество выбранных человек: 25!/(3!*22!) Соединения с повторениями Опр: 4 Перестановками с повторениями называются перестановки из n элементов, в каждую из которых входит n1 элементов а, n2 элементов b, …, nk элементов l, где n=n1+n2+…+nk. Число перестановок с повторениями вычисляется по формуле:
Пример 7.Сколькими способами можно переставить буквы в слове “математика”. Решение: В слове “математика” есть повторяющиеся буквы: “м” – 2 раза, “а” – 3 раза, “т” – 2 раза, “е” – 1 раз, “и” – 1 раз, “к” – 1 раз. Порядок расположения элементов имеет значение (это очевидно, так как если переставить местами 2 буквы, то получатся разные слова) и все элементы используются, следовательно, это перестановка с повторениями.
Таким образом, в слове “математика” можно переставить буквы 151200 способами. Опр 5 Сочетания из n элементов, в каждое из которых входит m элементов, причем один и тот же элемент может повторяться в каждом сочетании любое число раз, но не более m, называются сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле:
Пример 8.На почте продаются открытки 10 сортов. Сколько вариантов существует для покупки 12 открыток. Решение: Порядок расположения элементов не имеет значения, следовательно, это сочетание. А так как открытки в наборе могут повторяться, то это сочетание с повторениями.
Таким образом, из 10 открыток можно выбрать набор из 12 штук 293930 способами. Опр. 6 Размещениями с повторениями из n элементов по k элементов называются упорядоченные множества, каждое из которых содержит k необязательно различных элементов из данного множества n элементов. Число размещений с повторениями вычисляется по формуле:
Пример 9.В стену здания вмонтированы 8 гнезд для флажков. В каждое гнездо вставляется либо голубой, либо красный флажок. Сколько различных случаев распределения флажков на здание. Решение: Так как порядок расположения элементов важен и не все элементы используются в данном соединении, то это размещение. А так как всего 8 гнезд, а флажков 2 вида (голубой и красный), то они будут повторяться, т.е. это размещение с повторением.
Таким образом, существует 256 способов украсить здание с 8 гнездами флажками двух цветов. Если имеются ограничения на количество разных предметов, которые можно помещать на позиции. В этом случае число перемещений рассчитываться по формуле: A = k1* k2*k3 *...*kn (2) Пример 10.В эстафете 100, 200, 400, 800 метров на первую позицию тренер может выставить одного из 3 бегунов, на вторую - одного из 5, на третью - одного из 6, на четвертую - единственного бегуна (на каждую позицию выставляются разные бегуны). Сколько вариантов расстановки участников эстафетного забега может составить тренер? Решение:В соответствии с формулой получаем, что число вариантов равно: 3 * 5 * 6 * 1 = 90. Пример 11.Сколько различных трехзначных чисел можно составить из цифр 0, 1, 2, 3? Решение: На первое место в трехзначном числе можно выбрать любую цифру их трех (кроме нуля), после каждого такого выбора на второе место можно поставить любую цифру из оставшихся трех, на третье – из оставшихся двух. По правилу 2 получим: 3⋅3⋅2=18 чисел.♦ Примеры решения задач Пример 1. Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет. Решение: Порядок расположения элементов имеет значение и в диаграмме 4 столбца, а ручка тоже четырехцветная, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска столбцов не повторяется (в условии сказано, что столбцы имеют разные цвета), то это перестановка без повторения. Итак, Pn = n! = 4! = 1⋅2⋅3⋅4 = 24 Ответ: столбцы можно закрасить 24 способами. Пример 2. Имеется 5 кружков: 3 белых и 2 черных. Сколько различных узоров можно получить, располагая кружки в ряд. Решение: Порядок расположения элементов имеет значение и в узоре 5 кружков, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска кружков повторяется (в условии сказано, что 3 белых и 2 черных), то это перестановка с повторением. Итак, Ответ: узор можно составить 10 способами. Пример 3. Сколько словарей надо издать, чтобы можно было непосредственно выполнить перевод с любого из 5 языков на любой из 5 языков. Решение: Порядок имеет значение (так как русско-английский и англо-русский словари различны) и не все элементы присутствуют в соединении (а только 2 из 5), значит, это размещение. Так как языки различны, то это размещение без повторения. Итак, Ответ: надо составить 20 словарей. Пример 4. На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных комбинаций их сигналов, если каждый светофор имеет 3 состояния. Решение: Порядок имеет значение и не все элементы присутствуют в соединении, значит, это размещение. Так как цвета повторяются, то это размещение с повторением. Итак, Ответ: может быть дано 243 различных комбинаций цветов. Пример 5. 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой. Решение: Порядок расположения игроков в команде не имеет значения, следовательно, это сочетание. А так как игроки не повторяются (все члены команды различные люди), то это сочетание без повторения. Итак,
Ответ: игроки могут разбиться на команды по 4 человека в каждой 495 способами. Пример 6. В цветочном магазине продаются цветы 6 видов. Сколько можно составить букетов из 10 цветов в каждом (букеты отличающиеся лишь расположением цветов считать одинаковыми). Решение: Порядок расположения цветов в букете не имеет значения, следовательно, это сочетание. А так как цветы повторяются, то это сочетание с повторением. Итак, Ответ: букеты можно составить 3003 способами. Пример 7. В группе 25 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника. Решение: Сначала узнаем сколькими способами можно выбрать 3 хорошистов из 11 человек. Порядок расположения студентов не важен, значит, это сочетание. А так как люди в группе не повторяются, то это соединение – сочетание без повторения. Итак, одного хорошиста можно выбрать Ответ: группу для выполнения лабораторной работы можно составить 3300 способами. Пример 8:Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку. Решение: Выберем для 3 человек чашки из 4 имеющихся. Порядок расположения элементов имеет значение, и не все элементы входят в соединение, значит, это размещение. Но так чашки не повторяются, то это размещение без повторения. Итак, из 4 чашек 3 можно выбрать Ответ: стол можно накрыть 172800 способами. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 (2)
(2) =5⋅4⋅3⋅2=120. ♦
=5⋅4⋅3⋅2=120. ♦ ♦
♦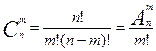 (3).
(3). ♦
♦
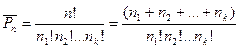
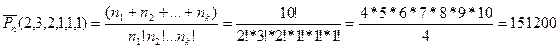
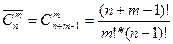
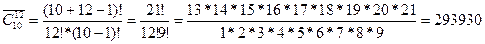

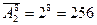
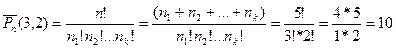

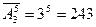
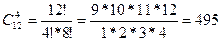
 =3003
=3003 способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать
способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать 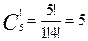 способами и одного троечника можно выбрать
способами и одного троечника можно выбрать  способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим:
способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим:  способами.
способами. способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать
способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать  способами, а из 6 ложек 3 можно выбрать
способами, а из 6 ложек 3 можно выбрать  способами. Так как блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть
способами. Так как блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть  *
* 
 =24*60*120=172800 способами.
=24*60*120=172800 способами.