Это неоклассическая функция.
Пример:  , где a > 0, b < 1 , где a > 0, b < 1
| | | |  |
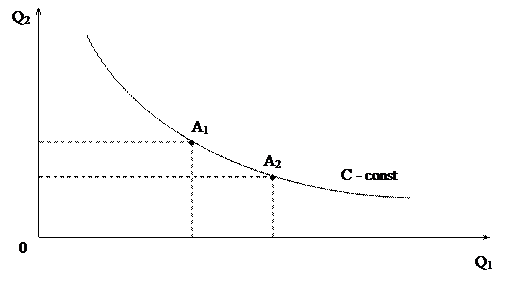 Общее положение: для описания поведения потребителя можно использовать особую функцию с перечисленными свойствами (неоклассическая функция потребления).Экономический смысл: мы рассматриваем пространство товаров, в котором мы можем рассмотреть различные уровни полезности (C – значение полезности). qi > 0 означает, что все товары необходимы. Свойство 2a показывает, как изменится полезность набора, если увеличить на единицу количество одного из благ – предельная полезность (Uj). В свойство 2b показывает: если в одном наборе мы последовательно наращиваем количество одного из благ, то предельная полезность уменьшается – закон Госсена.Отныне мы можем считать, что каждый потребитель имеет собственную функцию полезности. С помощью этой функции он может определить полезность любого уровня благ. Если C – число, то возвращаемся к количественному подходу. Если C нельзя определить до числа, то остаемся в рамках порядкового подхода. Количественный и порядковый подход не противоречивы.АНАЛИЗ КРИВЫХ БЕЗРАЗЛИЧИЯ:Требуется определить, как происходит эквивалентное замещение одного блага другим? Условие задачи:Пусть изменяется количество блага q1. Необходимо определить, насколько должно измениться количество q2, чтобы общая полезность набора не уменьшилась (q2 – ?). Общее положение: для описания поведения потребителя можно использовать особую функцию с перечисленными свойствами (неоклассическая функция потребления).Экономический смысл: мы рассматриваем пространство товаров, в котором мы можем рассмотреть различные уровни полезности (C – значение полезности). qi > 0 означает, что все товары необходимы. Свойство 2a показывает, как изменится полезность набора, если увеличить на единицу количество одного из благ – предельная полезность (Uj). В свойство 2b показывает: если в одном наборе мы последовательно наращиваем количество одного из благ, то предельная полезность уменьшается – закон Госсена.Отныне мы можем считать, что каждый потребитель имеет собственную функцию полезности. С помощью этой функции он может определить полезность любого уровня благ. Если C – число, то возвращаемся к количественному подходу. Если C нельзя определить до числа, то остаемся в рамках порядкового подхода. Количественный и порядковый подход не противоречивы.АНАЛИЗ КРИВЫХ БЕЗРАЗЛИЧИЯ:Требуется определить, как происходит эквивалентное замещение одного блага другим? Условие задачи:Пусть изменяется количество блага q1. Необходимо определить, насколько должно измениться количество q2, чтобы общая полезность набора не уменьшилась (q2 – ?).
Решение задачи:
Мерой эквивалентной замены 2-х благ в потреблении является специальный показатель:  – интервальная норма взаимной замены. Интервальная норма взаимной замены показывает, на сколько единиц нужно уменьшить потребление второго товара при увеличении первого товара на единицу при условии, что общая полезность неизменна. При последовательном увеличении количества одного и того же товара в наборе нам будет требоваться все меньшее количество второго товара для поддержания уровня полезности. Из этого следует два вывода:1)Ценность каждой единицы блага зависит от количества данного блага и от количества других благ, причем, чем больше данного блага в наборе, тем меньше ценность каждой последующей единицы и наоборот.2)Так как ценность благ существенно зависит от их количества, показатель интервальной нормы эквивалентной замены является очень грубым измерителем. Правильнее было бы измерять возможности эквивалентной замены благ в каждой точке кривой безразличия. – интервальная норма взаимной замены. Интервальная норма взаимной замены показывает, на сколько единиц нужно уменьшить потребление второго товара при увеличении первого товара на единицу при условии, что общая полезность неизменна. При последовательном увеличении количества одного и того же товара в наборе нам будет требоваться все меньшее количество второго товара для поддержания уровня полезности. Из этого следует два вывода:1)Ценность каждой единицы блага зависит от количества данного блага и от количества других благ, причем, чем больше данного блага в наборе, тем меньше ценность каждой последующей единицы и наоборот.2)Так как ценность благ существенно зависит от их количества, показатель интервальной нормы эквивалентной замены является очень грубым измерителем. Правильнее было бы измерять возможности эквивалентной замены благ в каждой точке кривой безразличия.
– предельная норма замещения.
MRS показывает, как изменится потребление 2-ого товара при небольшом изменение 2-ого товара при неизменном уровне полезности – та же интервальная норма, но только в точке.
О возможностях эквивалентной замены благ можно судить по показателю предельной нормы замещения. Видно, что MRS двух благ должна быть каким–то образом связана с величиной предельной полезности. Рассмотрим некоторую неоклассическую функцию U(q1, q2). Известна формула Эйлера:
Экономический смысл: если q1 растёт, то MRS падает, а U1 стремится к 0 и U2 стремится к бесконечности Þ U1/U2 ® 0. Общая тенденция: q1 растет ÞU1 падает Þ MRS быстро падает.БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ.Условие задачи:R – бюджет потребителя – количество денег, которым он обладает. Пусть известны цены товаров  . Запишем условие полного расходования бюджета потребителя. Пусть потребитель приобрел набор q1 и q2. . Запишем условие полного расходования бюджета потребителя. Пусть потребитель приобрел набор q1 и q2. 
Требуется найти все комбинации товаров, которые потребитель может приобрести при данном бюджете и данных ценах.
Решение задачи:

Экономический смысл: рассмотрим различные наборы товаров, которые потребитель желает приобрести: набор А – может пробрести; набор D – может; B – нет. Бюджетное ограничение делит все пространство на 3 части.
Свойства:
1. Наклон бюджетной линии определяется соотношением цен. 
2. Если изменится бюджетная линия, например первый товар подешевеет при ceteris paribus, при этом же бюджете потребитель сможет купить больше Þ tg увеличится.
3.  Если цены на товары неизменны, а R увеличится, бюджетная линия изменится, так что произойдет параллельный сдвиг прямой, угол останется тот же.СРАВНИТЕЛЬНАЯ СТАТИКА ПОТРЕБЛЕНИЯ.Существуют 2 модели:1)Статическая модель – исследуют по методу при прочих равных условиях. Такой метод называется сравнительная статика.2)Динамическая модель – при этом применяется несколько управляющих элементов. Исследование динамики – очень сложный вопрос.Условие задачи:Дана неоклассическая задача потребления, т.е. известны потребительские предпочтения, заданы потребительский бюджет и система цен. Определить оптимальный план закупок для данного потребителя Если цены на товары неизменны, а R увеличится, бюджетная линия изменится, так что произойдет параллельный сдвиг прямой, угол останется тот же.СРАВНИТЕЛЬНАЯ СТАТИКА ПОТРЕБЛЕНИЯ.Существуют 2 модели:1)Статическая модель – исследуют по методу при прочих равных условиях. Такой метод называется сравнительная статика.2)Динамическая модель – при этом применяется несколько управляющих элементов. Исследование динамики – очень сложный вопрос.Условие задачи:Дана неоклассическая задача потребления, т.е. известны потребительские предпочтения, заданы потребительский бюджет и система цен. Определить оптимальный план закупок для данного потребителя
Решение:Решив соответствующую задачу получим график:
Что влияет на объем закупок отдельного товара qj? Предпочтения не меняются. Тогда, в общем виде:  – функция от (N+1) переменных.Спрос на отдельно взятый товар – функция от цен и дохода – это функция покупательского спроса.Метод сравнения статики заключается в следующем: берем один из аргументов, остальные считаем заданными: – функция от (N+1) переменных.Спрос на отдельно взятый товар – функция от цен и дохода – это функция покупательского спроса.Метод сравнения статики заключается в следующем: берем один из аргументов, остальные считаем заданными:  .Рассмотрим влияние изменения дохода на покупательский спрос .Рассмотрим влияние изменения дохода на покупательский спрос  . .
Давайте рассматривать непрерывное изменение дохода. Тогда мы много раз решаем неоклассическую задачу и находим точки равновесия.
Эта линия содержит точки равновесия, она называется «доход–потребление». Это ГМТ равновесия, полученных при решении задач  при различных уровнях дохода. Каждая точка этой линии дает оптимальный покупательский набор для заданного значения дохода. Она также называется «кривая Энгеля».Что можно сказать про соотношение q1 и q2?При R1 закупки примерно в одинаковой пропорции. До R2 – некоторое предпочтение q1. Начиная с R2 потребитель практически перестает потреблять q2, т.е. происходит насыщение товаром q2.Если доход увеличивается на единицу и при этом стали потреблять q1 больше, чем q2, то q1 ценнее. Ценность товара имеет относительное значение и в существенной мере определяется уже достигнутым уровнем потребления. при различных уровнях дохода. Каждая точка этой линии дает оптимальный покупательский набор для заданного значения дохода. Она также называется «кривая Энгеля».Что можно сказать про соотношение q1 и q2?При R1 закупки примерно в одинаковой пропорции. До R2 – некоторое предпочтение q1. Начиная с R2 потребитель практически перестает потреблять q2, т.е. происходит насыщение товаром q2.Если доход увеличивается на единицу и при этом стали потреблять q1 больше, чем q2, то q1 ценнее. Ценность товара имеет относительное значение и в существенной мере определяется уже достигнутым уровнем потребления.
Можно построить другой график:
Задача Энгеля в интерпретации Торнквиста: необходимо рассмотреть всевозможные зависимости вида  и определить характерный вид кривых Энгеля по группам товаров.Торнквист вывел, что все товары можно грубо разделить на 3 группы:1)nовары первой необходимости;2)в точке А – переключение спроса, т.е., начиная с уровня RA, товары первой необходимости перестают доминировать в его потребительской корзине (этот порог часто отождествил с уровнем бедности);3)предметы роскоши. Их потребление начинается на достаточно высоком уровне R и уже неограниченно. В точке B предмет роскоши начинает превалировать над (2). и определить характерный вид кривых Энгеля по группам товаров.Торнквист вывел, что все товары можно грубо разделить на 3 группы:1)nовары первой необходимости;2)в точке А – переключение спроса, т.е., начиная с уровня RA, товары первой необходимости перестают доминировать в его потребительской корзине (этот порог часто отождествил с уровнем бедности);3)предметы роскоши. Их потребление начинается на достаточно высоком уровне R и уже неограниченно. В точке B предмет роскоши начинает превалировать над (2).
Вопрос№50 ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ.Пожалуй, самой простой формой представления производства является модель «чёрного ящика».
 ; ;
F – это земля, капитал, труд, предпринимательская способность. Но иногда удобнее рассматривать только один фактор, т.е. остальные не имеют значения. Функция может быть:1)однофакторная и однопродуктовая;2)однопродуктовая и многофакторная;3)многопродуктовая и многофакторная;Производственная функция, если задана, описывает некоторую технологию. Если задана технология, значит, есть производственная функция. Если технология задана и если мы знаем затраты F, мы можем легко вычислить выпуск Q.Конечно, существуют различные технологии, однако далее мы рассматриваем только эффективные технологии. Эффективная технология – наиболее производительная из существующих. Заданный объем выпуска – меньше ресурсов; задан объем ресурсов – больше выпуска.Из всевозможных производственных функций основное внимание уделяется функциям с неоклассическими свойствами:
1.  ; ;
2. Функция должна быть дважды дифференцируема;
3.  – предельный продукт фактора (MPF); – предельный продукт фактора (MPF);
4.  – убывающая отдача дополнительных затрат фактора. – убывающая отдача дополнительных затрат фактора.
ОДНОФАКТОРНАЯ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ.
Рассмотрим однофакторную производственную функцию при условии нехватки труда. Остальные условия мы берем неизменными. Исследуем, как будет увеличиваться выпуск продукции в зависимости от труда.

На графикеА – точка перегиба.Затраты от 0 до FA дают по сравнению с предыдущей большую отдачу. Вторая производная больше 0. После FA – постоянно уменьшающаяся отдача. В точке D полное насыщение производства. Это график стандартной технологии.
Условие задачи:Пусть:  – средний продукт (средняя производительность фактора) – средний продукт (средняя производительность фактора)
 ; ;  – показатель предельной производительности.МР показывает, насколько увеличится производство при затрате последней единицы фактора. – показатель предельной производительности.МР показывает, насколько увеличится производство при затрате последней единицы фактора.
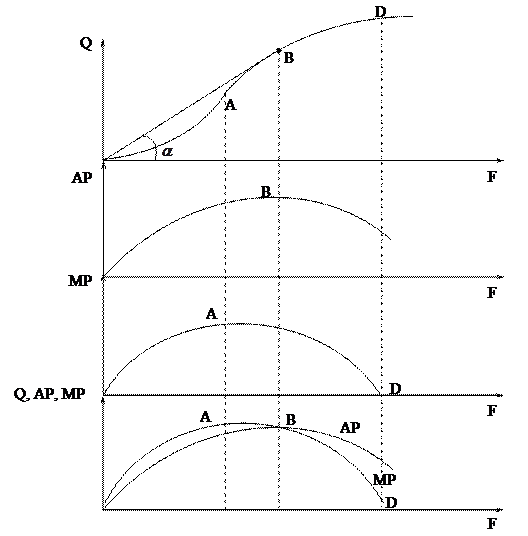 Пояснения к рисунку. Пояснения к рисунку.
Каждая единица фактора имеет разную отдачу. Показатель AP характеризует отдачу от всех затрат, но очень важно знать тенденцию, т.е. как будет изменяться выпуск в зависимости от каждой следующей единицы затрат фактора. Об этом нам говорит MP.
Рассмотрим характеристики стандартной технологии с точки зрения последовательных затрат фактора. На интервале (1) каждая последовательная единица фактора дает нам все большую отдачу, следовательно, предельная производительность растет, а с ней растет и AP, вплоть до точки А
На участке (2) каждая последующая единица дает все меньшую отдачу, но, тем не менее, отдача каждой следующей единицы все еще выше, чем средняя отдача всех предшествующих затрат, следовательно, АР растет, вплоть до точки В.
Отдача от дополнительной единицы факторов в точке В равна отдаче от всех предшествующих затрат, следовательно, АР = МР.На участке (3) каждая дополнительная единица фактора дает меньше отдачи, чем в среднем все предшествующие, поэтому понижение МР ведет к снижению АР до точки D. После точки D новые затраты фактора дают нулевой эффект.
Свойства графика:1)Максимальная отдача – в точке А.2)Максимальная средняя отдача – в точке В.3)Максимальный выпуск продукции – в точке D.
 – если затраты фактора увеличить в n раз.Мы анализируем «эффект масштаба производства». Нам надо сравнить n и m.Если затраты F увеличить в n раз, а производство увеличится меньше, чем в n раз (m<n), то имеем потери от масштаба. Если m>n, то имеем экономию от масштаба – положительный эффект масштаба производства. Оптимальные размеры производства с точки зрения технологии связаны с эффектом масштаба. Для стандартной технологии положительный эффект масштаба производства, оптимальный режим, дальнейшее расширение – потери от масштаба.ОДНОПРОДУКТОВАЯ ДВУХФАКТОРНАЯ МОДЕЛЬ.Нам необходимо рассмотреть эффекты взаимзаменяемости и взаимодополняемости факторов. Благодаря выводам, полученным при изучении двухфакторной модели, результаты этого изучения мы можем использовать для распространения на многофакторные модели. – если затраты фактора увеличить в n раз.Мы анализируем «эффект масштаба производства». Нам надо сравнить n и m.Если затраты F увеличить в n раз, а производство увеличится меньше, чем в n раз (m<n), то имеем потери от масштаба. Если m>n, то имеем экономию от масштаба – положительный эффект масштаба производства. Оптимальные размеры производства с точки зрения технологии связаны с эффектом масштаба. Для стандартной технологии положительный эффект масштаба производства, оптимальный режим, дальнейшее расширение – потери от масштаба.ОДНОПРОДУКТОВАЯ ДВУХФАКТОРНАЯ МОДЕЛЬ.Нам необходимо рассмотреть эффекты взаимзаменяемости и взаимодополняемости факторов. Благодаря выводам, полученным при изучении двухфакторной модели, результаты этого изучения мы можем использовать для распространения на многофакторные модели. 
Мы имеем дело с неоклассической функцией:
·  ; ;
·  ; ;
·  ; ;
Возможности взаимной замены факторов несколько ограничены.
 F (K0, L0) Þ Q0 – выпуск продукции в точке А. Q0 = const. Требуется найти все комбинации F при которых объем выпуска будет постоянен и равен Q0.Изокванта производственной функции – это геометрическое место всех комбинаций ресурсов, при которых выпуск продукции остается постоянным. F (K0, L0) Þ Q0 – выпуск продукции в точке А. Q0 = const. Требуется найти все комбинации F при которых объем выпуска будет постоянен и равен Q0.Изокванта производственной функции – это геометрическое место всех комбинаций ресурсов, при которых выпуск продукции остается постоянным.
Для данной технологии требуется рассмотреть все возможные значения выпуска в зависимости от затрат ресурсов.Получаем семейство изоквант для данной технологии. В идеале мы должны считать, что изокванты непрерывны. Для одной и той же технологии изокванты не пересекаются. Для неоклассической производственной функции изокванты не пересекают оси координат. Чем больше выпуск Q, тем изокванта дальше от начала координат. Если мы движемся по изокванте, мы можем рассмотреть возможности взаимной замены ресурсов при постоянном выпуске Q в условиях данной технологии.
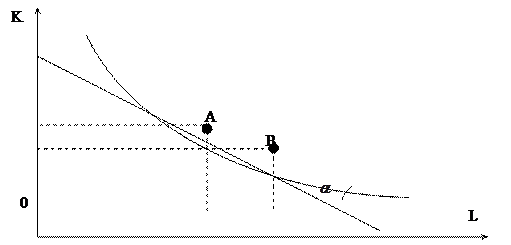

 – интервальная норма замещения. – интервальная норма замещения.
 – очень маленькое приращение в окрестностях одной точки. – очень маленькое приращение в окрестностях одной точки.
Предельная норма технического замещение (MRTS)показывает возможности замещения ресурсов в каждой точке.Показатель MRTS должен быть связан с МР:


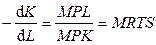
Виды изоквант:1)Ресурсы абсолютно взаимодополняемые – изокванта2)Ресурсы абсолютно взаимозаменяемы – изокванта 3)  Все остальные случаи (например, 3) промежуточные ситуации (изокванты неоклассических производственных функций). Все остальные случаи (например, 3) промежуточные ситуации (изокванты неоклассических производственных функций).
Для теории производства вид изокванты имеет большее значение. Поэтому важно найти характеристику, которая показывает степень изогнутости изокванты. Мы можем измерить эластичность взаимной замены факторов, а именно, соотношение факторов хотелось бы представить как функцию  .Эластичность этой функции будет показывать, на сколько процентов изменится K/L, если MRTS изменится на 1%. .Эластичность этой функции будет показывать, на сколько процентов изменится K/L, если MRTS изменится на 1%.

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , где a > 0, b < 1
, где a > 0, b < 1
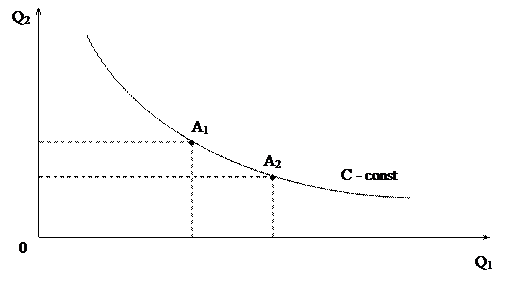 Общее положение: для описания поведения потребителя можно использовать особую функцию с перечисленными свойствами (неоклассическая функция потребления).Экономический смысл: мы рассматриваем пространство товаров, в котором мы можем рассмотреть различные уровни полезности (C – значение полезности). qi > 0 означает, что все товары необходимы. Свойство 2a показывает, как изменится полезность набора, если увеличить на единицу количество одного из благ – предельная полезность (Uj). В свойство 2b показывает: если в одном наборе мы последовательно наращиваем количество одного из благ, то предельная полезность уменьшается – закон Госсена.Отныне мы можем считать, что каждый потребитель имеет собственную функцию полезности. С помощью этой функции он может определить полезность любого уровня благ. Если C – число, то возвращаемся к количественному подходу. Если C нельзя определить до числа, то остаемся в рамках порядкового подхода. Количественный и порядковый подход не противоречивы.АНАЛИЗ КРИВЫХ БЕЗРАЗЛИЧИЯ:Требуется определить, как происходит эквивалентное замещение одного блага другим? Условие задачи:Пусть изменяется количество блага q1. Необходимо определить, насколько должно измениться количество q2, чтобы общая полезность набора не уменьшилась (q2 – ?).
Общее положение: для описания поведения потребителя можно использовать особую функцию с перечисленными свойствами (неоклассическая функция потребления).Экономический смысл: мы рассматриваем пространство товаров, в котором мы можем рассмотреть различные уровни полезности (C – значение полезности). qi > 0 означает, что все товары необходимы. Свойство 2a показывает, как изменится полезность набора, если увеличить на единицу количество одного из благ – предельная полезность (Uj). В свойство 2b показывает: если в одном наборе мы последовательно наращиваем количество одного из благ, то предельная полезность уменьшается – закон Госсена.Отныне мы можем считать, что каждый потребитель имеет собственную функцию полезности. С помощью этой функции он может определить полезность любого уровня благ. Если C – число, то возвращаемся к количественному подходу. Если C нельзя определить до числа, то остаемся в рамках порядкового подхода. Количественный и порядковый подход не противоречивы.АНАЛИЗ КРИВЫХ БЕЗРАЗЛИЧИЯ:Требуется определить, как происходит эквивалентное замещение одного блага другим? Условие задачи:Пусть изменяется количество блага q1. Необходимо определить, насколько должно измениться количество q2, чтобы общая полезность набора не уменьшилась (q2 – ?). – интервальная норма взаимной замены. Интервальная норма взаимной замены показывает, на сколько единиц нужно уменьшить потребление второго товара при увеличении первого товара на единицу при условии, что общая полезность неизменна. При последовательном увеличении количества одного и того же товара в наборе нам будет требоваться все меньшее количество второго товара для поддержания уровня полезности. Из этого следует два вывода:1)Ценность каждой единицы блага зависит от количества данного блага и от количества других благ, причем, чем больше данного блага в наборе, тем меньше ценность каждой последующей единицы и наоборот.2)Так как ценность благ существенно зависит от их количества, показатель интервальной нормы эквивалентной замены является очень грубым измерителем. Правильнее было бы измерять возможности эквивалентной замены благ в каждой точке кривой безразличия.
– интервальная норма взаимной замены. Интервальная норма взаимной замены показывает, на сколько единиц нужно уменьшить потребление второго товара при увеличении первого товара на единицу при условии, что общая полезность неизменна. При последовательном увеличении количества одного и того же товара в наборе нам будет требоваться все меньшее количество второго товара для поддержания уровня полезности. Из этого следует два вывода:1)Ценность каждой единицы блага зависит от количества данного блага и от количества других благ, причем, чем больше данного блага в наборе, тем меньше ценность каждой последующей единицы и наоборот.2)Так как ценность благ существенно зависит от их количества, показатель интервальной нормы эквивалентной замены является очень грубым измерителем. Правильнее было бы измерять возможности эквивалентной замены благ в каждой точке кривой безразличия.


 . Запишем условие полного расходования бюджета потребителя. Пусть потребитель приобрел набор q1 и q2.
. Запишем условие полного расходования бюджета потребителя. Пусть потребитель приобрел набор q1 и q2. 



 Если цены на товары неизменны, а R увеличится, бюджетная линия изменится, так что произойдет параллельный сдвиг прямой, угол останется тот же.СРАВНИТЕЛЬНАЯ СТАТИКА ПОТРЕБЛЕНИЯ.Существуют 2 модели:1)Статическая модель – исследуют по методу при прочих равных условиях. Такой метод называется сравнительная статика.2)Динамическая модель – при этом применяется несколько управляющих элементов. Исследование динамики – очень сложный вопрос.Условие задачи:Дана неоклассическая задача потребления, т.е. известны потребительские предпочтения, заданы потребительский бюджет и система цен. Определить оптимальный план закупок для данного потребителя
Если цены на товары неизменны, а R увеличится, бюджетная линия изменится, так что произойдет параллельный сдвиг прямой, угол останется тот же.СРАВНИТЕЛЬНАЯ СТАТИКА ПОТРЕБЛЕНИЯ.Существуют 2 модели:1)Статическая модель – исследуют по методу при прочих равных условиях. Такой метод называется сравнительная статика.2)Динамическая модель – при этом применяется несколько управляющих элементов. Исследование динамики – очень сложный вопрос.Условие задачи:Дана неоклассическая задача потребления, т.е. известны потребительские предпочтения, заданы потребительский бюджет и система цен. Определить оптимальный план закупок для данного потребителя – функция от (N+1) переменных.Спрос на отдельно взятый товар – функция от цен и дохода – это функция покупательского спроса.Метод сравнения статики заключается в следующем: берем один из аргументов, остальные считаем заданными:
– функция от (N+1) переменных.Спрос на отдельно взятый товар – функция от цен и дохода – это функция покупательского спроса.Метод сравнения статики заключается в следующем: берем один из аргументов, остальные считаем заданными:  .Рассмотрим влияние изменения дохода на покупательский спрос
.Рассмотрим влияние изменения дохода на покупательский спрос  .
.



 ;
; ;
; – предельный продукт фактора (MPF);
– предельный продукт фактора (MPF); – убывающая отдача дополнительных затрат фактора.
– убывающая отдача дополнительных затрат фактора.

 – средний продукт (средняя производительность фактора)
– средний продукт (средняя производительность фактора) ;
;  – показатель предельной производительности.МР показывает, насколько увеличится производство при затрате последней единицы фактора.
– показатель предельной производительности.МР показывает, насколько увеличится производство при затрате последней единицы фактора.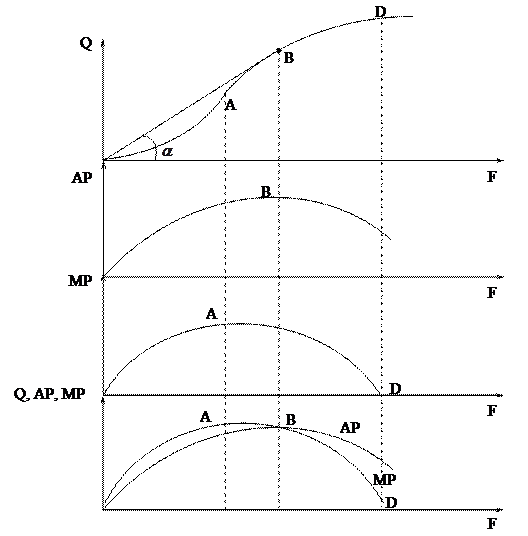 Пояснения к рисунку.
Пояснения к рисунку. – если затраты фактора увеличить в n раз.Мы анализируем «эффект масштаба производства». Нам надо сравнить n и m.Если затраты F увеличить в n раз, а производство увеличится меньше, чем в n раз (m<n), то имеем потери от масштаба. Если m>n, то имеем экономию от масштаба – положительный эффект масштаба производства. Оптимальные размеры производства с точки зрения технологии связаны с эффектом масштаба. Для стандартной технологии положительный эффект масштаба производства, оптимальный режим, дальнейшее расширение – потери от масштаба.ОДНОПРОДУКТОВАЯ ДВУХФАКТОРНАЯ МОДЕЛЬ.Нам необходимо рассмотреть эффекты взаимзаменяемости и взаимодополняемости факторов. Благодаря выводам, полученным при изучении двухфакторной модели, результаты этого изучения мы можем использовать для распространения на многофакторные модели.
– если затраты фактора увеличить в n раз.Мы анализируем «эффект масштаба производства». Нам надо сравнить n и m.Если затраты F увеличить в n раз, а производство увеличится меньше, чем в n раз (m<n), то имеем потери от масштаба. Если m>n, то имеем экономию от масштаба – положительный эффект масштаба производства. Оптимальные размеры производства с точки зрения технологии связаны с эффектом масштаба. Для стандартной технологии положительный эффект масштаба производства, оптимальный режим, дальнейшее расширение – потери от масштаба.ОДНОПРОДУКТОВАЯ ДВУХФАКТОРНАЯ МОДЕЛЬ.Нам необходимо рассмотреть эффекты взаимзаменяемости и взаимодополняемости факторов. Благодаря выводам, полученным при изучении двухфакторной модели, результаты этого изучения мы можем использовать для распространения на многофакторные модели. 
 ;
; ;
; ;
;
 F (K0, L0) Þ Q0 – выпуск продукции в точке А. Q0 = const. Требуется найти все комбинации F при которых объем выпуска будет постоянен и равен Q0.Изокванта производственной функции – это геометрическое место всех комбинаций ресурсов, при которых выпуск продукции остается постоянным.
F (K0, L0) Þ Q0 – выпуск продукции в точке А. Q0 = const. Требуется найти все комбинации F при которых объем выпуска будет постоянен и равен Q0.Изокванта производственной функции – это геометрическое место всех комбинаций ресурсов, при которых выпуск продукции остается постоянным.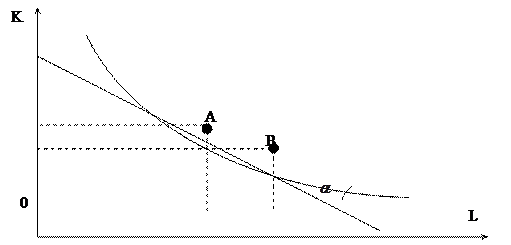

 – интервальная норма замещения.
– интервальная норма замещения. – очень маленькое приращение в окрестностях одной точки.
– очень маленькое приращение в окрестностях одной точки.
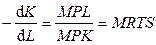
 Все остальные случаи (например, 3) промежуточные ситуации (изокванты неоклассических производственных функций).
Все остальные случаи (например, 3) промежуточные ситуации (изокванты неоклассических производственных функций). .Эластичность этой функции будет показывать, на сколько процентов изменится K/L, если MRTS изменится на 1%.
.Эластичность этой функции будет показывать, на сколько процентов изменится K/L, если MRTS изменится на 1%.