
|
|
Логическое следование и равносильность формул. Связь с булевыми алгебрами.
3.1. Логическое следование и равносильность формул.Пусть А и В — произвольные формулы логики высказываний. Определение 6. Если формула А®В является тавтологией, то говорят, что из формулы А логически следует формула В, или говорят, что Вявляется логическим следствиемА. В этом случае пишут А ÞВ. Если же формула А«В является тавтологией, то говорят, что формулы А иВлогически эквивалентны или просто эквивалентны. Пишут АÛВ или А~В. Мы будем придерживаться второго обозначения Из этого определения вытекает следующее утверждение: если из формулы А логически следует формула В и из формулы Влогически следует формула А, то формулы Аи В логически эквивалентны, и обратно. Это утверждение легко доказать с помощью тавтологии: (а®b)&(b®а)«(а«b) в которой пропозициональную переменную а следует заменить формулой А, и переменную b— формулой В. Упражнение 3.1. Доказать, что имеют место следующие логические следствия: а) АÞA; б) (А®В)&(В®С))Þ(А®C); в) А®ВÞ(В®С)®(А®C); г) (А®В)®CÞ(А®В)®(А®C); д) А®(В ®C) Þ В ®(А® C); е)А®ВÞØВ®ØА; ж) ØАÞА®В; з)А«ВÞА®В; и) (А«В)&(А«C)ÞА«C; к) (А&В)®CÞА®(В®C); л) А®(В®C)Þ(А&В)®C; м)А®ВÞ(АÚС)®(ВÚС); н) А®ВÞ(А&С)®(В&С). Решение. б) Так как формула (a®b)&(b®c))®(a®c) является тавтологией (см. §2, тавтология 2)), то согласно определения логического следования данное следование имеет место. Упражнение 3.2. Используя определение и тавтологии из §2, установите следующие равносильности: а) А&В~В&А (коммутативность конъюнкции); б) АÚВ~ВÚА (коммутативность дизъюнкции); в) (А&В)&C~А&(В&C) (ассоциативность конъюнкции); г) (АÚВ)ÚC~АÚ(ВÚC) (ассоциативность дизъюнкции); д) А&(ВÚC)~(А&В)Ú(А&C) (дистрибутивность конъюнкции относительно дизъюнкции); е) АÚ(В&C)~(АÚВ)&(АÚC) (дистрибутивность дизъюнкции относительно конъюнкции); ж) А&А~А (идемпотентность конъюнкции); з) АÚА~А (идемпотентность дизъюнкции); и) А&ØА~0(закон противоречия); к) АÚ0~А, А&0~0; л) АÚØА~ 1(закон исключённого третьего); м) АÚ1~1, А&1~А; н) А&(ВÚА)~А (законы о) АÚ(В&А)~А поглощения); п) А®В~ØАÚВ; р) Ø(А&В)~ØАÚØВ (законы ; с) Ø(АÚВ)~ØА&ØВ де Моргана; т) А«В~(А®В)&(В®А); у) ØØА~А (закон снятия двойного отрицания). Как видим, операции & и Ú обладают свойствами коммутативности (а) и б)), ассоциативности ((в) и г)), дистрибутивности относительно друг друга (д) и е)), идемпотентности (ж) и з)). Свойства и) и к) носят название законов нуля, при этом свойство и) называется также законом противоречия. Свойства л) и м) - законы единицы, при этом закон л) называется также законом исключённого третьего. Свойства н) и о) - законы поглощения. Свойства р) и с) - законы де Моргана. Свойство у) - закон снятия двойного отрицания. Очевидно, эти свойства естественным образом обобщаются. Например, свойство а) обобщается на произвольное число конъюнкций: a&b&c~a&c&b~b&a&c и т.д. Кстати, возможность опускать скобки вытекает из в). Вообще, в конъюнкции вида (…((a1&a2)&a3)&…&an) скобки можно проставлять произвольным образом, то есть результат не зависит от расстановки скобок. В силу этого в такого рода конъюнкциях скобки не ставятся. Всё сказанное распространяется и на дизъюнкции. Далее, д) и е) имеют естественные обобщения: а&(b1Úb2Ú…Úbk)~a&b1Úa&b2Ú…Úa&bk, аÚ(b1&b2&…&bk)~(aÚb1)&(aÚb2)&… &(aÚbk). И т.д. Используя равносильности 3.2 их следствия, можно формулу или её подформулу заменить равносильной ей. Это означает, что если А Равносильные преобразования используются для доказательства равносильностей, для приведения формул к заданному виду, в частности, для упрощения формул. Формула А считается проще равносильной ей формулы В, если она содержит меньше букв (по вхождению или наименованию) и меньше логических операций. При этом операции эквивалентность, импликация, штрих Шеффера, стрелка Пирса и логическое сложение заменяются операциями конъюнкции и дизъюнкции, а отрицание относят к пропозициональным переменным (к элементарным высказываниям). Упражнение 3.3. С помощью равносильных преобразований доказать следующие равносильности. а) (хÚу)&(хÚØу)~x; б) хÚ(Øх&y)~хÚу; в) х«у~Øх«Øу; г) (х&у)Ú(Øх&у)Ú(Øх&Øу)~х®у; д) х®Øу~y®Øx; е) х®(y®z)~ х&y®z; ж) х~(х&y&z)Ú(х&y&Øz)Ú(x&Øу&z)Ú(х&Øу&z); з) (хÚy)&(zÚt)~(х&z)Ú(y&z)Ú(x&t)Ú(y&t); и) (х&y)Ú(z&t)~(хÚz)&(yÚz)&(xÚt)&(yÚt). Решение. 1. (хÚу)&(хÚØу) á(1) Воспользовались дистрибутивностью Ú относительно &. (2) Воспользовались законом противоречия. (3) Воспользовались одним из законов нуля.ñ Упражнение 3.4. Упростить формулы: а) х®(x®x); б) х®(х®у); в) Ø(Øх&Øу)Ú(х®у)&x; г)(х«у)&(хÚу); д) (х®у)&(у®z)®(z®x); е) (х®у)&(у®z)®(х®z); ж) (xÚy)«(y¯ з) (x| Решение. в) Ø(Øх&Øу)Ú(х®у)&x á(1) Воспользовались законом де Моргана и равносильностью п) упражнения 3.2. (2) Воспользовались законом снятия двойного отрицания и дистрибутивностью & относительно Ú. (3) Воспользовались законом противоречия. (4) Воспользовались одним из законов нуля. (5) Воспользовались ассоциативностью операции Ú. (6) Воспользовались законом поглощения.ñ 3.2. Связь с булевыми алгебрами. Если между формулами установить отношение равенства «=» по правилу А=В Û А~В, то на множестве B высказываний определяется алгебра áB; &, Ú; Ø; 0, 1ñ, которая является булевой. Это следует из свойств операций &, Ú, рассмотренных в упражнении 3.2. Эта алгебра изоморфна некоторой алгебре Кантора áP(U); Ç, È; Пример 3.1. Проверим с помощью алгебры логики тождества: а) (АÈВ)\(СÇА)=(В\С)\(АÈС); б) А\(В\С)=(А\В)È(АÇС). а) Переведём сначала правую и левую части на язык алгебры логики. При этом А, В и С соответствуют a, b и c соответственно: (АÈВ)\(СÇА)®(aÚb)&
б) А\(В\С)®a& Имеем a& то есть a& Ясно, что операции кольцевой суммы в алгебре логики и теории множеств соответствуют друг другу. В частности, алгебра áB; &, Åñ - ассоциативное, коммутативное кольцо с единицей. Оно, как известно, является булевым (см. Часть II). В частности, это означает, что кроме перечисленных выше эквивалентностей имеют место следующие: 1) аÅb~bÅa; 2) (aÅb)Åc~aÅ(bÅc); 3) aÅ0~a; 4) a&(bÅc)~(a&b)Å(a&c). Кроме того, этот список можно продолжить: 5) aÚb~aÅbÅ(a&b); 6) 7) aÅ Доказательство этих равенств предлагается провести в качестве упражнения 3.5.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 В - некоторая формула, где
В - некоторая формула, где  хÚ(у&Øу)
хÚ(у&Øу)  хÚ0
хÚ0 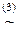 x
x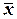 );
); )®(zÅ
)®(zÅ  .
.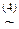 (хÚу)Ú(у&x)
(хÚу)Ú(у&x) 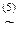 хÚ(уÚ(у&x))
хÚ(уÚ(у&x))  хÚу.
хÚу. ; Æ, Uñ (определение алгебры Кантора см. в Части II). Не вдаваясь в подробности отметим только, что если j - этот изоморфизм, то j(a&b)=j(a)Çj(b), j(aÚb)=j(a)Èj(b), j(Øa)=
; Æ, Uñ (определение алгебры Кантора см. в Части II). Не вдаваясь в подробности отметим только, что если j - этот изоморфизм, то j(a&b)=j(a)Çj(b), j(aÚb)=j(a)Èj(b), j(Øa)=  , j(0)=Æ, j(1)=U и др. В частности, j(a&
, j(0)=Æ, j(1)=U и др. В частности, j(a&  )=j(a)Ç
)=j(a)Ç  =j(a)\j(b). Отсюда следует, что понятия и факты, связанные с алгеброй высказываний, можно соответствующим образом переносить на множества и обратно. Например, тождества теории множеств можно доказывать или опровергать на языке алгебры логики.
=j(a)\j(b). Отсюда следует, что понятия и факты, связанные с алгеброй высказываний, можно соответствующим образом переносить на множества и обратно. Например, тождества теории множеств можно доказывать или опровергать на языке алгебры логики. , (В\С)\(АÈС)®(b&
, (В\С)\(АÈС)®(b&  )&
)&  . Осталось показать, что (aÚb)&
. Осталось показать, что (aÚb)& 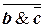 , (А\В)È(АÇС)®(a&
, (А\В)È(АÇС)®(a&  ~aÅ1;
~aÅ1;