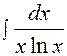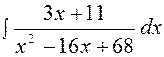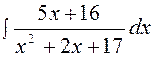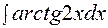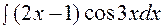|
|
Решение типовых примеров для контрольной работы № 2Содержание ВВЕДЕНИЕ.. 4 Решение типовых примеров для контрольной работы № 1. 5 Задания к контрольной работе № 1. 10 Решение типовых примеров для контрольной работы № 2. 21 Задания к контрольной работе № 2. 24 Теоретические вопросы.. 29 Приложение.. 31
ВВЕДЕНИЕ Настоящее пособие предназначено для студентов дистанционного обучения. Пособие содержит образцы решения задач, задания для контрольных работ, теоретические вопросы, справочные материалы и список литературы. При выполнении контрольных работ следует руководствоваться следующими указаниями. 1. Каждую работу следует выполнять в отдельной ученической тетради в клетку, на обложке которой должны быть указаны фамилия и инициалы студентов, номер зачетной книжки (шифр), номер контрольной работы. Решения всех задач и пояснения к ним должны быть подробными. Все вычисления (в том числе и вспомогательные) необходимо делать полностью. Чертежи и графики должны быть выполнены аккуратно и четко с указанием масштаба, координатных осей и других элементов чертежа. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже. 2. За учебный год студент должен выполнить две контрольные работы, состоящие из решения заданий и написания теоретических вопросов. Вариант для заданий выбирается в соответствии с двумя последними цифрами номера зачетной книжки студента. Распределение заданий приводится в таблицах 1 и 2 данных методических указаний. За первый семестр выполняется контрольная работа № 1, включающая три задания (вариант см. в табл. № 1) и ответ на теоретические вопросы с 1 по 11 (см. стр. 29-30) письменно. За второй семестр – контрольная работа № 2, включающая четыре задания (вариант см. в табл. № 2) и ответ на теоретические вопросы с 12 по 28 (см. стр. 29-30) письменно. 3. Если работа не зачтена, она возвращается студенту. Студент должен в кратчайшие сроки исправить в ней все отмеченные рецензентом недостатки и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
Решение типовых примеров для контрольной работы № 1 Задание № 1 Вычислить пределы 1) 3) Решение. 1) 2) ax2 + bx + c = a(x – x1)∙(x – x1), где х1, х2 – корни квадратного трехчлена ax2 + bx + c. У нас Теперь условие примера можно переписать в другом виде и продолжить решение:
3) Здесь сталкиваемся с неопределенностью
4) В данном случае для освобождения от неопределенности будем использовать первый замечательный предел и одно из его очевидных следствий:
Решение примера будет выглядеть следующим образом:
Задание № 2 Найти производные функций 1) 3) При решении всех последующих примеров на нахождение производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции: а) б) в) г) если задана сложная функция y = f(u), где u = j(x), то есть y = f(j(х)); если каждая из функций y = f(u) и u = j(x) дифференцируема по своему аргументу, то
Решение. 1)
2)
3)
4)
Задание № 3 Исследовать функцию и построить график
Решение. 1) Областью определения данной функции являются все действительные значения аргумента х,то есть D(y): 2) Исследуем функцию на интервалы монотонности и экстремумы. С этой целью найдем ее производную и приравняем нулю:
Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода х1= - 5, х2= - 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:
3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:
Итак, функция имеет одну критическую точку 2 рода
Значение х = - 3 является абсциссой точки перегиба графика функции, а ордината этой точки
4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты y = kx+b воспользуемся формулами
Таким образом, у графика заданной функции наклонных асимптот нет. 5) Для построения графика изобразим точки максимума А1( - 5; 4), минимума А2( - 1 - 4), перегиба А3(-3; 0) и точку А4(0; С учетом результатов предыдущих исследований построим кривую (см. рис. 1).
Рисунок 1 – Построение графика функции Задания к контрольной работе № 1 Задание 1 Найти указанные пределы:
Задание № 2 Найти производные, пользуясь правилами и формулами дифференцирования:
Задание № 3 Исследовать заданные функции методами дифференциального исчисления, начертить их графики.
Таблица 1 – Распределение заданий для контрольной работы № 1
Решение типовых примеров для контрольной работы № 2 Задание № 1 1. Найти неопределенный интеграл Решение. Применим подстановку
2. Найти интеграл Решение. Применим подставку t=3x3 – 5. Тогда
Задание № 2 Найти интеграл Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом: x2 – 6x+13 = x2 – 6x + 9 + 4 = (x - 3)2 + 22. Тогда после подстановки t = x - 3 получаем
Итак, учитывая, что t = x – 3, имеем
Задание № 3 1. Найти интеграл Решение. Применим формулу интегрирования по частям
Положим u = 3x+7, dv = cos5xdx, тогда du = 3dx, Следовательно,
2. Найти интеграл Решение. Положим u = arctg4x, dv = dx, тогда
Отсюда
Применяя в последнем интеграле подстановку t = 1+16x2, получаем,
Отсюда Задание № 4 Вычислить площадь, ограниченную параболами y = 2x2 – x – 2, y = - x2 + x – 1. Решение.
Рисунок 2 – График построения парабол
Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений: 2x2 – x – 2 = - x2 + x – 1. Отсюда 3x2 – 2x – 1 = 0, D = 4 + 4∙3 = 16,
Вычисление площади осуществляем по формуле:
где f1(x), f2(x) – кривые, ограничивающие фигуру (f2(x) ³ f1(x)). В нашем случае
Задания к контрольной работе № 2 Задание №1 Найти неопределенные интегралы способом подстановки (методом замены переменной)
Задание №2 Найти неопределенные интегралы, используя выделение полного квадрата
Задание № 3 Найти неопределенные интегралы, используя метод интегрирования по частям
Задание № 4 Вычислить площадь, ограниченную заданными параболами
Таблица 2 – Распределение заданий для контрольной работы № 2
Теоретические вопросы 1. Понятие предела функции в точке и в бесконечности. 2. Основные теоремы о пределах. Раскрытие неопределенностей при вычислении пределов. 3. Непрерывность функции в точке и на интервале. 4. Определение производной, ее геометрический смысл. 5. Правила вычисления производной. Таблица производных. 6. Исследование функции на интервалы монотонности. Точки экстремума. 7. Исследование функции на интервалы выпуклости. Точки перегиба. 8. Асимптоты кривой. 9. Общая схема исследования функции. 10. Дифференциал функции. 11. Применение дифференциала к приближенным вычислениям. 12. Первообразная функции и неопределенный интеграл. 13. Правила вычисления неопределенного интеграла. Таблица интегралов. 14. Методы вычисления неопределенного интеграла. 15. Определенный интеграл. Формула Ньютона-Лейбница. 16. Основные свойства определенных интегралов. 17. Методы вычисления определенного интеграла. 18. Вычисление площадей плоских фигур. 19. Основные понятия теории вероятностей: события, вероятность события, частота события, случайная величина. 20. Сумма и произведение событий, теоремы сложения и умножения вероятностей. 21. Дискретные случайные величины. Ряд, многоугольник и функция распределения. 22. Непрерывные случайные величины. Функция и плотность распределения. 23. Формула полной вероятности. 24. Числовые характеристики случайных величин: дисперсия; и среднеквадратичное отклонение. 25. Понятия: группа, выборка, генеральная совокупность. 26. Эмпирическая функция распределения. 27. Вариационный ряд. Полигон частот и гистограмма 28. Точечные оценки. Выборочная средняя и выборочная дисперсия. Приложение
Правила дифференцирования:
Производная сложной функции:
Таблица производных основных элементарных функций и производных сложных функций 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;2)
;2)  ,
, ,4)
,4)  .
. .
. ,при подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида
,при подстановке вместо переменной х ее предельного значения 3 получается неопределенность вида  . Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой
. Для избавления от этого типа неопределенности в нашем случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой , так как дискриминант квадратного трехчлена
, так как дискриминант квадратного трехчлена  а следовательно, х1 = 3,
а следовательно, х1 = 3,  . Аналогично x2 – x – 6 = (x - 3)∙(x + 2).
. Аналогично x2 – x – 6 = (x - 3)∙(x + 2). ;
; .
. , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной:
, избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной: ;
; ;
;  .
.
 ; 2)
; 2)  ;
;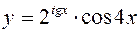 ; 4)
; 4)  .
. ;
; ;
;







 ;
;

 ;
;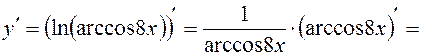

 .
. .
. а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.
а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот. .
.





 .
. .
.




 .
. .
. .
. ).пересечения графика с осью Оу .
).пересечения графика с осью Оу .








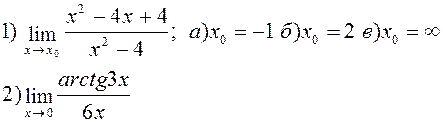























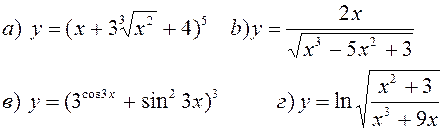


























































 , тогда
, тогда  и
и ;
; .
. ;
; 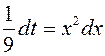 , откуда
, откуда .
.
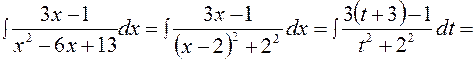

 причем, при вычислении интеграла
причем, при вычислении интеграла  воспользуемся заменой переменной z = t2+4, тогда dz = 2tdt, откуда
воспользуемся заменой переменной z = t2+4, тогда dz = 2tdt, откуда .
.
 .
. .
.
 .
.
 .
. .
. v = x.
v = x. .
. , следовательно,
, следовательно, .
. .
.
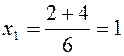 ,
, 
 ,
,