
|
|
Определение давлений в шарнирахРАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе по дисциплине «Теория Механизмов и Машин» (Номер задания 215)
Выполнил: Студент гр.1309 Кильмаков Н.М. Проверил: Профессор Яруллин М.Г.
Казань 2014
Оглавление 1. Исследование шарнирно – рычажного шестизвенного механизма……………..3 1.1 Исходные данные………………………………………………………………….3 1.2 Построение кинематической схемы и структурный анализ механизма………4 1.3 Определение скоростей…………………………………………………………...5 1.4 Определение ускорений…………………………………………………………..8 1.5 Силовой анализ механизма……………………………………………………...11 1.5.1 Определение давлений в шарнирах…………………………………………..11 1.5.2 Определение момента, приложенного к кривошипу………………………..14 1.5.3 Определение момента методом рычага Жуковского………………………..14 1.5.4 Расчет относительной погрешности………………………………………….15
1.1 Исходные данные…………………………………………………………………………………………………………………c.9 1.2 Определение геометрических параметров зубчатого колеса……………………c.9 1.3 Определение геометрических параметров зубчатого зацепления…..……..c.10 1.4 Определение качественных характеристик зубчатого зацепления……….c.11
Исследование шарнирно-рычажного шестизвенного механизма Исходные данные LOA=0.25м; LAB=1.0м; LBE=0.15м; LEC=1.1м
Построение кинематической схемы и структурный анализ механизма Определение скоростей Величина скорости точки А определяется по формуле VА = ω1⋅ lОА, м/с, где lОА = KL ⋅ ОА – длина кривошипа, м; ОА – отрезок на чертеже, изображающий в масштабе KL длину кривошипа, мм; а направление – в соответствии с направлением ω1 (перпендикулярно ОА). Для определения скорости точки В составим векторное уравнение:
В этом уравнении известны величина и направление вектора В этом уравнении два неизвестных элемента: величина скорости VB и VBA. А так как векторное уравнение соответствует двум скалярным, то указанное уравнение имеет определенное решение. Для определения этих неизвестных строим многоугольник (план) скоростей. По указанному в задании отрезку оа, изображающему на чертеже скорость VA, подсчитываем масштаб скорости: KV = VA/oa, м/(с⋅мм) (оа =70 мм). Из произвольно взятой на чертеже точки "о" откладываем отрезок оа перпендикулярно ОА. Через конец этого отрезка (точку а) проводим прямую перпендикулярно АВ, а через точку "о" – прямую, параллельную OY. Полученная от пересечения этих прямых точка b определяет длины отрезков оb и аb, которые изображают на чертеже скорости VB и VBA. Величины этих скоростей: VB = ob⋅KV, м/с; VBA = ab⋅KV, м/с.Для определения скорости точки C составим два уравнения:
и решим их совместно. Для чего через точку a проведем прямую перпендикулярно AE и через точку b – прямую перпендикулярно EB. Пересечение этих прямых определяет точку e, отрезок oe и, следовательно, скорость VE, численное значение которой VE = oe⋅KV, м/с. Для определения скорости точки C составим векторное уравнение:
В этом уравнении известны величина и направление вектора В этом уравнении два неизвестных элемента: величина скорости VC и VCE. Из точки "e" проводим прямую перпендикулярно СE, а через точку "о" – прямую, перпендикулярную OC. Полученная от пересечения этих прямых точка" c" определяет длины отрезков ос и cе, которые изображают на чертеже скорости VC и VCE. Величины этих скоростей: VC = oc⋅KV, м/с; VCE = ce⋅KV, м/с. Скорость точки S4 определяется из уравнения:
В этом уравнении известны величина и направление вектора В этом уравнении неизвестный элемент: величина скорости VS4. Из точки "e" проводим VS4 = os4⋅KV, м/с; Для определения скорости точки S2 составим два уравнения: VS2 =VA+VS2A, VS2 =VB+VS2B, и решим их совместно. Для чего через точку a проведем прямую перпендикулярно S2C и через точку b – прямую перпендикулярно S2B. Пересечение этих прямых определяет точку S2, отрезок os2 и, следовательно, скорость VS4, численное значение которой VS2 = os2⋅KV, м/с. Теперь найдем угловые скорости звеньев.Угловая скорость шатуна 2: ω2 = VBA / lAB, 1/c, где lAB = KL⋅ AB – длина шатуна 1м; Угловая скорость шатуна 4: ω4 = VCE / lCE, 1/c, где lCE = KL⋅ СE – длина шатуна 1.1м; На примере 9-го положения: VA=w1*LOA =35*0,25=8,75 (м/с) Kv=VA/oa=8,75/70=0,125 (м/(с*мм)) VB=VA+VBA VB=ob*Kv =27,36*0,125=3,42 (м/с) VBA=ab*Kv=61,1*0,125=7,62 (м/с) VD=od*Kv=29,92*0,125=3,74 (м/с) VDA=ad*Kv=*0,125= (м/с) VC=oc*Kv=34,98*0,125=4,3725 (м/с) VCD=cd*Kv=5,79*0,125=07238 (м/с) VS4=os4*KV=2,89*0,0714=4.336 (м/с) VS2 = as2⋅KV=36,66*0,125=4,5825 (м/с) ω2=VBA/LAB=7,62 /1=7,62 (1/c) ω4=VCD/LCD=0,7238/1.1=0,6581 (1/c) ω5=VC/LOC=4,3725 /0.7=6,25 (1/c) Результаты расчета скоростей для 12-ти положений приведены в (Табл.1). Таблица 1
Определение ускорений Перейдем теперь к определению ускорений. Ускорение точки А определяется по формуле
(так как ω1=const и ε1=0) и направлено от точки А к точке О. Ускорение точки B находится из уравнения
где В этом уравнении , м/с2 Для решения уравнения из произвольно взятой точки "о" проводим вектор с его конца строим вектор
Длины отрезков соответствующие ускорениям
где Kа – произвольно взятый масштаб ускорения, м/(с2*мм)
В полученной точке пересечения прямых будет точка "b". Где будут концы векторов изображающие скорости Численное значение этих ускорений
Угловое ускорение 2 звена находится по формуле
Для установления направления ε2 и перенесем ускорения Ускорение точки Е находим из уравнений
где Значение ускорений
Длины отрезков соответствующие ускорениям
Для решения уравнения из точки "о" проводим вектор
Для определения ускорения точки C, принадлежащей звену 4 составим уравнение, так как точка С принадлежит звену 4 и 5, то уравнение выглядит следующим образом
где
где Значение ускорений , м/с2
Длины отрезков, соответствующие ускорениям
Окончательный вид уравнения будет следующим:
В этом уравнение неизвестны лишь значения двух ускорений Для решаем уравнение графическим способом. Из точки "а" проводим отрезок Численное значение
Угловое ускорение 4 и (условно)5 звеньев находятся по формуле
Ускорение точки центра масс второго и четвертого звеньев находятся по следующим формулам
Все части уравнения уже известны.
Длины отрезков, соответствующие ускорениям
Из точки "а" проводим отрезок
Из точки "е" проводим отрезок
Результаты расчета ускорений для 2 и 6 положения приведены в (Табл.2). Таблица 2
Силовой анализ механизма Для силового анализа необходимо следующее: кинематическое исследование (определение скоростей и ускорений характерных точек механизма, включая центров масс звеньев, а также угловых скоростей и угловых ускорений звеньев) которого должно быть проведено заранее. Известны массы (mi) и моменты инерции (Ii) * звеньев. Требуется определить силы, приложенные к звеньям. Силами трения пренебрегаем. При отсутствии сил трения сила, с которой одно звено действует на другое, всегда направлена по нормали к поверхности их касания. Так, для вращательной пары эта сила проходит через центр вращательной пары (центр шарнира), для поступательной – перпендикулярно направляющей поступательной пары. При силовом исследовании механизм расчленяется на звенья (группы звеньев) и силовой расчет начинается с последнего звена, а заканчивается входным звеном (кривошипом 1), т. е. обратно порядку кинематического исследования. Определение давлений в шарнирах Итак, рассмотрим звено 4. На это звено действует шатун с силой Q4E, которая приложена в шарнире E, и ползун с силой N5C, приложенной к точке C, кроме того, к звену и шатуну приложены силы тяжести G4 и G5. Все эти силы можно заменить равнодействующей. Величина ее определяется по формуле
где Линия действия R4 параллельна ускорению где Линия действия R5 параллельна ускорению При этом
На основании теоремы Вариньона запишем относительно точки Е (центра шарнира) уравнение моментов сил, приложенных к звену 4, считая моменты, действующие против часовой стрелки, положительными:
Отсюда Отрицательное значение Из уравнения
графическим способом найдем силу точки "о" отложим в произвольном масштабе силы K, H/мм, равнодействующую R4 в виде вектора
С конца вектора откладываем равнодействующую R5
из той же точки "о" отложим вектор изображающий в том же масштабе силу G4, к концу её прибавим вектор
К концу вектора
Затем соединив конца векторов Численной значение равно
После этого рассмотрим звенья 2. На это звено действует кривошип с силой Q2А, которая приложена в шарнире А, и ползун с силой N3В, приложенной к точке В, кроме того, к звену и шатуну приложены силы тяжести G2 и G3. В точке Е на звено действует шатун с силой Q2E
Равнодействующие сил, приложенных к этим звеньям
Линия действия R2 параллельна ускорению Линия действия R3 параллельна ускорению На основании теоремы Вариньона запишем относительно точки А (центра шарнира) уравнение моментов сил, приложенных к звену 2, считая моменты, действующие против часовой стрелки, положительными:
Отсюда
Отрицательное значение Из уравнения
графическим способом найдем силу равнодействующую R2 в виде вектора
С конца вектора откладываем равнодействующую R3
из той же точки "о" отложим вектор изображающий в том же масштабе силу G2, к концу её прибавим вектор
К концу вектора
К концу вектора
Затем соединив конца векторов Численное значение равно

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 1=35 рад/с
1=35 рад/с
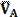 , а также направления векторов
, а также направления векторов  ( ||OY) и
( ||OY) и  (⊥ АВ).
(⊥ АВ).


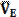 , а также направления векторов
, а также направления векторов  (⊥OC) и
(⊥OC) и  (⊥ CE).
(⊥ CE).
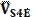 , а также направление вектора
, а также направление вектора  , м/с2,
, м/с2,
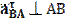

 получено выше, а
получено выше, а 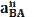 находится по формуле
находится по формуле ,
,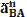 , а с его конца строим прямую перпендикулярную к АВ, а точки "о" проводим прямую параллельную OY
, а с его конца строим прямую перпендикулярную к АВ, а точки "о" проводим прямую параллельную OY находят по следующей формуле
находят по следующей формуле , мм
, мм , мм
, мм
 и
и  .
.

 , 1/c2
, 1/c2 в точку В и, рассматривая движение В относительно точек А, установим, что ε2 направлено против часовой стрелки.
в точку В и, рассматривая движение В относительно точек А, установим, что ε2 направлено против часовой стрелки.
 ∥АВ
∥АВ 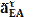 ⏊АВ
⏊АВ
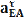 находятся по формулам
находятся по формулам
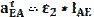
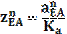

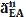 ,с его конца строим
,с его конца строим  ,на его конце получим точку "е". Сумма всех трёх векторов дает вектор
,на его конце получим точку "е". Сумма всех трёх векторов дает вектор 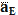 ,начало которого в точке "о", а конец в точке "е".
,начало которого в точке "о", а конец в точке "е".
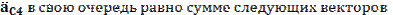

 складывается из нормального
складывается из нормального  и тангенсального ускорения
и тангенсального ускорения  т.е.
т.е.


 также двигается по своей окружности и, поэтому ускорения так же будет иметь нормальную и тангенсальную составляющую
также двигается по своей окружности и, поэтому ускорения так же будет иметь нормальную и тангенсальную составляющую



 находятся по формулам
находятся по формулам , м/с2
, м/с2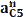 ,находятся по следующим формулам
,находятся по следующим формулам , мм
, мм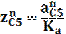 , мм
, мм

 , равный
, равный 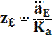 , мм., на его конце будет точка "е". Из точки "е" откладываем отрезок
, мм., на его конце будет точка "е". Из точки "е" откладываем отрезок  , с его конца проводим прямую перпендикулярную CE. Далее из точки "о" проводим отрезок
, с его конца проводим прямую перпендикулярную CE. Далее из точки "о" проводим отрезок  на его конце проводим прямую перпендикулярную OC. В точке пересечения прямых получим точку С. Полученные отрезки будут соответствовать длинам ускорений
на его конце проводим прямую перпендикулярную OC. В точке пересечения прямых получим точку С. Полученные отрезки будут соответствовать длинам ускорений  и
и 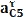
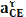 и
и  будет равно
будет равно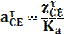 , м/с2
, м/с2 , м/с2
, м/с2 , 1/c2
, 1/c2 , 1/c2
, 1/c2
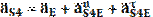
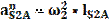 , м/с2
, м/с2 , м/с2
, м/с2 , м/с2
, м/с2 , м/с2
, м/с2


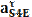 находятся по следующим формулам
находятся по следующим формулам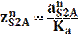 , мм
, мм , мм
, мм , мм
, мм , мм
, мм ,а с его конца отрезок
,а с его конца отрезок  .На конце последнего отрезка будет находится точка s2. Отрезок os2 будет соответствовать вектору ускорения
.На конце последнего отрезка будет находится точка s2. Отрезок os2 будет соответствовать вектору ускорения 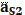 .Его численное значение будет равно
.Его численное значение будет равно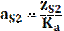 , м/с2
, м/с2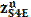 ,а с его конца отрезок
,а с его конца отрезок 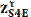 .На конце последнего отрезка будет находится точка s4. Отрезок os4 будет соответствовать вектору ускорения
.На конце последнего отрезка будет находится точка s4. Отрезок os4 будет соответствовать вектору ускорения  .Его численное значение будет равно
.Его численное значение будет равно , м/с2
, м/с2

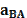
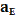
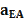




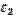
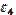

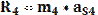 , Н
, Н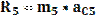 , Н
, Н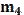 ,
,  – масса звена, кг;
– масса звена, кг;  ,
,  – ускорение его центра масс, м/с2.
– ускорение его центра масс, м/с2. – момент инерции звена, кг*м2;
– момент инерции звена, кг*м2; 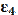 – угловое ускорение звена, 1/c2.
– угловое ускорение звена, 1/c2.
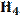 откладывается от
откладывается от 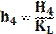 , мм
, мм
 показывает, что направление
показывает, что направление 
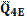 . Для этого из произвольной
. Для этого из произвольной , мм
, мм , мм
, мм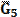
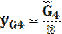 , мм
, мм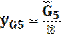 , мм
, мм прибавим вектор
прибавим вектор 
 , мм
, мм и
и  получим вектор
получим вектор 
 , Н
, Н
 , Н
, Н , Н
, Н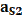 и отстоит от него на расстоянии
и отстоит от него на расстоянии


 показывает, что направление
показывает, что направление 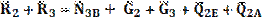
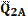 . Для этого из произвольной точки "о" отложим в масштабе силы K, H/мм,
. Для этого из произвольной точки "о" отложим в масштабе силы K, H/мм,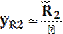 , мм
, мм , мм
, мм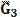
 , мм
, мм , мм
, мм прибавим вектор
прибавим вектор 
 , мм
, мм
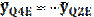
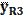 и
и  получим вектор
получим вектор 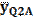
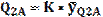 , Н
, Н