
|
|
III. Построение доверительного интервала для математического ожидания генеральной совокупности при неизвестной дисперсии
Для потребителя показатели качества производственного процесса, как правило, не известны, но их можно установить по результатам выборочных статистических испытаний.Следовательно, доверительный интервал, содержащий математическое значение генеральной совокупности, необходимо строить, используя лишь выборочные статистики В начале 20-го века Уильям С. Госсет (William S. Gosset), сотрудник ирландского отделения пивоваренной компании Guinness, заинтересовался проблемой оценки математического ожидания при неизвестном стандартном отклонении. Поскольку компания Guinness запрещала своим сотрудникам публиковать работы под собственными именами, Госсет взял псевдоним Стьюдент. По этой причине распределение, предложенное Госсетом, называется t-распределением Стьюдента (Student's t - distribution). Если случайная величина Xявляется нормально распределенной, то следующая статистика имеет t-распределение с n-1 степенями свободы:
Обратите внимание на то, что это выражение почти совпадает с формулой Z-статистики, только вместо величины s в нем стоит выборочное стандартное отклонение S. Понятие степени свободы поясняется далее. Внешне распределение Стьюдента очень напоминает стандартизованное нормальное распределение. Оба распределения имеют колоколообразную форму и являются симметричными. Однако хвосты t-распределения «тяжелее» (т.е. ограничивают большую площадь), а площадь фигуры в ее центре меньше, чем у стандартизованного нормального распределения. Это происходит потому, что стандартное отклонение s не известно, а вместо него используется его выборочная оценка S. Неопределенность значения s порождает большую изменчивость переменной tпо сравнению с величиной Z. Однако при увеличении количества степеней свободы t-распределение становится все ближе к стандартизованному нормальному распределению. Это происходит потому, что при увеличении объема выборки оценка S становится все точнее. При объеме выборки, равном 120 и более, величина S довольно точно аппроксимирует стандартное отклонение s, так что разница между t-распределением и стандартизованным нормальным отклонением становится минимальной. По этой причине, если объем выборки превышает 120, можно вместо величины tиспользовать переменную Z. Проверка предположений Напомним, что t-распределение основано на предположении, что изучаемая случайная величина Xявляется нормально распределенной. Однако на практике t-распределение можно применять для оценки неизвестного математического ожидания генеральной совокупности при неизвестном стандартном отклонении при достаточно большом объеме выборки и не слишком асимметричном распределении. При работе с небольшими выборками эти условия уже не выполняются автоматически, поэтому их следует проверять. Для этого необходимо строить гистограмму, блочную диаграмму или график нормального распределения. Критические значения для t-распределения с соответствующими степенями свободы табулированы (см. табл. 2). В верхней части таблицы указаны уровни значимости αдля двусторонней критической области, когда α содержит левый и правый «хвосты»t-распределения (см. рис. 1). А в нижней части таблицы указаны уровни значимости αдля односторонней критической области, когда α содержит либо левый, либо правый «хвосты»t-распределения, каждый из которых по площади равен величине α/2. Например, в табл. 2 показано, как найти площадь фигуры, ограниченной t-распределением, имеющим 99 степеней свободы, и соответствующим значением переменной t, если необходимо построить интервал, доверительный уровень которого равен 95%. Этот доверительный уровень ограничен с двух сторон «хвостами» α, в сумме равными величине 0,05.Найдем пересечение столбца, соответствующего величине 0,05, и строки, соответствующей 99 степеням свободы. В этой ячейке записано критическое значение, равное 1,98. Степени свободы Напомним, что для вычисления выборочной дисперсии S2 необходимо определить величину
т.е. при вычислении выборочной дисперсии вначале надо установить значение
Допустим, например, что выборка состоит из 5 чисел, а ее выборочное среднее равно 20. Сколько разных значений необходимо знать для того, чтобы однозначно определить остальные? Если п= 5 и
поскольку
Таким образом, если известны четыре величины, пятое значение уже несвободно, поскольку сумма должна быть равна 100. Например, если нам известны величины 18, 24,19 и 16, пятая величина должна быть равной 23, поскольку сумма равна 100. Доверительный интервал Рассмотрим формулу для вычисления интервала, содержащего математическое ожидание при неизвестном стандартном отклонении с вероятностью (1-α)×100%.
или (7)
где tn-1 - критическое значение t-распределения с n-1 степенями свободы и соответствующим значением α. Чтобы проиллюстрировать применение этой формулы, проведем анализ работы магазина по продаже молочной продукцию. С целью установления математического ожидания стоимости одной покупки извлечена выборка, состоящая из 100 чеков на проданную продукцию в течение последнего месяца. Допустим, что выборочное среднее равно 110,27руб., а выборочное стандартное отклонение — 28,95 руб. Если построить интервал, имеющий доверительный уровень, равный 95%, критическое значение t-распределения равно 1,98 (см. табл. 2). Используя формулу (7), получаем:
104,53 ≤ µ ≤ 116,01.
Таким образом, вероятность того, что средняя стоимость одной покупки находится в интервале от 104,53 до 116,01, равна 95%. Это значит, что если мы извлечем все возможные выборки, состоящие из 100 чеков продажи (что практически невозможно), то 95% доверительных интервалов будут содержать математическое ожидание генеральной совокупности. Корректность этих доверительных интервалов зависит от того, насколько распределение генеральной совокупности близко к нормальному. Поскольку объем выборки довольно велик (n = 100),предположение о нормальном распределении вполне правдоподобно, а полученная оценка математического ожидания довольно надежна. Таким образом, применение t-распределения вполне оправданно. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
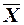 и S.В этом случае в расчетах используется распределение Стьюдента (t-статистика).
и S.В этом случае в расчетах используется распределение Стьюдента (t-статистика). . (6)
. (6)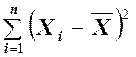 ,
,
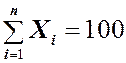 ,
,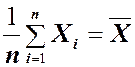 .
.
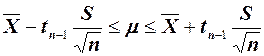 .
. ,
,