
|
|
Тема 15. Дифференциальные уравненияПонятие о дифференциальных уравнениях. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса. Дифференциальные уравнения первого порядка (неполные, с разделяющимися переменными, однородные и линейные) ([1или 6, §12.1, 12.2, 12.4 – 12.6]; [2 или 7, §12.1 – 12.4], или [3, §12.1, 12.2, 12.4 – 12.6, 12.11 – 12.14], или [5, §8.1, 8.2, 8.4 – 8.6, 8.12 – 8.15]). 1. Во многих задачах экономики, физики, экологии встречаются уравнения, связывающие искомую функцию одной или нескольких переменных с производными (или дифференциалами) различных порядков и получившие название дифференциальных уравнений. Одна из таких задач о построении простейшей математической модели демографического процесса ([1или 6, или 3, пример 12.3]) рассматривается в данной теме. 2. Обратите внимание на то, что задача Коши – задача отыскания частного решения дифференциального уравнения первого порядка 3. Студент должен знать основные понятия и уметь решать дифференциальные уравнения первого порядка различных типов – неполные, с разделяющимися переменными, однородные и линейные. Раздел VI. РЯДЫ
Тема 16. Числовые ряды Понятие числового ряда. Сходимость ряда и его сумма. Свойства сходящихся рядов. Необходимый признак сходимости (доказать). Расходимость гармонического ряда. Достаточные признаки сходимости знакоположительных рядов: признак сравнения, Даламбера. Знакопеременные ряды. Признак Лейбница сходимости знакочередующихся рядов. Абсолютная и условная сходимость. ([1 или 6, § 13.1–13.5]; [2 или 7, § 13.1 – 13.3], или [3, §13.1 – 13.7], или [5, §9.1 – 9.7]. При изучении данной темы студенты знакомятся с новой формой изучения числовой последовательности. Следует уяснить, что обозначение Нужно уяснить, что необходимый признак сходимости (для сходящихся рядов Применяя признаки сравнения, можно использовать в качестве «эталонных» следующие ряды: 1) геометрический ряд 2) гармонический ряд 3) обобщенный гармонический ряд К признаку сравнения обращаются тогда, когда признак Даламбера показывает, что Говоря о сходимости знакочередующихся рядов, следует иметь в виду два типа сходимости: абсолютную и условную. Важность этих понятий связана с тем, что абсолютно сходящиеся ряды обладают некоторыми свойствами конечных сумм в отличие от условно сходящихся рядов. Решать вопрос о сходимости знакочередующегося ряда рекомендуем в таком порядке. 1. Составить ряд из абсолютных величин членов данного знакочередующегося ряда. 2. Исследовать сходимость полученного ряда. Может оказаться, что этот ряд сходится. Тогда исходный ряд также сходится, и притом абсолютно. Задача решена. Если же составленный ряд расходится, то в этом случае о сходимости или расходимости исходного ряда сделать вывод нельзя; необходимо выполнить пункт 3. 3. Исследовать условную сходимость исходного знакочередующегося ряда, например, по признаку Лейбница.
Вопросы для самопроверки 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  всегда имеет решение и притом единственное. Геометрически это означает существование единственной интегральной кривой дифференциального уравнения, проходящей через каждую точку открытого множества, в которой функция
всегда имеет решение и притом единственное. Геометрически это означает существование единственной интегральной кривой дифференциального уравнения, проходящей через каждую точку открытого множества, в которой функция  определена.
определена. , или u1 + u2 + …+ un + …, – символ, который не следует смешивать с обычной (конечной) суммой. Сумма и сходимость ряда определяется через предельный переход. При рассмотрении ряда могут решаться задачи: определение его суммы и исследование сходимости. Решение первой задачи «перекрывает» и вторую, но это не всегда возможно или вызывает значительные трудности. Решение второй задачи не менее важно, так как в случае, если ряд сходится, его сумма существует и ее можно найти приближенно с любой степенью точности, взяв сумму достаточного числа его первых членов.
, или u1 + u2 + …+ un + …, – символ, который не следует смешивать с обычной (конечной) суммой. Сумма и сходимость ряда определяется через предельный переход. При рассмотрении ряда могут решаться задачи: определение его суммы и исследование сходимости. Решение первой задачи «перекрывает» и вторую, но это не всегда возможно или вызывает значительные трудности. Решение второй задачи не менее важно, так как в случае, если ряд сходится, его сумма существует и ее можно найти приближенно с любой степенью точности, взяв сумму достаточного числа его первых членов. при
при 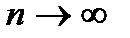 ) не является достаточным, но из необходимого признака сходимости следует, что если предел общего члена
) не является достаточным, но из необходимого признака сходимости следует, что если предел общего члена  , то ряд расходится. Поэтому исследование сходимости числового ряда рекомендуется начинать с вычисления предела его общего члена (если он находится не очень сложно). Если предел окажется равным нулю, то это означает, что ряд может сходиться. Чтобы установить, сходится ли ряд, далее применяют достаточные признаки сходимости.
, то ряд расходится. Поэтому исследование сходимости числового ряда рекомендуется начинать с вычисления предела его общего члена (если он находится не очень сложно). Если предел окажется равным нулю, то это означает, что ряд может сходиться. Чтобы установить, сходится ли ряд, далее применяют достаточные признаки сходимости. – сходится при |q|<1, расходится при
– сходится при |q|<1, расходится при 
 – расходится;
– расходится;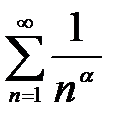 – сходится при
– сходится при  расходится при
расходится при 
 . Во всех этих случаях применения достаточных признаков сходимости речь идет об исследовании рядов с положительными членами.
. Во всех этих случаях применения достаточных признаков сходимости речь идет об исследовании рядов с положительными членами.