III Вычислительные методы
Ответы
II
Исследование задач на безусловный минимум (с док.) Схема исследования.
ГЛАВА III НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Здесь рассматривается задача  , (1) , (1)
в которой функция 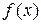 в общем случае является ни линейной, ни выпуклой, а при формировании множества в общем случае является ни линейной, ни выпуклой, а при формировании множества 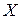 могут участвовать нелинейные ограничения. Справедливо включение ЛП могут участвовать нелинейные ограничения. Справедливо включение ЛП 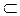 ВП ВП 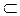 НЛП. НЛП.
Классификация
Задача (1) имеет общую форму, и если не накладывать дополнительные условия на функцию 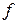 и множество и множество  , то содержательных результатов не удается получить. Поэтому задачу (1) разбивают на специальные классы задач, используя аналитическое свойство функции (гладкость) и форму ограничений (уравнений и неравенств). , то содержательных результатов не удается получить. Поэтому задачу (1) разбивают на специальные классы задач, используя аналитическое свойство функции (гладкость) и форму ограничений (уравнений и неравенств).
I. Задача на безусловный минимум

На множество планов не накладывается никаких ограничений, отсюда и название класса. Предполагается  или или  . .
Задача имеет вид:  (1) (1)
то есть 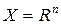 . .
Условие оптимальности
Теорема 1.Если 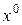 – локально-оптимальный план, то – локально-оптимальный план, то 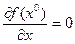 (2) (2)
Теорема 2 (Необходимое условие оптимальности второго порядка). Если 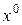 – локально-оптимальный план, то – локально-оптимальный план, то 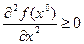 (3) (3)
Определение.Точка  называется стационарной точкой функции называется стационарной точкой функции 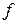 , если она является решением системы , если она является решением системы  (4) (4)
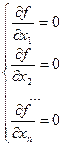 (4) (4)
Теорема 3 (Достаточное условие оптимальности). Если 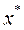 – стационарная точка функции – стационарная точка функции 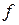 и и 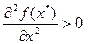 , (5)то , (5)то  – локально-оптимальный план (1) (по крайней мере). – локально-оптимальный план (1) (по крайней мере).
Доказательство. Доказательство теорем 1-3 основано на разложении функции 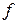 ( (  переменных) в ряд в окрестности точки (см. главу 2). переменных) в ряд в окрестности точки (см. главу 2).
Ч.т.д.
Замечание.При проверке условий (3) и (5) применяются критерии Сильвестра неотрицательности и положительности квадратных матриц.
Схема исследования задач типа (1)
1) Проверяем условие существования решения задачи (1), при этом применяется критерий существования решения  . В общем случае, при . В общем случае, при  , вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня. , вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.
2) Составляем систему (4) и находим стационарные точки функции 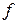 (все). Только среди них может находиться оптимальный план и все локально-оптимальные планы. Пусть (все). Только среди них может находиться оптимальный план и все локально-оптимальные планы. Пусть 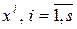 – все стационарные точки функции – все стационарные точки функции 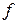 . .
3) Для каждой стационарной точки проверяем выполнение или невыполнение условий (3)-(5). Пусть  – стационарная точка, тогда возможны случаи: – стационарная точка, тогда возможны случаи:
а) 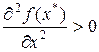 . Тогда, согласно теореме 3 . Тогда, согласно теореме 3  – локально-оптимальный план. – локально-оптимальный план.
б) 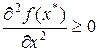 . Тогда для нее выполняются условия теоремы 2, но не выполняются условия теоремы 3. Тем не менее, она остается подозрительной на решение задачи (1) (то есть она может оказаться и оптимальным планом и локально-оптимальным планом). . Тогда для нее выполняются условия теоремы 2, но не выполняются условия теоремы 3. Тем не менее, она остается подозрительной на решение задачи (1) (то есть она может оказаться и оптимальным планом и локально-оптимальным планом).
в) Не выполняется ни а) ни б). Тогда эту точку исключают из дальнейшего рассмотрения.
4)Делаем окончательный вывод: среди точек, оказавшихся либо локально-оптимальными планами, либо подозрительных на решение, находим лучшую, то есть подставляем точки в целевую функцию и лучшей будет точка с наименьшим значением функции. Если доказано существование решения и построены все стационарные точки, то лучшая точка будет оптимальным планом. В общем случае, из-за сложности функции 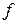 и невозможности найти все решения системы (4) исследование нельзя провести полностью и лучшая точка остается подозрительной на решение задачи. и невозможности найти все решения системы (4) исследование нельзя провести полностью и лучшая точка остается подозрительной на решение задачи.
2. Принцип Лагранжа + схема лаб.раб.№2 (часть 2)
Пусть дана задача: 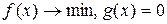 (1) (1)
Теорема 1(Обобщённое правило множителей Лагранжа). Если 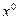 – локально-оптимальный план задачи (1), то необходимо найдётся такой обобщённый вектор Лагранжа – локально-оптимальный план задачи (1), то необходимо найдётся такой обобщённый вектор Лагранжа  , что , что

Определение.Некоторый план задачи (1) 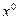 (здесь необязательно оптимальный) будем называть обыкновенным, если вектора (здесь необязательно оптимальный) будем называть обыкновенным, если вектора
 (7) (7)
линейно независимы 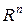 . .
Теорема 2 (Классическое правило множителей Лагранжа).Если 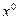 – обыкновенный локально-оптимальный план задачи (1), то всегда найдётся такой единственный классический вектор Лагранжа – обыкновенный локально-оптимальный план задачи (1), то всегда найдётся такой единственный классический вектор Лагранжа 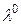 , что выполняется условие: , что выполняется условие:
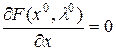




III Вычислительные методы
1. Метод ветвей и границ (общая схема)+лаб.раб.№3 (часть 2)
Метод ветвей и границ является одним из самых популярных методов перебора, который позволяет значительно сокращать объём перебираемых планов за счёт исключения бесперспективных подмножеств планов, то есть таких, которые заведомо не содержат решения.
Метод применяют к задачам:
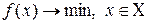 , (1) , (1)
для которых выполняются два предположения:
1. множество планов  и любое его подмножество и любое его подмножество 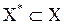 можно дробить (ветвить) на более мелкие, (причём дробление должно быть таким, чтобы во-первых, попарное пересечение более мелких подмножеств было пустым, а во-вторых, в объединении они должны давать дробимые подмножества). можно дробить (ветвить) на более мелкие, (причём дробление должно быть таким, чтобы во-первых, попарное пересечение более мелких подмножеств было пустым, а во-вторых, в объединении они должны давать дробимые подмножества).
2. для множества  и для любого его подмножества и для любого его подмножества 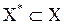 может быть вычислена эффективная нижняя грань значений целевой функций на нём, то есть для может быть вычислена эффективная нижняя грань значений целевой функций на нём, то есть для 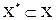 можно построить число можно построить число 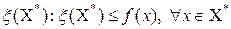 (5) (5)
Общая схема
В методе на каждой итерации строится список  из перспективных подмножеств, одно из которых, по крайне мере содержит оптимальный план. На нулевой итерации из перспективных подмножеств, одно из которых, по крайне мере содержит оптимальный план. На нулевой итерации 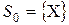 . Вычисляем оценку итерации . Вычисляем оценку итерации 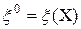 , рекорд итерации , рекорд итерации 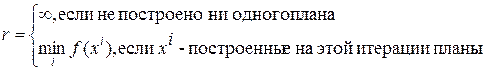 . .
Вычисляем разность 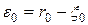 . Возможны случаи: . Возможны случаи:
1. 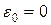 . В этом случае рекордный план будет оптимальным планом задачи, так как на нём достигалась нижняя граница. . В этом случае рекордный план будет оптимальным планом задачи, так как на нём достигалась нижняя граница.
2. 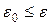 , где , где  - малое положительное число, заданная точность вычисления. В этом случае рекордный план можно взять в качестве - малое положительное число, заданная точность вычисления. В этом случае рекордный план можно взять в качестве  - оптимального, то есть приближённого решения задачи (1). - оптимального, то есть приближённого решения задачи (1).
3. 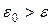 . Тогда заданная точность не достигнута. Переходим к первой итерации. Для этого в соответствие с первым предположением . Тогда заданная точность не достигнута. Переходим к первой итерации. Для этого в соответствие с первым предположением  ветвим на более мелкие. Для каждого вычисляем границу по второму предположению, и бесперспективные подмножества отбрасываем, а перспективные включаем в список для первой итерации. ветвим на более мелкие. Для каждого вычисляем границу по второму предположению, и бесперспективные подмножества отбрасываем, а перспективные включаем в список для первой итерации.
Определение. Пусть на некоторой итерации есть подмножество  и вычислен рекорд и вычислен рекорд 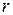 . Тогда множество будет перспективным, если . Тогда множество будет перспективным, если 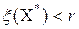 . Если . Если 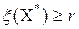 , то, очевидно, на нём нет планов, лучших, чем рекордный и, ветвь можно отсечь, это подмножество будет бесперспективным. , то, очевидно, на нём нет планов, лучших, чем рекордный и, ветвь можно отсечь, это подмножество будет бесперспективным.
Пусть 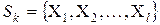 – список перспективных подмножеств – список перспективных подмножеств 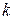 -ой итерации. Вычисляем оценку итерации -ой итерации. Вычисляем оценку итерации 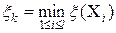 . Вычисляем рекорд итерации . Вычисляем рекорд итерации  . .
Вычисляем разность 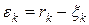 . .
Совершаем анализ:
1. если 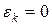 , то построен оптимальный план. Записываем ответ. , то построен оптимальный план. Записываем ответ.
2. если 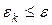 , то построен , то построен  -оптимальный план. Записываем ответ. -оптимальный план. Записываем ответ.
3. если 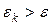 , то переходим к , то переходим к  ой итерации. Для этого выбираем из ой итерации. Для этого выбираем из  наиболее перспективное подмножество ( с наименьшей нижней границей) и дробим его по первому предположению. В наиболее перспективное подмножество ( с наименьшей нижней границей) и дробим его по первому предположению. В 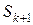 включаем перспективные подмножества из вновь полученных дроблением и остальных подмножеств множества включаем перспективные подмножества из вновь полученных дроблением и остальных подмножеств множества 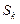 . .
И так далее.
Ясно, что на итерациях 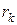 уменьшаются, а уменьшаются, а  увеличиваются (чем мельче подмножество, тем точнее можно для неё построить границу). Следовательно, числа увеличиваются (чем мельче подмножество, тем точнее можно для неё построить границу). Следовательно, числа  будут уменьшаться и, в конце концов, метод ветвей и границ позволит, решить задачу (1). будут уменьшаться и, в конце концов, метод ветвей и границ позволит, решить задачу (1).
2. Методы безусловной минимизации(градиент, наискорейшего спуска, Ньютон,…) +лаб.раб.№4 (часть 2)
Будем рассматривать задачу:
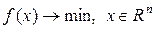 (1)Пусть задано начальное приближение (1)Пусть задано начальное приближение  . Основная идея, которая используется при разработке методов оптимизации – идея аппроксимации элементов задачи некоторыми более простыми элементами, в результате получается другая задача, которая является, как правило, задачей линейного программирования и решение этой задачи принимается за приближённое решение задачи (1). . Основная идея, которая используется при разработке методов оптимизации – идея аппроксимации элементов задачи некоторыми более простыми элементами, в результате получается другая задача, которая является, как правило, задачей линейного программирования и решение этой задачи принимается за приближённое решение задачи (1).
Аппроксимация функций
Определение. Аппроксимацией 1-го порядка или линейной аппроксимацией функции 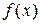 класса класса  в окрестности некоторой точки в окрестности некоторой точки 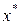 называют линейную функцию называют линейную функцию
 (2) (2)
Для 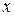 в малой окрестности в малой окрестности 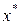 величина величина 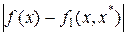 ~ ~  . .
Определение.Аппроксимацией 2-го порядка или квадратной аппроксимацией функции 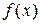 класса класса  в окрестности некоторой точки в окрестности некоторой точки 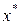 называют функцию называют функцию
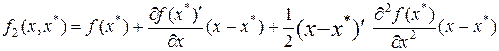 (3)функция (3)функция  будет квадратичной функцией по будет квадратичной функцией по 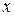 и справедлива оценка и справедлива оценка  ~ ~ 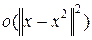 . .
Эти аппроксимации основаны на разложении в ряд Тейлора функции 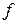 . В оптимизации могут использоваться и другие виды аппроксимаций: если . В оптимизации могут использоваться и другие виды аппроксимаций: если 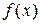 – периодическая функция или близка к ней, то её можно аппроксимировать кусками рядов Фурье. – периодическая функция или близка к ней, то её можно аппроксимировать кусками рядов Фурье.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , (1)
, (1)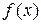 в общем случае является ни линейной, ни выпуклой, а при формировании множества
в общем случае является ни линейной, ни выпуклой, а при формировании множества 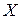 могут участвовать нелинейные ограничения. Справедливо включение ЛП
могут участвовать нелинейные ограничения. Справедливо включение ЛП 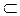 ВП
ВП 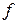 и множество
и множество  , то содержательных результатов не удается получить. Поэтому задачу (1) разбивают на специальные классы задач, используя аналитическое свойство функции (гладкость) и форму ограничений (уравнений и неравенств).
, то содержательных результатов не удается получить. Поэтому задачу (1) разбивают на специальные классы задач, используя аналитическое свойство функции (гладкость) и форму ограничений (уравнений и неравенств).
 или
или  .
.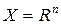 .
.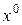 – локально-оптимальный план, то
– локально-оптимальный план, то 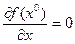 (2)
(2)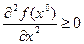 (3)
(3) называется стационарной точкой функции
называется стационарной точкой функции 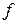 , если она является решением системы
, если она является решением системы  (4)
(4)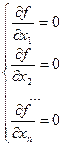 (4)
(4)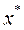 – стационарная точка функции
– стационарная точка функции 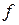 и
и 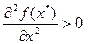 , (5)то
, (5)то  переменных) в ряд в окрестности точки (см. главу 2).
переменных) в ряд в окрестности точки (см. главу 2). . В общем случае, при
. В общем случае, при  , вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.
, вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.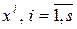 – все стационарные точки функции
– все стационарные точки функции 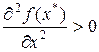 . Тогда, согласно теореме 3
. Тогда, согласно теореме 3 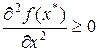 . Тогда для нее выполняются условия теоремы 2, но не выполняются условия теоремы 3. Тем не менее, она остается подозрительной на решение задачи (1) (то есть она может оказаться и оптимальным планом и локально-оптимальным планом).
. Тогда для нее выполняются условия теоремы 2, но не выполняются условия теоремы 3. Тем не менее, она остается подозрительной на решение задачи (1) (то есть она может оказаться и оптимальным планом и локально-оптимальным планом).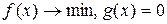 (1)
(1)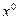 – локально-оптимальный план задачи (1), то необходимо найдётся такой обобщённый вектор Лагранжа
– локально-оптимальный план задачи (1), то необходимо найдётся такой обобщённый вектор Лагранжа  , что
, что
 (7)
(7)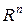 .
.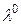 , что выполняется условие:
, что выполняется условие: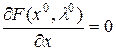




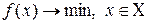 , (1)
, (1) и любое его подмножество
и любое его подмножество 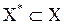 можно дробить (ветвить) на более мелкие, (причём дробление должно быть таким, чтобы во-первых, попарное пересечение более мелких подмножеств было пустым, а во-вторых, в объединении они должны давать дробимые подмножества).
можно дробить (ветвить) на более мелкие, (причём дробление должно быть таким, чтобы во-первых, попарное пересечение более мелких подмножеств было пустым, а во-вторых, в объединении они должны давать дробимые подмножества). и для любого его подмножества
и для любого его подмножества 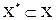 можно построить число
можно построить число 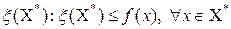 (5)
(5) из перспективных подмножеств, одно из которых, по крайне мере содержит оптимальный план. На нулевой итерации
из перспективных подмножеств, одно из которых, по крайне мере содержит оптимальный план. На нулевой итерации 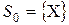 . Вычисляем оценку итерации
. Вычисляем оценку итерации 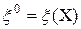 , рекорд итерации
, рекорд итерации 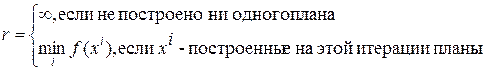 .
.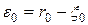 . Возможны случаи:
. Возможны случаи: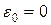 . В этом случае рекордный план будет оптимальным планом задачи, так как на нём достигалась нижняя граница.
. В этом случае рекордный план будет оптимальным планом задачи, так как на нём достигалась нижняя граница.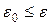 , где
, где  - малое положительное число, заданная точность вычисления. В этом случае рекордный план можно взять в качестве
- малое положительное число, заданная точность вычисления. В этом случае рекордный план можно взять в качестве 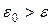 . Тогда заданная точность не достигнута. Переходим к первой итерации. Для этого в соответствие с первым предположением
. Тогда заданная точность не достигнута. Переходим к первой итерации. Для этого в соответствие с первым предположением  и вычислен рекорд
и вычислен рекорд 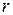 . Тогда множество будет перспективным, если
. Тогда множество будет перспективным, если 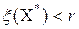 . Если
. Если 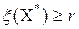 , то, очевидно, на нём нет планов, лучших, чем рекордный и, ветвь можно отсечь, это подмножество будет бесперспективным.
, то, очевидно, на нём нет планов, лучших, чем рекордный и, ветвь можно отсечь, это подмножество будет бесперспективным.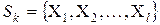 – список перспективных подмножеств
– список перспективных подмножеств 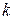 -ой итерации. Вычисляем оценку итерации
-ой итерации. Вычисляем оценку итерации 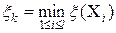 . Вычисляем рекорд итерации
. Вычисляем рекорд итерации  .
.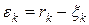 .
.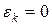 , то построен оптимальный план. Записываем ответ.
, то построен оптимальный план. Записываем ответ.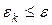 , то построен
, то построен 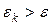 , то переходим к
, то переходим к  ой итерации. Для этого выбираем из
ой итерации. Для этого выбираем из 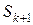 включаем перспективные подмножества из вновь полученных дроблением и остальных подмножеств множества
включаем перспективные подмножества из вновь полученных дроблением и остальных подмножеств множества 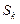 .
.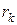 уменьшаются, а
уменьшаются, а  увеличиваются (чем мельче подмножество, тем точнее можно для неё построить границу). Следовательно, числа
увеличиваются (чем мельче подмножество, тем точнее можно для неё построить границу). Следовательно, числа  будут уменьшаться и, в конце концов, метод ветвей и границ позволит, решить задачу (1).
будут уменьшаться и, в конце концов, метод ветвей и границ позволит, решить задачу (1).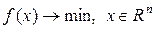 (1)Пусть задано начальное приближение
(1)Пусть задано начальное приближение  . Основная идея, которая используется при разработке методов оптимизации – идея аппроксимации элементов задачи некоторыми более простыми элементами, в результате получается другая задача, которая является, как правило, задачей линейного программирования и решение этой задачи принимается за приближённое решение задачи (1).
. Основная идея, которая используется при разработке методов оптимизации – идея аппроксимации элементов задачи некоторыми более простыми элементами, в результате получается другая задача, которая является, как правило, задачей линейного программирования и решение этой задачи принимается за приближённое решение задачи (1).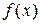 класса
класса  в окрестности некоторой точки
в окрестности некоторой точки 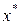 называют линейную функцию
называют линейную функцию (2)
(2)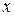 в малой окрестности
в малой окрестности 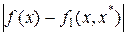 ~
~  .
.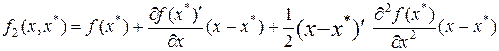 (3)функция
(3)функция  будет квадратичной функцией по
будет квадратичной функцией по  ~
~ 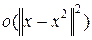 .
.