
|
|
Определение устойчивости по логарифмическим частотным характеристикам12 Для определения устойчивости по критерию Найквиста можно строить не АФХ, а ЛАЧХ & ЛФЧХ разомкнутой системы.
Чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы сдвиг фазы на частоте единичного усиления разомкнутой системы W(jω) не достигал значения −180°.
Если система условно устойчивая, то при модулях больших единицы, фазовый сдвиг может достигать значения −180° четное число раз.
Критерий Найквиста - частотный критерий, позволяющий по виду амплитудно-фазовой частотной характеристики разомкнутой системы оценить устойчивость работы замкнутой системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами. Критерий Найквиста формулируется по разному в зависимости от того, устойчива разомкнутая система или нет.
АФЧХ астатической системы, начинаясь на вещественной положительной полуоси, при ω->0 дугой бесконечно большого радиуса перемещается на угол, равный -ν
Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до
Уравнение статического режима представляют в виде:
Здесь
П-регулятор
коэффициента передачи регулятора П-регулятор представляет собой одно из самых простых и распространенных устройств и алгоритмов управления. П-регулятор – это устройство в обратной связи, которое формирует управляющий сигнал. П-регулятор выдает выходной сигнал, пропорциональный входному, с коэффициентом пропорциональности К. Выходной сигнал, вырабатываемый пропорциональной частью П-регулятора , противодействует отклонению регулируемой величины от данного значения, которое наблюдается в данный момент. Выход П-регулятор выдаст тем больше, чем больше отклонение. Если П-регулятор имеет входной сигнал, который равняется заданному значению, то выходной равен 0. П-регулятор имеет существенный недостаток в том, что при его использовании значение регулируемой величины никогда не стабилизируется на заданном значении. Все из-за так называемой статической ошибки. Она равна отклонению регулируемой величины, которая дает такой выходной сигнал, который стабилизирует выходную величину именно на данном значении. Это важно учитывать при выборе закона регулирования.
Пропорционально-интегрально-дифференциальный (ПИД) регулятор — наиболее эффективный и распространенный вид регулятора, обеспечивающий достаточно высокую точность при управлении различными процессами. ПИД-регулятор вырабатывает выходной сигнал, который рассчитывается по следующей формуле:
Как видно из формулы, сигнал управления является суммой трех составляющих: · пропорциональной (1-е слагаемое); · интегральной (3-е слагаемое); · дифференциальной (2-е слагаемое). Пропорциональная составляющая зависит от рассогласования Ei и отвечает за реакцию на мгновенную ошибку регулирования. Интегральная составляющая содержит в себе накопленную ошибку регулирования, которая является дополнительным источником выходной мощности и позволяет добиться максимальной скорости достижения уставки при отсутствии перерегулирования. Дифференциальная составляющая зависит от скорости изменения параметра / , вызывающей реакцию регулятора на резкое изменение измеряемого параметра, возникшее, например, в результате внешнего возмущающего воздействия. Для эффективной работы ПИД-регулятора необходимо подобрать для конкретного объекта регулирования значения коэффициентов ПИД-регулятора Xp, и . Это можно cделать вручную или воспользоваться автонастройкой.
Частные случаи ПИД-регулирования, поясняющие действие его составляющих: · пропорциональное регулирование (П-закон, аналоговый П-регулятор) · пропорционально-дифференциальное регулирование (ПД-закон) · пропорционально-интегральное регулирование (ПИ-закон) ПИД-регуляторы (ПИД – пропорционально – интегродифференциальный) получили самое широкое распространение при управлении производственными и технологическими процессами. Основное уравнение ПИД-регулятора имеет следующий вид:
где kp, ki, kd – константы, выбираемые в процессе проектирования. С их помощью удается обеспечить соизмеримость отдельных слагаемых формулы (1). Дифференциальная составляющая в формуле (1) позволяет повысить быстродействие регулятора, предсказывая будущее поведение процесса. Интегральная составляющая в формуле (1) призвана ликвидировать статические ошибки управления, поскольку интеграл даже от малой ошибки может быть значительной величиной, вызывающей реакцию регулятора. Хотя ПИД-регулятор представляет собой систему второго порядка, его можно успешно применять для управления процессами, имеющими более высокий порядок. Это вызвано возможностью аппроксимации многих систем высокого порядка системами второго порядка. На практике часто используются упрощенные версии ПИД-регулятора – П-, И-, ПД- и ПИ-регуляторы, описываемые соответственно формулами:
При большом значении коэффициента усиления П- и И- регуляторы ведут себя как двухпозиционное реле. Существует инженерный подход к синтезу ПИД-регуляторов – методика Зиглера-Николса [Олссон Г., Пьяни Дж. Цифровые системы автоматизации и управления. СПб., 2001.], которая предполагает следующие шаги: 1. Коэффициенты kd и ki устанавливаются равными нулю, а коэффициент kp увеличивается до тех пор, пока система не потеряет устойчивость. 2. Предельное значение kp обозначается как ku, а период автоколебаний как pu. 3. Значения коэффициентов ПИД-регулятора рассчитываются по следующим формулам: kp = 0,6ku; ki = 1,2(ku/pu); kd = 3kupu /40. В аналоговых промышленных ПИД-регуляторах коэффициенты настраиваются вручную. Следует заметить, что коэффициент K, от которого строится корневой годограф, соответствует, по сути, П-регулятору. Процесс построения корневого годографа нескорректированной системы можно рассматривать как одновременный синтез этой системы с использованием П-регулятора [4].
Корневым годографом (КГ) называется совокупность траекторий перемещения всех корней характеристического уравнения замкну) той системы при изменении какого-либо параметра этой системы. Обычно метод КГ позволяет находить полюса и нули ПФ замкну) той системы, располагая полюсами и нулями разомкнутой системы при изменении коэффициента усиления разомкнутой системы K. Логарифмическая амплитудно-фазовая частотная характеристика (ЛАФЧХ, в иностранной литературе часто называют диаграммой Боде) — представление частотного отклика линейной стационарной системы в логарифмическом масштабе. ЛАФЧХ строится в виде двух графиков: логарифмической амплитудно-частотной характеристики и логарифмической фазо-частотной характеристики, которые обычно располагают друг под другом. ЛАЧХ[править | править вики-текст] ЛАЧХ — это зависимость модуля коэффициента усиления (напряжения, тока или мощности) устройства, ( Масштаб по оси абсцисс ЛАЧХ[править | править вики-текст] По оси абсцисс откладывается частота в логарифмическом масштабе, единица измерения — безразмерная величина: · декада (дек): 1 декада равна изменению частоты в 10 раз. · октава(окт): 1 октава равна изменению частоты в 2 раза. Масштаб по оси ординат ЛАЧХ[править | править вики-текст] По оси ординат откладывается амплитуда выходного сигнала в логарифмических безразмерных величинах: · децибел (дБ) (десятая часть бела) — это отношение мощностей (10 децибел равно изменению мощности в 10 раз). 1 децибел равен (для амплитуд размерности напряжения) одной двадцатой изменению амплитуды сигналов в 10 раз. · непер (Нп): 1 непер равен изменению амплитуды сигналов в е раз ЛФЧX[править | править вики-текст] ЛФЧХ — это зависимость фазы выходного сигнала от частоты в полулогарифмическом масштабе · по оси абсцисс откладывается частота в логарифмическом масштабе (в декадах или октавах) · по оси ординат откладывается выходная фаза в угловых градусах или радианах. Неперы и октавы в настоящее время являются устаревшими и практически не используются. Причины построения амплитудных и фазных характеристик в логарифмическом масштабе — возможность исследования характеристик в большом диапазоне. Асимптотические ЛАЧХ и ЛФХЧ[править | править вики-текст] Собственно ЛАЧХ и ЛФЧХ мало используются на практике. Для более наглядного анализа характеристик применяются их модифицированные варианты —асимптотическая логарифмическая аплитудо-частотная характеристика (АЛАЧХ) и асимптотическая логарифмическая фазо-частотная характеристика (АЛФЧХ), при этом кривая заменяется отрезками ломаной прямой. Обычно слово «асимптотическая» опускают, но всегда надо помнить, что АЛАЧХ (АЛФЧХ) и ЛАЧХ (ЛФЧХ) — это разные характеристики. Анализ систем с помощью АЛФЧХ весьма прост и удобен, поэтому находит широкое применение в различных отраслях техники, таких, как цифровая обработка сигналов, электротехника и теория управления. Названия[править | править вики-текст] В западной литературе используется название диаграмма Боде или график Боде, по имени выдающегося инженера Хенрика Боде (англ. Hendrik Wade Bode). В инженерных кругах название обычно сокращается до ЛАХ. В пакете прикладных программ для инженерных вычислений GNU Octave и MATLAB для построения ЛАФЧХ используется функция bode. Использование[править | править вики-текст] Свойства и особенности[править | править вики-текст] Если передаточная функция системы является рациональной, тогда ЛАФЧХ может быть аппроксимирована прямыми линиями. Это удобно при рисовании ЛАФЧХ вручную, а также при составлении ЛАФЧХ простых систем. С помощью ЛАФЧХ удобно проводить синтез систем управления, а также цифровых и аналоговых фильтров: в соответствии с определёнными критериями качества строится желаемая ЛАФЧХ, аппроксимированная с помощью прямых линий, которая затем разбивается на ЛАФЧХ отдельных элементарных звеньев, из которых восстанавливается передаточная функция системы (регулятора) или фильтра. ЛАЧХ[править | править вики-текст] На графике ЛАЧХ абсциссой является частота в логарифмическом масштабе, по оси ординат отложена амплитуда передаточной функции в децибелах. Представление АЧХ в логарифмическом масштабе упрощает построение характеристик сложных систем, так как позволяет заменить операцию перемножения АЧХ звеньев сложением, что вытекает из свойства логарифма: ФЧХ[править | править вики-текст] На графике фазо-частотной характеристики абсциссой является частота в логарифмическом масштабе, по оси ординат отложен фазовый сдвиг выходного сигнала системы относительно входного (обычно в градусах). Также возможен вариант, когда по оси ординат откладывается фазовый сдвиг в логарифмическом масштабе, в этом случае характеристика будет называться ЛФЧХ. Случай минимально-фазовых систем[править | править вики-текст] Амлитуда и фаза системы редко меняются независимо друг от друга — при изменении амплитуды меняется и фаза, и наоборот. Для минимально-фазовых систем ЛФЧХ и ЛАЧХ могут быть однозначно определены друг из друга с помощью преобразования Гильберта — Уорренгтона. Построение ЛАФЧХ[править | править вики-текст] Основная идея основывается на следующем математическом правиле сложения логарифмов. Если передаточную функцию можно представить в виде дробно-рациональной функции
то:
После разбиения передаточной функции на элементарные звенья можно построить ЛАФЧХ каждого отдельного звена, а результирующую ЛАФЧХ получить простым сложением. Построение асимптотической ЛАЧХ (аппроксимация ЛАЧХ прямыми линиями)[править | править вики-текст] При построении ЛАЧХ для оси ординат обычно используется масштаб
где · в каждом · в каждом · Начальное значение графика можно найти простой подстановкой значения круговой частоты · Начальный наклон графика зависит от числа и порядка нулей и полюсов, которые меньше начального значения частоты. Он может быть найден с помощью первых двух правил. · В случае наличия комплексно-сопряжённых нулей или полюсов необходимо использовать звенья второго порядка, Корректировка аппроксимированной ЛАЧХ[править | править вики-текст] Для корректировки ЛАЧХ, аппроксимированную прямыми линиями, надо: · в каждом нуле поставить точку на · в каждом полюсе поставить точку на · плавно соединить точки, используя прямые линии в качестве асимптот Построение асимптотической ЛФЧХ (аппроксимация)[править | править вики-текст] Для построения аппроксимированной ФЧХ используют запись передаточной функции в том же виде, что и для ЛАЧХ:
Основной принцип построения ФЧХ — начертить отдельные графики для каждого полюса или нуля, затем сложив их. Точная кривая фазо-частотной характеристики задаётся уравнением:
Для того, чтобы нарисовать ФЧХ для каждого полюса или нуля, используют следующие правила: · если · если · для нуля сделать наклон линии вверх на · для полюса наклонить линию вниз на · обнулить наклон снова когда фаза изменится на · сложить все линии и нарисовать результирующую. ·
В астатической системе статическая ошибка равна нулю, т.е. система после процесса регулирования возвращается в исходное состояние равновесия. В астатических САУ конечное и исходное равновесие совпадает с заданием. Поэтому в этих САУ динамическая ошибка равна максимальному отклонению параметра в процессе регулирования (рис. 6.17а). В статической системе в установившемся состоянии - через достаточно долгое время после начала регулирования τ, всегда имеется статическая ошибка регулирования (рис.6.17б). Динамическая ошибка - это максимальное в процессе регулирования отклонение регулируемого параметра от конечного состояния равновесия Δдин= (Yвых маx - Yвых ном). Время регулирования - это отрезок времени Δτ с момента нанесения на замкнутую САУ возмущающего воздействия, по истечении которого отличие регулируемого параметра от конечного состояния равновесия становится равным и меньше ± 5% от заданной величины. Если заданная величина равна нулю, то ± 5% берут от величины динамической ошибки. Перерегулирование - это динамическая ошибка, отнесённая к номинальной величине регулируемого параметра в процентах. Перерегулирование вычисляют по формуле: σ = (Yвых маx - Yвых ном)100%/Yвых ном

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 не охватывала точку с координатами -I, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -I, j0, то система будет нейтральной. На рис.4.4 представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.
не охватывала точку с координатами -I, j0. Если АФЧХ разомкнутой системы проходит через точку с координатами -I, j0, то система будет нейтральной. На рис.4.4 представлены АФЧХ разомкнутых статических систем. Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.
 , где ν - порядок астатизма. На рис.4.5 изображена АФЧХ устойчивой в замкнутом состоянии астатической системы первого порядка.
, где ν - порядок астатизма. На рис.4.5 изображена АФЧХ устойчивой в замкнутом состоянии астатической системы первого порядка.
 . Первая строка матрицы Гурвица составляется из коэффициентов уравнения (205), начиная со второго, через один. Вторая строка составляется из коэффициентов уравнения (205), начиная с первого, через один. Элементы каждой последующей строки формируются из коэффициентов, имеющих индекс на единицу ниже индекса элемента в соответствующем столбце вышележащей строки. Матрица Гурвица представлена на рис. 73.
. Первая строка матрицы Гурвица составляется из коэффициентов уравнения (205), начиная со второго, через один. Вторая строка составляется из коэффициентов уравнения (205), начиная с первого, через один. Элементы каждой последующей строки формируются из коэффициентов, имеющих индекс на единицу ниже индекса элемента в соответствующем столбце вышележащей строки. Матрица Гурвица представлена на рис. 73.
 Рис. 73. Матрица Гурвица
Определение. Чтобы линейная система уравнений была устойчива, необходимо и достаточно положительности диагональных миноров матрицы Гурвица при условии
Рис. 73. Матрица Гурвица
Определение. Чтобы линейная система уравнений была устойчива, необходимо и достаточно положительности диагональных миноров матрицы Гурвица при условии  . Можно показать, что для уравнений первого и второго порядков условием устойчивости, по Гурвицу, является положительность их коэффициентов.
Для уравнения третьего порядка
. Можно показать, что для уравнений первого и второго порядков условием устойчивости, по Гурвицу, является положительность их коэффициентов.
Для уравнения третьего порядка
 матрица Гурвица
матрица Гурвица
 .
Условия устойчивости:
.
Условия устойчивости:
 ,
,  , (207)
, (207)
 или
или  , (208)
, (208)
 или
или  . (209)
Из анализа условий (207) … (209) следует, что для устойчивости системы управления, имеющей характеристическое уравнение (205), кроме положительности коэффициентов уравнения (205) требуется выполнение условия (208). Условие (208) удобно формулировать следующим образом: произведение «внутренних» коэффициентов характеристического уравнения должно быть больше произведения «внешних» коэффициентов этого уравнения.
Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.
Термин употребляется также в применении к передаточной функции системы, записанной в виде преобразования Фурье выходного сигнала, поделённого на преобразование Фурье входного сигнала.
Система называется устойчивой
- если после снятия воздействия по окончании переходного процесса система возвращается в исходное равновесное состояние.
- если после изменения воздействия на постоянную величину, система переходит в новое равновесное состояние.
. (209)
Из анализа условий (207) … (209) следует, что для устойчивости системы управления, имеющей характеристическое уравнение (205), кроме положительности коэффициентов уравнения (205) требуется выполнение условия (208). Условие (208) удобно формулировать следующим образом: произведение «внутренних» коэффициентов характеристического уравнения должно быть больше произведения «внешних» коэффициентов этого уравнения.
Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики. По сути такой график объединяет на одной плоскости амплитудно-частотную и фазо-частотную характеристики.
Термин употребляется также в применении к передаточной функции системы, записанной в виде преобразования Фурье выходного сигнала, поделённого на преобразование Фурье входного сигнала.
Система называется устойчивой
- если после снятия воздействия по окончании переходного процесса система возвращается в исходное равновесное состояние.
- если после изменения воздействия на постоянную величину, система переходит в новое равновесное состояние.

 и
и  – эквивалентные коэффициенты передачи соответственно задающего и возмущающего воздействия. Они определяются по передаточным функциям эквивалентных звеньев, работающих в статическом режиме.
– эквивалентные коэффициенты передачи соответственно задающего и возмущающего воздействия. Они определяются по передаточным функциям эквивалентных звеньев, работающих в статическом режиме.







 , для мощности
, для мощности  , от частоты в логарифмическом масштабе.
, от частоты в логарифмическом масштабе. .
.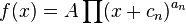 ,
,
 , то есть значение АЧХ, равное 100, превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
, то есть значение АЧХ, равное 100, превращается в 40 децибел шкалы ЛАЧХ. Если передаточная функция имеет вид:
 — комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:
— комплексная переменная, которую можно связать с частотой, используя следующую формальную замену:  ,
,  и
и  — константы, а
— константы, а  — передаточная функция. Тогда построить ЛАЧХ можно, используя следующие правила:
— передаточная функция. Тогда построить ЛАЧХ можно, используя следующие правила: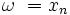 (ноль), наклон линии увеличивается на
(ноль), наклон линии увеличивается на  дБ на декаду.
дБ на декаду. (полюс), наклон линии уменьшается на
(полюс), наклон линии уменьшается на  дБ на декаду.
дБ на декаду. в передаточную функцию.
в передаточную функцию. , наклон меняется в точке
, наклон меняется в точке  сразу на
сразу на  дБ на декаду.
дБ на декаду. дБ выше линии (
дБ выше линии (  дБ для двух комплексно-сопряжённых нулей)
дБ для двух комплексно-сопряжённых нулей)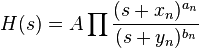

 положительно, начать линию (с нулевым наклоном) в 0 градусов,
положительно, начать линию (с нулевым наклоном) в 0 градусов, (
(  для комплексно сопряжённого) градусов на декаду начиная с
для комплексно сопряжённого) градусов на декаду начиная с  ,
, (
(  для комплексно сопряжённого) градусов на декаду начиная с
для комплексно сопряжённого) градусов на декаду начиная с  ,
, градусов для комплексно-сопряжённого нуля или полюса,
градусов для комплексно-сопряжённого нуля или полюса,