
|
|
Укрепление стенки поперечными рёбрами жесткости12
Так как местное напряжение присутствует (рис 2.4.) и
где С2 – коэффициент, принимаемый в зависимости от значения отношения
μ – отношение большей стороны к меньшей;
d – меньшая из сторон пластинки (
F – суммарная опорная реакция 2-х вспомогательных балок, опирающихся на главную балку
С1 – коэффициент, принимаемый в зависимости от значения отношения и значения: Следовательно
Из п.2.6 следует, что σ’= 22,59 кН/см2; τ’ = 4,99 кН/см2;
т.е. устойчивость не обеспечена. Принимаю решение изменить шаг поперечных ребер с as = 1,5 м, на as = 1,2 м
где С2 – коэффициент, принимаемый в зависимости от значения отношения
μ – отношение большей стороны к меньшей;
d – меньшая из сторон пластинки (
F – суммарная опорная реакция 2-х вспомогательных балок, опирающихся на главную балку
С1 – коэффициент, принимаемый в зависимости от значения отношения и значения: Следовательно Из п.2.6 следует, что σ’= 22,59 кН/см2; τ’ = 4,99 кН/см2;
т.е. устойчивость опять не обеспечена.
Принимаю решение изменить шаг поперечных ребер с as = 1,2 м, на as = 1,0 м Исходя, из принятого шага поперечных ребер можно сделать вывод, что местное напряжение отсутствует, и проверку местной устойчивости выполняю по формуле.
где Сcr – коэффициент, принимаемый в зависимости от значения
μ – отношение большей стороны к меньшей;
d – меньшая из сторон пластинки (
Из п.2.6 следует, что σ’= 22,59 кН/см2; τ’ = 4,99 кН/см2;
т.е. устойчивость обеспечена.
2.10. Расчёт опорного ребра Площадь сечения опорного ребра определяется из условия проверки его на смятие от опорной реакции балки (Qmax).
Принимаю th=14 мм.
Рис 2.5. Конструкция опорного ребра балки Производим расчёт на устойчивость
где Значение коэффициента φh определяем в зависимости от где
Катет угловых швов, прикрепляющих ребро к стенке
Принимаем kf = 6 мм. Расчёт центрально–сжатых сквозных колонн.
3.1. Подбор сечения стержня сквозной колонны Задаёмся значением коэффициента φ(0,7…0,9) φ=0,85, определяем требуемую площадь сечения по формуле
где N – продольная сила в колонне. N=2.Qmax=2.872.97=1745.9 кН
Принимаем два швеллера №30, для которых А=2.40,5= 81 см2, ix = 12 см. 3.1.1. Расчёт относительно материальной оси Вычисляем гибкость
где l – длинна колонны, l = 1200 – 0.9 – 27 – 130+50 = 1092.1 см; μ = 1.
Проверка устойчивости
Принимаем два швеллера №40, для которых А=2.61,5= 123 см2, ix = 15,2см. Повторяем расчет
Проверка устойчивости
Недонапряжение составит Так как имеем значительное недонапряжение, должны были бы принять меньшее сечение, но меньшее не проходит по устойчивости Окончательно принимаем два швеллера №40. 3.1.2. Расчёт относительно свободной оси Y Задаёмся λ1 = 40, тогда где λef = λ1 = 72,83 – из условия равноустойчивости.
Определяем требуемый радиус инерции
Приближённое расстояние между швеллерами
Принимаем b = 42 см
Вычисляем характеристики назначенного сечения (см рис 3.1.)
Вычисляем приведенную гибкость стержня
Проверка устойчивости
Недонапряжение составит Поскольку недонапряжение намного превышает 5%, изменим расстояние между швеллерами. Принимаем b= 27,5см
Вычисляем характеристики назначенного сечения (см рис 3.1.)
Вычисляем приведенную гибкость стержня
Проверка устойчивости
Недонапряжение составит 3.2. Расчёт планок Предварительно назначаем размеры планок: ширина ls = (0,5…0,75)b = 0.75b=20 см. Назначаем ls = 20 см. толщина ts = (1/10…1/25)ls = 1/20ls =1.0см. Назначаем ts = 1.0 см. расстояние между планками в свету Назначаем
Рис 3.1. Конструктивная схема сквозного сечения на планках Условная поперечная сила, приходящаяся на планку одной грани
Перерезывающая сила в планке
Изгибающий момент в планке
Момент сопротивления сечения планки
Проверяем прочность планки
Проверяем прочность сварных швов, прикрепляющих планку к ветвям по формуле.
где Задаёмся катетом швов kf = 8 мм; ручная сварка, βf = 0,7; Rwf= 18 кН/см2.
Прочность не обеспеченна. Задаёмся катетом швов kf = 10 мм; автоматическая сварка, βf = 1,1; Rwf= 21 кН/см2.
Прочность сварных швов обеспеченна. 3.3. Расчёт базы колонны База состоит из плиты и траверс. Требуемая площадь опирания плиты на фундамент
где N’ – продольная сила в колонне с учётом её собственной массы, N’ = N + G; G = 2.qветви.l.1,2 = 2.0,483.10,92.1,2 = 12,65 кН; qветви – масса 1 п.м. швеллера №40; 1,2 – коэффициент, учитывающий массу планок, оголовка и базы; Rф = 0,45 кН/см2 – расчётное сопротивление бетона фундамента (В 7.5);
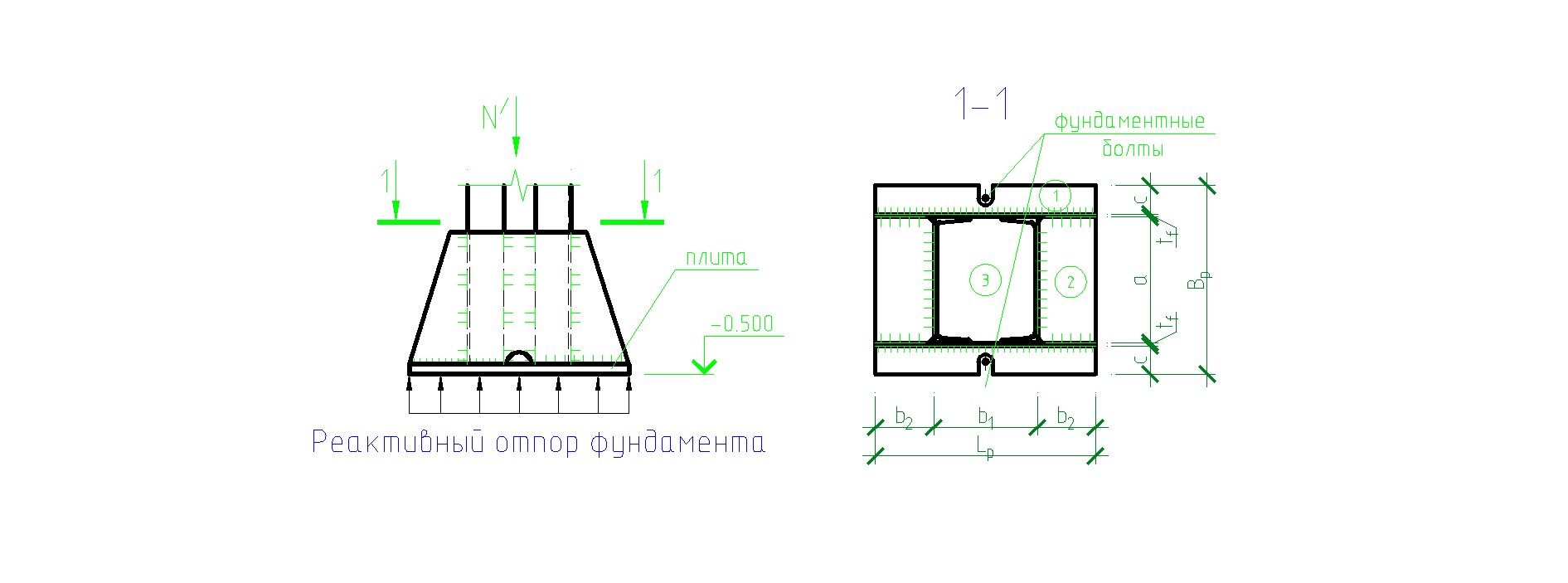
Рис 3.2. Конструкция базы колонны, шарнирно закреплённой в фундаменте N’ = N + G = 1745,9 + 12,65 = 1758,55 кН;
Задаёмся размером Вр = 2.с + 2.tt + а; с = (100…150) мм. Принимаем с = 10 см. tt = (8…12) мм. Принимаем tt = 1 см. Тогда Вр = 62 см, а размер Принимаем Lp = 65 см, b1 = 33 см, b2 = 8,5 см; тогда Вр = 62 см (рис 3.2.) Толщина плиты определяется по формуле
где М – максимальный изгибающий момент на участках плиты (рис 3.2.); Напряжение в бетоне фундамента будет
Участок №1. Плита работает как консольная балка
Участок №2. Плита работает как пластина, опертая на три стороны
где β2 – коэффициент для расчёта пластинки, опертой на три стороны. Участок №3. Плита работает как пластина, опертая на четыре стороны
где β3 – коэффициент для расчёта пластинки, опертой на четыре стороны; d – меньшая из сторон участка. Определяем толщину плиты
принимаем tp = 3,0 см.
3.4 Расчет траверсы колонны. Высоту траверса определяем по формуле
Задавшись катетом сварных швов kf = 8 мм
принимаем ht = 40 см. Расчётный катет швов, прикрепляющих траверсы и ветви к плите определяем по формуле
принимаем kf = 0,8 см Траверсу необходимо проверить на изгиб от реактивного давления фундамента по формуле
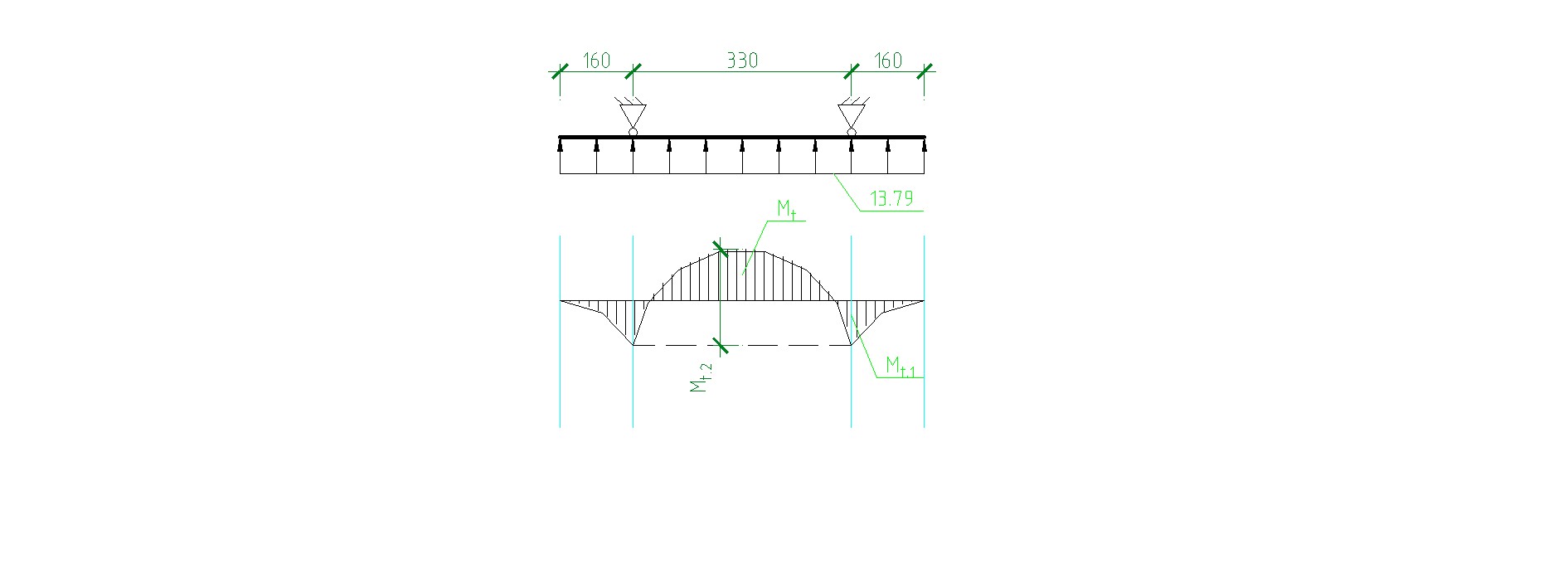
где Мt – максимальный изгибающий момент, определяемый как для двухпролётной балки (рис 3.3.)
Погонная нагрузка на треверсу
Рис 3.3. Расчётная схема траверсы
Момент сопротивления траверсы
Напряжение
3.5. Расчёт оголовка
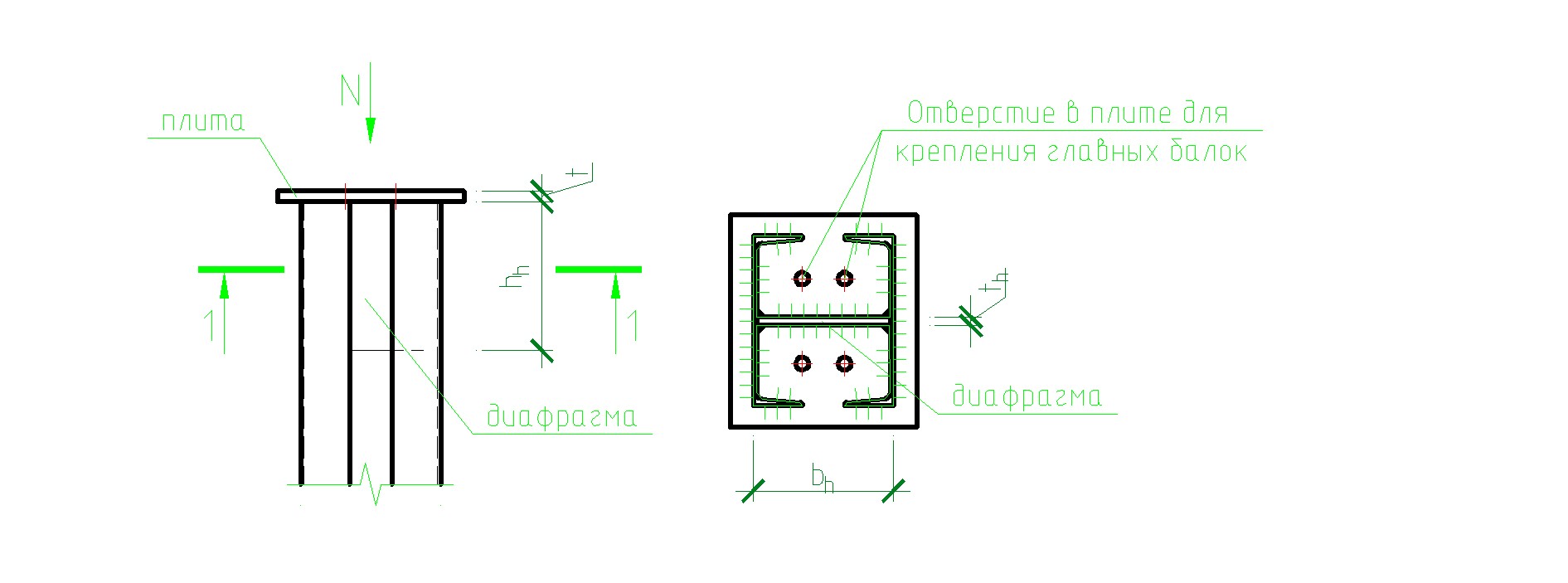
Рис 3.4. Конструкция оголовка колонны
Толщину плиты оголовка назначается без расчёта в пределах t = 20…25 мм. Принимаем t = 25 мм. Высота диафрагмы определяется длиной сварных швов, прикрепляющих диафрагму к ветвям. Задавшись катетом сварных швов 9 мм:
принимаем hh = 40 см. Толщина диафрагмы определяется из условия её работы на смятие
где Rp – расчётное сопротивление проката смятию торцевой поверхности; bh = b1 – 2.tw = 40 – 2.0,8 = 38,4
Проверяем прочность диафрагмы на срез
т.е. прочность не обеспеченна. принимаем th = 25 см Проверяем прочность диафрагмы на срез
т.е. прочность обеспеченна.
Библиографический список
1. Металлические конструкции. В 3 т. Т1. Элементы стальных конструкций / Под ред. В.В. Горева. –М.: Высшая школа, 1997.-527 с.
2. Металлические конструкции / Под общ. ред. Е.И.Беленя. – М.:Стройиздат,1975. – 424с.
3.Расчет конструкций балочной клетки: методические указания к курсовой работе по металлическим конструкциям /Липецкий государственный технический университет; Сост. В.М. Путилин, Н.В. Капырин. Липецк, 1999. 27с.
4.Расчет центрально-сжатых сквозных колонн: методические указания к курсовой работе по металлическим конструкциям /Липецкий государственный технический университет; Сост. В.М. Путилин, Н.В. Капырин. Липецк, 1999. 19с.
5.Строительные нормы и правила. Часть II. Нормы проектирования. Гл.23. Стальные конструкции (СниП II-23-81*). –М.: Стройиздат, 1988.-96с.
6.Свод правил СП 16,13330,2011 Стальные конструкции. Актуализированная редакция СниП II-23-81*

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , то необходима проверка устойчивости стенок балок по формулам:
, то необходима проверка устойчивости стенок балок по формулам: ,
, нормальное критическое напряжение.
нормальное критическое напряжение.


 касательное критическое напряжение
касательное критическое напряжение

 или
или  )
)





 =
= 
















 нормальное критическое напряжение.
нормальное критическое напряжение.





 Принимаем Аh = 23 см2.
Принимаем Аh = 23 см2. bh = bf’ = 180 мм – ширина опорного ребра;
bh = bf’ = 180 мм – ширина опорного ребра; 






 => φh = 0,932
=> φh = 0,932
 ,
,

 ,
, => φх = 0,557
=> φх = 0,557

 => φх = 0,708
=> φх = 0,708








 ;
; => φy = 0,623
=> φy = 0,623





 ;
; => φy = 0,587
=> φy = 0,587

 .
. 130 см
130 см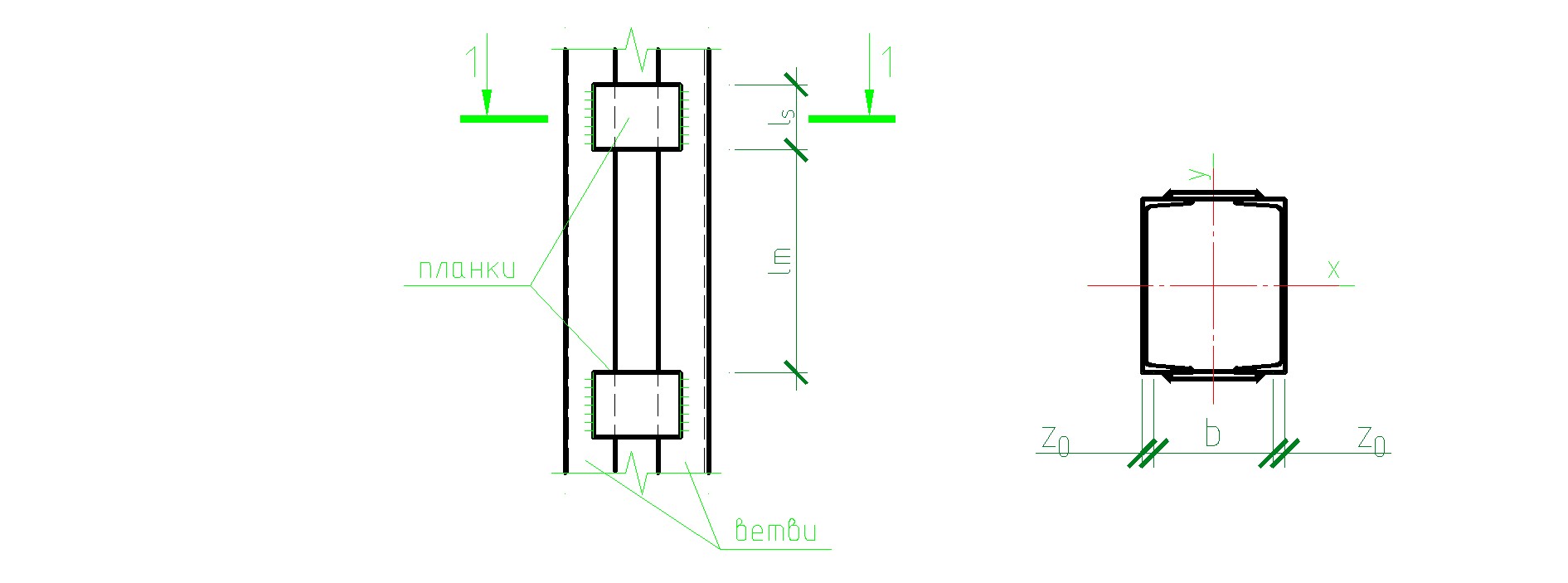






 ,
,















 .
.








 ,
, – момент сопротивления сечения траверсы.
– момент сопротивления сечения траверсы.







 принимаем th = 1,4 см
принимаем th = 1,4 см
