
|
|
Задача мультиклассовой классификации. Наивный Байесовский классификатор.Традиционная задача однометочной классификации, так же известной как мультиклассовой, ассоциирует объект x с единственным классом c из заранее известного конечного множества классов C. Однометочный набор данных D состоит из n элементов (x1, c1), (x2, c2), …, (xn, cn). Задача мультиклассовой классификации ассоциирует подмножество классов S⊆ C с каждым объектом. Следовательно, многоклассовый набор D представлен n элементами (x1, S1), (x2, S2), …, (xn, Sn). Задача мультиклассовой классификации получает повышенное внимание и актуальна для многих предметных областей, таких как классификация текстов и геномика.
Методы наивного Байеса – множество алгоритмов обучения с учителем, основанных на применении теоремы Байеса и предположении о независимости каждого признака. Теорема Байеса:
Из предположения о независимости признаков:
Для всех i выражение [1] может быть переписано в виде:
Так как знаменательиз [1] является постоянным, может быть использовано следующее правило классификации:
⇓
Проблема арифметического переполнения При достаточно большой длине документа приходится перемножать большое количество очень маленьких чисел. Для того чтобы при этом избежать арифметического переполнения снизу зачастую пользуются свойством логарифма произведения
Основание логарифма в данном случае не имеет значения. Проблема неизвестных слов С формулой [6] есть одна небольшая проблема. Если на этапе классификации встречается слово, которое не встречалось на этапе обучения, то значения Wic, а следственно и P(xi|c) будут равны нулю. Это приведет к тому что документ с этим словом нельзя будет классифицировать, так как он будет иметь нулевую вероятность по всем классам. Избавиться от этой проблемы путем анализа бóльшего количества документов не получится. Практически невозможно составить обучающую выборку, содержащую все возможные слова включая неологизмы, опечатки, синонимы и т.д. Типичным решением проблемы неизвестных слов является аддитивное сглаживание (сглаживание Лапласа). Идея заключается в предположении о том, что каждое слово встречается на один раз больше, то есть в прибавлении единицы к частоте каждого слова.
Логически данный подход смещает оценку вероятностей в сторону менее вероятных исходов. Таким образом, слова, не встречаемые на этапе обучения модели, получают пусть маленькую, но все же ненулевую вероятность. Подставив выбранные нами оценки в формулу [6] мы получаем окончательную формулу по которой происходит байесовская классификация:
В ходе выполнения курсового проекта была разработана реализация классификатора Naive Bayes для решения задачи многоклассовой классификации. За основу был взят алгоритм Multinomial Naive Bayes из библиотеки MLlib. Текущая реализация отличается поддержкой разреженных структур данных, что позволяет при тех же вычислительных ресурсах строить модели на обучающих выборках большего размера.
Предобработка данных Важным этапом курсового проекта является предобработка текстовых данных. Был разработан соответствующий программный код для системы Spark. Процесс предобработки условно может быть поделен на следующие этапы: 1. Удаление ссылок при помощи регулярных выражений; 2. Замена символа 'ё' на 'е'; 3. Замена небуквенных символов на символ пробела; 4. Замена последовательностей пробельных символов длины более 1 на один пробельный символ; 5. Разделение текста на слова (токенизация); 6. Удаление русских слов длинной более 15 и английских длиной более 25; 7. Удаление слов, содержащих символ '_'; 8. Фильтрация по спискам стоп-слов; 9. Стемминг. Стемминг — это процесс нахождения основы слова для заданного исходного слова. Основа слова необязательно совпадает с морфологическим корнем слова. Задача нахождения основы слова представляет собой давнюю проблему в области компьютерных наук.
Отбор признаков TF-IDF TF-IDF – метод векторизации признаков, широко применяемый в задачах при работе с текстовой информацией. Для определения уровня значимости терма в документе в контексте всего корпуса. Обозначим терм как t, документ как d и корпус как D. Частота термов TF(t,d) – это количество раз, которое терм t встречается в документе d, а частота документа DF(t,D) – количество документов, содержащих терм t. Если использовать лишь частоту термов для определения их важности, то легко переоценить термы, встречающиеся очень часто, но несущие мало информации о документе, например, "а", "и", "но". Если терм встречается очень часто во всём корпусе, это означает, что он не несет существенной информации о конкретном документе. Обратная частота документа - количественная мера информативности терма:
где |D| – общее число документов в корпусе. С момента использования логарифма, если терм встречается в каждом документе, то его значение IDF становится равным 0. TF-IDF - произведение TF и IDF:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

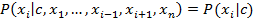
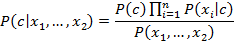


 . Так как логарифм – функция монотонная, её применение к обоим частям выражения изменит только его численное значение, но не параметры при которых достигается максимум. При этом, логарифм от числа близкого к нулю будет числом отрицательным, но в абсолютном значении существенно большим чем исходное число, что делает логарифмические значения вероятностей более удобными для анализа. Поэтому, мы переписываем нашу формулу с использованием логарифма.
. Так как логарифм – функция монотонная, её применение к обоим частям выражения изменит только его численное значение, но не параметры при которых достигается максимум. При этом, логарифм от числа близкого к нулю будет числом отрицательным, но в абсолютном значении существенно большим чем исходное число, что делает логарифмические значения вероятностей более удобными для анализа. Поэтому, мы переписываем нашу формулу с использованием логарифма.
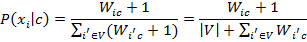

 ,
,