
|
|
Предельное разложение шеннона12 Предельное разложение Шеннона (k=n) булевой функции f(x1,x2,…,xn), не равной 0, имеет вид:
По k переменным
42. нахождение минимального покрытия таблицы Квайна. Покрытием таблицы Квайна -подмножество таких ее строк, которые в совокупности покрывают все столбцы таблицы. Длиной покрытия назовем количество строк, образующих покрытие. Рангом строки таблицы Квайна назовем ранг приписанной ей простой импликанты. Минимальным покрытием таблицы Квайна назовем покрытие с минимальной суммой рангов строк.Нетрудно видеть, что минимальное покрытие таблицы Квайна функции f(x1, …, xn) задает минимальную ДНФf. Таким образом, задача минимизации булевой функции решается построением таблицы Квайна и поиском минимальных покрытий. 43. найти отношение, обладающее свойствами рефлективности, симметричности, транзитивности. Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности. Примерами: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными). 46. максимальный интервал ФАЛ.Интервал I назовем максимальным для булевой функции f(x1, …, xn), если он является допустимым для этой функции, и не существует другого допустимого интервала I', такого что I 47. не полностью определенные ФАЛ и их минимизация .Подмножество FÌMy´Mx называется функцией, если для каждого элемента х, хÎ Mx найдется не более одного элемента уÎ My вида (х,у)ÎF, при этом ф-ия называется всюду( полностью определенной) , в протвном случае – частично определенной. реально на практике функции либо не определены полностью, либо есть запрещенные комбинации. Минимизировать неполностью определенную булеву функцию – это значит выбрать среди кратчайших ДНФ всех ее доопределений самую короткую ДНФ. Пусть заданна ф-ия f()=
48. таблица истинности функции сложение по модулю 2 и дизъюнкция Сложение по модулю 2 (исключающее ИЛИ, в просторечье XOR) - определяет результат сравнения двух простых логических выражений А и В. Результатом является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения различны.11-0;10-1;01-1;00-0. Логическое сложение (дизъюнкция, логическое ИЛИ) - это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Обозначение: или + 11-1;10-1;01-1;00-0
50. минимизация ФАЛ методом КВАйна – Мак – Класки. 1) нахождение первичных импликант. Все минетермы ф-ии сравниваются между собой попарно. Если минитемы mi и mj таковы, что имеют вид ахi и анехi то выписывается конъюнкция а, являющаяся минетерном ахi и анехi.. минетерны н-го ранга , для которых произошло склеивание отмечаем. Строим минетерны (n-1)-го порядка , опять сравниваем их и т.д. заканчиваются склеиания тогда когда минетермы уже не сравниваются. Все не отмеченные минетермы называются первичные или просте. 2) составляем таблицу, число строк которой равно числу первичных импликант , число столбцов – число минетернов. На пересечение покрываемых ставим метку. 3) выбираем минимальное покрытие. Выбираем совокупность имплекант, которые включают метки во всех столбцах. 54. какие из элементарных ФАЛ сохраняют константой 1.Булева функция сохраняет константу 1 (принадлежит классу T1), если на наборе из всех единиц функция принимает значение единица. Это ф-ии: дизъюнкция и конъюнкция, импликация и эквивалентность. 55. универсальное мн-во – это такое мн-во которое состоит из всех эл-ов а так же подмножеств множества объектов исследуемой области. 56. свойство отношения следствия и строгого следствия. отношение логического следования рефлексивно, транзитивно. 57. фактор множество множества М по заданному отношению R. Фактор множеств- совокупность классов эквивалентности этого множества. Множество окрестностей единичного радиуса, взятых для всех эл-ов мн-ва М при задании в нем отношения R2ÌM2, называется фактором-множеством M/R2мн-ва М по отношению R2. Фактор-мн-во M/R2 полностью оредел отношение R2. 61.таблица истинности функции импликации и конъюкции Логическое следование (импликация) - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. 11-1;10-0;01-1;00-1. 62. свойство линейности ФАЛ.Функция f(x1,x2..xn) называется линейной если существуют такие а0,а1,а2...аn где аiÎ{0,1}, "i=от 1 до n, что для любых x1,x2..xn имеет место равенство: f(x1,x2..xn)= а0Åа1×х1Åа2×х2Å...Åan×xn 63. свойство отношения делимости.Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя. Отношение делимости антисимметрично, т.е. если 64. множество подмножеств множества.Множество А является подмножеством множеств В, если любой элемент принадлежащий А, так же принадлежит В. (АÌВ)Û(хÎА®хÎВ) 67. построение СДНФ по таблице истиностиПостроение СДНФ по таблице истинности: 1) Выбрать из таблицы истинности те строки, в которых значение формулы - "Истина" (1). 2) Для каждой выбранной строки составить конъюнкцию переменных или их отрицаний так, чтобы эта конъюнкция была истинной (для этого переменные, которые в соответствующей строке имеют значение "Ложь" (0) нужно взять с отрицанием, а переменные, имеющие значение "Истина" (1) - без отрицания). 3) Составить дизъюнкцию полученных конъюнкций. 68.декартово произведение множеств и отношений.Декартовым произведением множеств называют мн-во эл-ов, которые являются всевозможнвми последовательностями, такие что 1 элемент пренадлежит первому мн-ву , второй второму мн-ву, и т.д. мощность декартового произведение равна произведению пощностей сомножетеля. |M1´M2´..Mn|=|M1|*|M2|…|Mn| Декартово произведение RxS двух отношений определяет новое отношение - результат конкатенации (т.е. сцепления) каждой записи из отношения R с каждой записью из отношения S. 69. построение таблицы истинности.Алгоритм 1)Определить количество строк: количество строк = 2n + строка для заголовка, n - количество простых высказываний. 2)Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; определить количество переменных (простых выражений); определить количество логических операций и последовательность их выполнения.3)тЗаполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций. 75.Операция дополнения множества и закон двойного отрицания. Пусть множество А и В таковы, что А 80. свойство идемпотентности конъюнкции и дизъюнкции.АÚА..ÚА=А; АÙАÙ…ÙА=А 81. выполнение операций с универсальным и пустым множествами. АÈÆ=А,A ∩ ∅ = ∅, A ∪ I = I, A ∩ I = A, A ∪ A = I , A ∩ A = ∅, А\Æ=А, Æ\А=Æ, не A = I \ A, А´Æ=Æ, Æ´А=Æ, А¸Æ=А, А¸Æ=А 82. операции дизъюнкции и конъюнкции с константами 0 и 1AÙ1 = A, AÙ0 = 0, A∨1 = 1, A∨0 = A 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
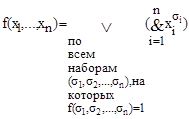 Предельное разложение Шеннона булевой функции f(x1,x2,…,xn) является ее СДНФ. В алгебре Буля справедлив принцип двойственности, согласно которому имеем следующие двойственные разложения Шеннона булевой функции f(x1,x2,…, xk , xk+1,… ,xn):
Предельное разложение Шеннона булевой функции f(x1,x2,…,xn) является ее СДНФ. В алгебре Буля справедлив принцип двойственности, согласно которому имеем следующие двойственные разложения Шеннона булевой функции f(x1,x2,…, xk , xk+1,… ,xn):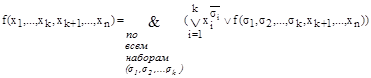
 I'. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.
I'. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.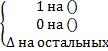 от неполно определенной ф-ии строятся две ф-ии, нулевого определения и единичного доопределения. После этого нахадится лин покрытие конституент един ф-и нулевого определения и ф-ии единичного доопределения. Вместо неопределенностей подставляем 1 решаем методом Квайна-МАК-Класки.
от неполно определенной ф-ии строятся две ф-ии, нулевого определения и единичного доопределения. После этого нахадится лин покрытие конституент един ф-и нулевого определения и ф-ии единичного доопределения. Вместо неопределенностей подставляем 1 решаем методом Квайна-МАК-Класки. и
и 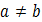 , то
, то  . Отношение делимости транзитивно, т.е. если
. Отношение делимости транзитивно, т.е. если 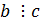 , то
, то 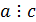 .
.  В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:
В. Тогда дополнением множества А до множества В называется разность В\А. В этом случае применяется обозначение СBА=В\А. Если в качестве множества В берётся универсальное множество U, то применяется обозначение СА=СUА=U\А и такое множество просто называют дополнением множества А. Таким образом, символическая запись определения дополнения множества будет следующей:  СА={x | x
СА={x | x 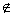 A}. закон двойного отрицания можно сформулировать так: отрицание отрицания дает утверждение, или: повторенное дважды отрицание дает утверждение. ~~ А → А,
A}. закон двойного отрицания можно сформулировать так: отрицание отрицания дает утверждение, или: повторенное дважды отрицание дает утверждение. ~~ А → А,