
|
|
Задачи теории игр в экономике. Доминируемые и доминирующие стратегии. Седловая точка. Решение игр в чистых стратегиях.Система линейных алгебраических уравнений. Линейные операторы и матрицы. Система m линейных уравнений с n неизвестными (
Или в матричной записи: AX=B, где Рангом матрицы системы А называется ранг системы векторов, образуемых строками матрицы. Пусть V – линейное пространство. Если указано правило, по которому каждому вектору Определение: Отображение f линейного пространства V в себя называется линейным преобразованием (линейным оператором), если для любых векторов
Из этих условий следует, что действие линейного преобразования f на линейную комбинацию нескольких векторов подчиняется формуле Примеры линейных преобразований: 1. Нулевое преобразование: 2. Тождественное преобразование: 3. Проектирование на n-мерное подпространство, порожденное системой векторов базиса: Пусть Определение: Подмножество векторов линейного пространства V таких, что Пример: Для примера 3 ядром линейного преобразования является линейная оболочка Пусть дана СЛАУ (запись линейного преобразования в координатах): Доходность и риск финансовой операции. Функция полезности инвестора. Кривая безразличия. Оптимальный портфель. Вогнутая функция полезности случайного дохода и отрицательное отношение к риску. Функция полезности (ФП)— экономическая модель для определения предпочтений экономических субъектов. Функции полезности имеют пять основных свойств: 1. ФП инвариантны относительно положительных линейных преобразований. То есть функция полезности, подвергнутая воздействию положительной константы, приведет к выбору тех же самых инвестиций. 2. ненасыщением. Другими словами, фп никогда не приведет к предпочтению меньшего капитала большему при достоверных исходах или равенстве их вероятностей. Поскольку при росте капитала должна расти и полезность, то первая производная от полезности как функции капитала должна быть положительной 3. Три типа отношения инвестора к риску (нерасположенность к риску). Он может либо уклоняться от риска, либо быть нейтральным к нему, либо жаждать риска. Неприятие риска характеризуется второй производной функции предпочтения полезности U"(x). У индивидуума, уклоняющегося от риска, вторая производная отрицательна, у склонного к риску – положительна, а у нейтрального к риску – вторая производная функции предпочтения риска нулевая. На рис. изображены три основных типа функций предпочтения полезности в зависимости от U"(x), или степени неприятия риска инвестора. 4. как изменяется степень неприятия риска инвестора при изменении капитала. При этом говорят об абсолютной величине нерасположенности к риску. Здесь вновь имеются три категории индивидуумов: 1) возрастающее абсолютное неприятие риска. По мере роста капитала они держат все меньше средств в рискованных активах. 2) с постоянным абсолютным неприятием риска. С ростом капитала они сохраняют те же денежные вложения в рискованные активы. 3) понижение абсолютного неприятия риска. С ростом капитала они готовы держать больше денег в рискованных активах.
Задачи теории игр в экономике. Доминируемые и доминирующие стратегии. Седловая точка. Решение игр в чистых стратегиях. Во многих задачах финансово-экономической сферы возникает необходимость принятия решения. Проблема принятия решения осложняется тем, что ее приходится решать в условиях неопределенности (необходим количественный анализ ситуаций). Математические методы обоснования решений дают возможность анализа вариантов решения с целью уменьшения риска, которое иногда достигается за счет получения дополнительной информации. Математизация содержательных финансово-экономических задач о принятии решениях в условиях неопределенности приводит к соответствующим экономико-математическим моделям и методам, теоретический аспект которых составляет теорию игр. Пример:Конкурирующие на одном рынке фирмы осуществляющие действия, приводящие к реализации своих интересов и препятствующие в этом конкурентам. 1.Наличие конфликтной ситуации 2.Математическая модель конфликтной ситуации – игра.3.Заинтересованные стороны – игроки. 4.Коалиции Любое возможное действие игрока – чистая стратегия.Игра конечная, если множество стратегий каждого игрока конечное. Игрок А обладает m В условиях конфликта каждый игрок делает свой ход, т.е. выбирает одну из своих чистых стратегий. В результате чего образуется набор x = ( Матрица выигрышей: Если каждый игрок A и B сознательно определенным образом выбирает свои чистые стратегии Рассмотрим 2 смешаные стратегии игрока А: [Рассмотрим 2 смешаные стратегии игрока B: 1) 2) 3) 4) 5) 6) Если k-я строка матрицы игры нестрого (строгое) доминируется некоторой выпуклой комбинацией остальных ее строк, то k-ю строку можно (нужно) удалить. Ситуация (Ai0, Bj0) называется равновесной, или ситуацией равновесия, или устойчивой, или седловой точкой игры, если она удовлетворительная для каждого из игроков А и В. Таким образом, элемент Стратегии Ai0 иBj0игроков А и В, создающие равновесную ситуацию (Ai0, Bj0), или, другими словами, соответствующие седловой точке
Совокупность{ Решение игры характеризуется тем свойством, что ни одному из игроков, придерживающихся одной их своих оптимальных стратегий, невыгодно от нее отклонится, поскольку в этом случае он не увеличит своего выигрыша. 46. Структурное программирование на языке С++. Понятие класса и объекта. Поля и методы класса. Конструкторы и деструкторы. Шаблоны классов. Выбор структур данных должен предшествовать созданию алгоритмов. Память под данные выделяется либо на этапе компиляции (в этом случае необходимый объем должен быть известен до начала выполнения программы, то есть задан в виде константы), либо во время выполнения программы с помощью операции ne w или функции mallос (необходимый объем должен быть известен до распределения памяти). В обоих случаях выделяется непрерывный участок памяти. Если до начала работы с данными невозможно определить, сколько памяти потребуется для их хранения, память выделяется по мере необходимости отдельными блоками, связанными друг с другом с помощью указателей. Такой способ организации данных называется динамическими структурами данных, поскольку их размер изменяется во время выполнения программы. Они различаются способами связи отдельных элементов и допустимыми операциями. Динамическая структура может занимать несмежные участки оперативной памяти. Динамические структуры широко применяют и для более эффективной работы с данными, размер которых известен, особенно для решения задач сортировки, поскольку упорядочивание динамических структур не требует перестановки элементов, а сводится к изменению указателей на эти элементы. Элемент любой динамической структуры данных представляет собой структуру (в смысле struct), содержащую по крайней мере два поля: для хранения данных и для указателя. Полей данных и указателей может быть несколько. Поля данных могут быть любого типа: основного, составного или типа указатель. Класс — разновидность абстрактного типа данных в (ООП), характеризуемый способом своего построения. Отличия классов от других абстрактных типов данных: при задании типа данных класс определяет одновременно и интерфейс, и реализацию для всех своих экземпляров, а вызов метода-конструктора обязателен. На практике ООП сводится к созданию некоторого количества классов, включая интерфейс и реализацию, и последующему их использованию. Идея классов пришла из работ по искусственному интеллекту. Любую вещь всегда можно представить частным случаем некоторого более общего понятия. Объект в программировании — некоторая сущность в виртуальном пространстве, обладающая определённым состоянием и поведением, имеющая заданные значения свойств (атрибутов) и операций над ними (методов). Как правило, при рассмотрении объектов выделяется то, что объекты принадлежат одному или нескольким классам, которые определяют поведение (являются моделью) объекта. Термины «экземпляр класса» и «объект» взаимозаменяемы. Поле класса или атрибут — переменная, связанная с классом или объектом. Все данные объекта хранятся в его полях. Доступ к полям осуществляется по их имени. Обычно тип данных каждого поля задаётся в описании класса, членом которого является поле. Каждый объявляемый класс должен предусматривать КОНСТРУКТОР для инициализации объекта класса при его создании. Он является специальным методом (элемент-функцией), которая должна определяться с тем же именем, что и класс, чтобы компилятор мог отличить ее от других методов класса. C++ требует вызова конструктора при создании каждого объекта, что помогает гарантировать инициализацию объекта до того, как он будет использоваться в программе. Отличие конструкторов от методов класса - конструкторы не могут возвращать значений и потому не могут специфицировать возвращаемый тип (даже void). Обычно конструкторы объявляются как public. Конструктор, не принимающий аргументов, является конструктором по умолчанию. В любом классе, не имеющем конструктора, компилятор генерирует конструктор по умолчанию. Функцией-членом, выполняющей действия, обратные конструктору, является деструктор. Этот метод (функция-член) вызывается при удалении объекта. Он выполняет работу по освобождению памяти, занятой объектом, имеет то же имя, что и класс, которому он принадлежит, с предшествующим символом ~ и не имеет возвращаемого значения. Шаблон - это предписание для создания класса, в котором один или несколько типов либо значений параметризованы. Используя ключевое слово template и символы типов (например, Т, T1 и Т2) программы могут создать шаблон класса — определение шаблона класса может использовать эти символы для объявления элементов данных, указания типов параметров и возвращаемого значения функций-элементов и т.д. Для создания объектов класса с использованием шаблонов программы просто ссылаются на имя класса, за которым внутри угловых скобок следуют типы (например, <int, float>), каждому из которых компилятор назначает символы типов и имя переменной. Шаблоны классов помогут избавиться от дублирования кода программы, если необходимы объекты похожих классов, которые отличаются только типом. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ) записывается в общем виде так:
) записывается в общем виде так:
 ,
,  ,
,  .
. из V ставится в соответствие единственный вектор
из V ставится в соответствие единственный вектор  из V, то будем говорить, что задано отображение пространства V в себя, или преобразование пространства V.
из V, то будем говорить, что задано отображение пространства V в себя, или преобразование пространства V. и для любого
и для любого  выполняются равенства:
выполняются равенства: и
и 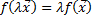 .
. , а также
, а также  .
. .
. .
. – базис линейного пространства V и
– базис линейного пространства V и  – разложение произвольного вектора по базису. Положим
– разложение произвольного вектора по базису. Положим  – линейное преобразование.
– линейное преобразование. , а образом -
, а образом -  .
. или в матричном виде Y+AX. Матрица А называется матрицей линейного преобразования.
или в матричном виде Y+AX. Матрица А называется матрицей линейного преобразования.
 Математически абсолютное неприятие риска
Математически абсолютное неприятие риска  Если нужно узнать, как изменяется абсолютное неприятие риска с изменением капитала, то мы берем первую производную от А(х) по х (капитал) – А'(х). При этом у индивидуума с возрастающим абсолютным неприятием риска было бы А'(х) > 0, при постоянном абсолютном неприятии риска было бы А'(х) = 0, а при понижающемся абсолютном неприятии риска было бы А'(х) < 0.
Если нужно узнать, как изменяется абсолютное неприятие риска с изменением капитала, то мы берем первую производную от А(х) по х (капитал) – А'(х). При этом у индивидуума с возрастающим абсолютным неприятием риска было бы А'(х) > 0, при постоянном абсолютном неприятии риска было бы А'(х) = 0, а при понижающемся абсолютном неприятии риска было бы А'(х) < 0. 1 чистыми стратегиями обозначим
1 чистыми стратегиями обозначим 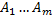 , а множество этих стратегий
, а множество этих стратегий  .
.  . Для B:
. Для B: 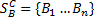 , где
, где  1 .
1 . стратегий всех игроков – исход или ситуация конфликта. Множество всех ситуаций в чистых стратегиях:
стратегий всех игроков – исход или ситуация конфликта. Множество всех ситуаций в чистых стратегиях: 
 соответственно, то сложившаяся ситуация
соответственно, то сложившаяся ситуация  однозначно определяет выигрыш игрока А, определяющийся числом
однозначно определяет выигрыш игрока А, определяющийся числом 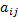 , одновременно являясь проигрышем (-
, одновременно являясь проигрышем (- 
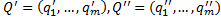 ]
]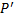 доминирует
доминирует  (
(  , если
, если  , j=1,..,n
, j=1,..,n , если
, если  , j=1,..,n
, j=1,..,n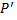 называется эквивалентной (дублирующей)
называется эквивалентной (дублирующей) 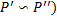 , если
, если  , j=1,..,n
, j=1,..,n доминирует
доминирует  (
(  , если
, если 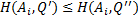 , i=1,..,m
, i=1,..,m , если
, если  , i=1,..,m
, i=1,..,m называется эквивалентной (дублирующей)
называется эквивалентной (дублирующей)  , если
, если  , i=1,..,m
, i=1,..,m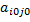 , являющийся седловой точкой матрицы игры, является минимальным в своей строке и максимальным в своем столбце.
, являющийся седловой точкой матрицы игры, является минимальным в своей строке и максимальным в своем столбце. и
и  – множества чистых оптимальных стратегий соответственно игроков А и В. Если нижняя цена игры α равны верхней цене β, то их общее значение γ=α=β называется ценой игры в чистых стратегиях.
– множества чистых оптимальных стратегий соответственно игроков А и В. Если нижняя цена игры α равны верхней цене β, то их общее значение γ=α=β называется ценой игры в чистых стратегиях.