|
Условие, при котором две прямые лежат в одной плоскости
Справочные материалы Аналитическая геометрия
Вектора

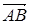 = (x2 –x1; y2–y1; z2–z1) = (x2 –x1; y2–y1; z2–z1)
Длина вектора
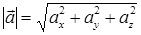 или или 
Направляющие косинусы вектора

Единичный вектор

Орт вектора 


| Скалярное произведение
| Векторное произведение
| Смешанное произведение
| Число
 × × 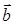 = ï = ï  ïï ïï 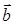 ïcosj ïcosj

| Вектор

 ´ ´ 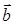 = = 
| Число

| Свойства:
1)  × ×  = ï = ï  ï2;
2) ï2;
2)  × × 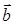 = 0, если = 0, если  ^ ^ 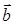 ;
3) ;
3)  × × 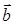 = = 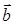 × ×  ; ;
| Свойства:
1)  ;
2) ;
2) 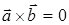 , если , если  ïï ïï 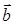
| Свойства:
1)  2)
2) 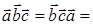  3)
3)  , если вектора компланарны , если вектора компланарны
| Приложения:
Угол между векторами
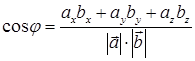 Проекция вектора на вектор
Проекция вектора на вектор

| Приложения:
Площадь параллелограмма

| Приложения:
Объем параллелепипеда и пирамиды
V =  Vпир =
Vпир = 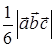
|
Прямая на плоскости
Основные типы уравнений прямых на плоскости
| Название
| Уравнение
| Что дано
| Иллюстрация
| | Общее
| Ах + Ву + С = 0
|
| Коэффициенты А и В – координаты нормального вектора 
| | С угловым
коэффициентом
| 
|  угловой коэффициент k или угол наклона α
угловой коэффициент k или угол наклона α
|  – угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ – угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ

| | В данном
направлении
| 
|  ,
угловой коэффициент k или угол наклона α ,
угловой коэффициент k или угол наклона α
| 
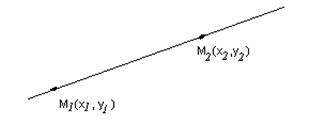
| | Через две точки
| 
| 

| 
| | В отрезках
| 
| Прямая отсекает на координатных осях отрезки a и b
| 
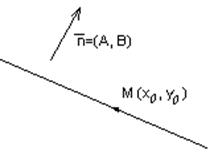
| | Перпендикулярно
вектору
| 
| 

|  – нормальный вектор – нормальный вектор
| | Каноническое
| 
| 

|  – направляющий вектор – направляющий вектор

| | Полярное
| 
| р – расстояние от начала координат до прямой, 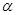 – угол отклонения перпендикуляра р от координатной оси – угол отклонения перпендикуляра р от координатной оси
| 
| | Нормальное
| 
| р – расстояние от начала координат до прямой, 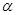 – угол отклонения перпендикуляра р от оси ОХ – угол отклонения перпендикуляра р от оси ОХ
| Нормирующий множитель
 (общее→нормальное)
(общее→нормальное)

|
Основные задачи на плоскости
1. Расстояние между точками 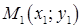 и и 

2. Площадь треугольника с вершинами в точках 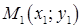 , ,  , , 

3. Деление отрезка в данном отношении λ

4. Угол  между прямыми между прямыми  и и 
 

5. Параллельность и перпендикулярность прямых
  
6. Расстояние от точки  до прямой до прямой 
 : Ах + Ву + С = 0 : Ах + Ву + С = 0

Основные виды кривых второго порядка на плоскости
| Название кривой
| Вид уравнения
| Основные сведения о кривой
| Вид кривой
| | Окружность
| 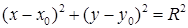
| R – радиус
Центр в точке 
| 
| | Эллипс
| 
| a – большая полуось,
b – малая полуось
Вершины эллипса А(а; 0), А’(–a; 0), В(0; b), В’(0; –b)
с – фокусное расстояние,  Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет,
Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет, 
| 
| | Гипербола
| 
| a – действительная полуось,
b – мнимая полуось
Вершины гиперболы А(а; 0), А’(–a; 0),
с – фокусное расстояние,  Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет,
Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет, 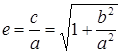 Асимптоты
Асимптоты 
| 
| | Парабола
| 
| р – параметр параболы
ОХ – ось симметрии
Фокус F(р/2; 0)
Директриса y = –p / 2
| 
| 
| р – параметр параболы
ОУ – ось симметрии
Фокус F(0; р/2),
Директриса y = –p / 2
| 
|
Уравнение 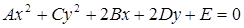 всегда определяет: всегда определяет:
– окружность, при А = С,
– эллипс, при АС>0,
– гиперболу, при АС<0,
– параболу, при АС = 0.
При этом возможны случаи вырождения:
– для эллипса (окружности) – в точку или мнимый эллипс (окружность);
– для гиперболы – в пару пересекающихся прямых;
– для параболы – в пару параллельных прямых.
Прямая и плоскость в пространстве
Основные типы уравнения плоскости в пространстве
| Название уравнения
| Вид уравнения
| Что дано
| Примечание
| | Общее уравнение плоскости
| 
|
|  – нормальный вектор плоскости или нормаль – нормальный вектор плоскости или нормаль
| | Уравнение плоскости, проходящее через заданную точку, перпендикулярно данному вектору
| 
|  ,
нормаль ,
нормаль  . .
|  – произвольная точка – произвольная точка

| | Уравнение плоскости, проходящей через три точки
| 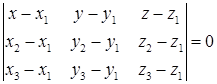
| 
|  – произвольная точка – произвольная точка

| | Уравнение плоскости в отрезках
| 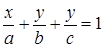
| а – по Ox,
b – по Оу,
с – по Оz.
Отрезки, отсекаемые плоскостью на осях координат
| 
| | Нормальное уравнение плоскости
| 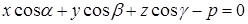
| р – расстояние от начала координат до плоскости
 – углы, образованные вектором – углы, образованные вектором  с осями Ox, Oy, Oz. с осями Ox, Oy, Oz.
|  – единичный вектор, направленный по перпендикуляру ОК = р, опущенному на плоскость из начала координат – единичный вектор, направленный по перпендикуляру ОК = р, опущенному на плоскость из начала координат

|
Основные типы уравнения прямой в пространстве
| Название уравнения
| Вид уравнения
| Что дано
| Примечание
| | Общее уравнение прямой
| 
|
| 
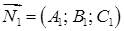 и и  – нормали пересекающихся плоскостей – нормали пересекающихся плоскостей
| | Векторное уравнение прямой
| 
|  ,
направляющий вектор ,
направляющий вектор  , параллельный прямой , параллельный прямой 
| 
 произвольная точка на прямой, произвольная точка на прямой,  , , 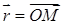 . .
| | Параметрическое уравнение прямой
| 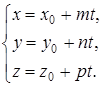
|  ,
направляющий вектор ,
направляющий вектор  , параллельный прямой , параллельный прямой 
|  – параметр – параметр

| | Канонические уравнения прямой
| 
|  ,
направляющий вектор ,
направляющий вектор  , параллельный прямой , параллельный прямой 
| 
| | Уравнение прямой, проходящей через две точки
| 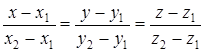
| 

| 
|
Основные задачи в пространстве
Угол между плоскостями
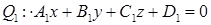 , , 
 , , 

Параллельность и перпендикулярность плоскостей
Если   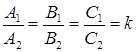
Если      
Расстояние от точки до плоскости
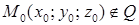 , ,
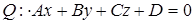 . .

Угол между двумя прямыми
 
 

Условие параллельности и перпендикулярности прямых в пространстве
Если    . .
Если      
Условие, при котором две прямые лежат в одной плоскости
  , , 
  , , 
Тогда 
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



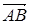 = (x2 –x1; y2–y1; z2–z1)
= (x2 –x1; y2–y1; z2–z1)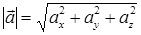 или
или 





 ×
× 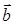 = ï
= ï 



 ;
2)
;
2) 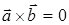 , если
, если  2)
2) 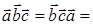
 3)
3)  , если вектора компланарны
, если вектора компланарны
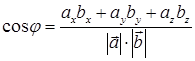 Проекция вектора на вектор
Проекция вектора на вектор


 Vпир =
Vпир = 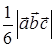


 угловой коэффициент k или угол наклона α
угловой коэффициент k или угол наклона α
 – угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ
– угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ


 ,
угловой коэффициент k или угол наклона α
,
угловой коэффициент k или угол наклона α












 – направляющий вектор
– направляющий вектор


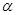 – угол отклонения перпендикуляра р от координатной оси
– угол отклонения перпендикуляра р от координатной оси


 (общее→нормальное)
(общее→нормальное)

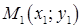 и
и 




 между прямыми
между прямыми  и
и 






 до прямой
до прямой 

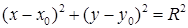



 Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет,
Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет, 


 Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет,
Фокусы F1(c; 0), F2(–c; 0)
e – эксцентриситет, 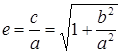 Асимптоты
Асимптоты 





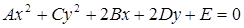 всегда определяет:
всегда определяет:
 – нормальный вектор плоскости или нормаль
– нормальный вектор плоскости или нормаль

 ,
нормаль
,
нормаль  .
.
 – произвольная точка
– произвольная точка

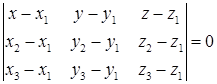


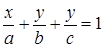

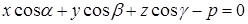
 – углы, образованные вектором
– углы, образованные вектором  с осями Ox, Oy, Oz.
с осями Ox, Oy, Oz.
 – единичный вектор, направленный по перпендикуляру ОК = р, опущенному на плоскость из начала координат
– единичный вектор, направленный по перпендикуляру ОК = р, опущенному на плоскость из начала координат



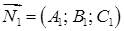 и
и  – нормали пересекающихся плоскостей
– нормали пересекающихся плоскостей

 ,
направляющий вектор
,
направляющий вектор  , параллельный прямой
, параллельный прямой 

 произвольная точка на прямой,
произвольная точка на прямой,  ,
, 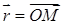 .
.
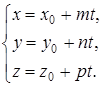

 – параметр
– параметр


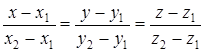



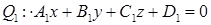 ,
, 
 ,
, 



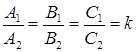





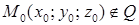 ,
,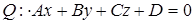 .
.







 .
.





