
|
|
Влияние германия на радиационные свойства кремния12 Облучение кремния быстрыми электронами или γ–лучами позволяет вводить в кристалл первичные дефекты – пары Френкеля, вакансии, междоузельные атомы, небольшие их скопления. В исследованиях радиационных дефектах в кремнии применяется гамма облучение и облучение электронами. Первичные радиационные дефекты имеют большую подвижность, что обусловливает эффективное взаимодействие их между собой и другими дефектами кристалла, так в процессе миграции вакансий образуют комплексы со многими примесями замещения, взаимодействуют между собой с образованием дивакансий и сложных вакансионных комплексов.
Сравнительное исследования влияния облучения быстрыми электронами на физические свойства монокристаллов кремния, легированных и нелегированных германием показало, что процессы образования дефектов в монокристаллах кремния, легированных германием, протекает не так, как в нелегированном кремнии.
Скорость восстановления (после отжига) концентрации основных носителей заряда в монокристаллах Si выше, чем в монокристаллах Si<Ge>. Введение германия несколько повышает радиационную стойкость по относительному изменению времени жизни неосновных носителей заряда.
Скорость восстановления (после отжига) времени жизни неосновных носителей заряда выше монокристаллах Si<Ge>. Скорость образования А-центров при облучении в монокристаллах Si выше, чем в Si<Ge>. Замедление формирования А-центров в облученных монокристаллах Si<Ge> говорит о процессах «внутреннего» гетерирования.
Воздействия германия на первичное дефектообразование происходит за счёт упругой деформации, вызванной его ведением. Происходит уменьшение энтальпии образования пар Френкеля и тем самым увеличивается их концентрация.
Введение германия существенно понижает эффективность образования радиационных дефектов в кремнии, что обусловлено непрямой иннигиляцией вакансий и собственных междоузельных атомов через примесные центры. При низких температурах атомы германия, обладая большим, чем атомы матрицы, ковалентными тетраэдрическим радиусом, являясь эффективными ловушками вакансий, образуя комплексы [GeV], отжигающиеся в интервале температур 200 – 280 К.
Влияние германия на процессы первичного дефетообразования происходит за счёт упругой деформации, вызванной введением изовалентной примеси при её неоднородном распределении.
Кинетика изохронного отжига радиационных дефектов зависит от содержания германия в монокристаллах кремния. Примесные атомы германия, при выращивании, образуют кластеры переменного размера, вследствие чего варьируются упругие напряжения в решётке кремния.
С ростом NGe уменьшаются флуктуации в размерах кластеров германия, большинство их становится примерно одинаково размера и отжиг дефектов, связанных с Ge происходит не в две стадии, а на одной.
Введение германия в монокристаллы кремния n-типа проводимости не влияет на энергетический спектр радиационных дефектов при облучении гамма-квантами, их кинетику накопления, изменения времени жизни неосновных носителей заряда, легирование кремния германием не влияет на процессы отжига и перестройку радиационных дефектов.
Присутствие германия в кремнии (в особенности при больших концентрациях) замедляет генерацию дивакансий и изменяет характер их отжига. Концентрация А-центров не зависит от концентрации германия. Следовательно, упругие напряжения, возникающие в кремнии из-за присутствия атомов германия, уменьшают концентрацию вакансий, возникающих при облучении в области каскада соударений, и способствуют накоплению междоузельных атомов в кристалле кремния.
Атомы германия являются центрами аннигиляции первичных радиационных дефектов.
Легирование кремния германием приводит к снижению эффективности образования А-центров и некоторому снижению эффективности образования дивакансий.
При низкотемпературном электронном облучении монокристаллов легированных германием возможно протекание квазихимических реакций:
е → I, V1 V2 (I + V) 1) V + V → V2 2) V2 + I → V2 I 3) V + O → V 4) Ge + V → GeV 5) GeV + I → Ge 6) V + O → A 7) A + I → O
Присутствие германия в решётке кремния сказывается на эффективность накопления А-центров и СОV2 (концентрация дефектов выше в образцах Si<Ge> по сравнению с контрольными образцами), тогда как скорость образования У-центров практически не зависит от содержания германия.
Это объясняется с учётом деформации сжатии и полей упругих напряжений при введении атомов германия, которые могут существенно влиять на миграцию дефектов и примесей.
В окрестностях атома Ge находится атом углерода в узле решётки либо углерод и кислород в кремнии образуют ассоциации СО, которые могут быть зародышами для образования комплексов СОV2.
Гетерируемые облучением собственные междоузельные атомы под воздействием создаваемых атомами германия деформационных полей выталкиваются из областей напряжения и захватываются расположенными вне их стоками. Вакансии, напротив, мигрируют к областям, где вступают во взаимодействие с находящимися там примесными атомами и их ассоциациями, образуя с ними стабильные комплексы. Небольшое увеличение эффективности образования А-центров связано с меньшей долей растворённого кислорода, находящегося в создаваемых германием областях напряжения, по сравнению с его содержанием в объёме кристалла.
При исследовании спектров ЭПР и ИК поглощения образцов Si<Ge> n-типа проводимости NGe ≈ 1 атомных процентов) облученных электронами с энергией 2,5 МэВ дозой Ф > 1016см-2 при Т = 300К были обнаружены А-центры и дивакансии. Их концентрация в несколько раз уменьшается при введении германия. Это свидетельствует о существенном влиянии германия а дефектообразования в кремнии, которое объясняется исходя из предположения: 1) введения германия в кремний приводит к образованию новых термически устойчивых радиационных дефектов, в состав которых входят вакансии; 2) германий способствует образованию центров непрямой аннигиляции.
Введение германия приводит к уменьшению центров непрямой аннигиляции.
Интерпретация результатов о влиянии германия в монокристаллах кремния на процессы образования и аннигиляции радиационных дефектов неоднородна. Одни учёные считают, что центрами аннигиляции первичных радиационных дефектов являются атомы германия, другие полагают, что такими центрами являются атомы кислорода.
Имеются разные данные о влиянии германия на процессы образования и отжига А-центров. Различные работы дают разный результат. В одних случаях скорость введения А-центров уменьшается, в других не изменяется, в третьих увеличивается их концентрация.
Таблица 5. Параметры дефектов, образующиеся в легированных германием монокристаллах кремния, подвергнутом облучению.
Неоднозначны представления учёных об образовании вторичных радиационных дефектах в монокристаллах кремния, содержащих германий. Одни считают, что введение германия приводит к образованию дефектов, в состав которых входят вакансии. Другие полагают, что германий способствует накоплению междоузельных атомов. Германий в монокристаллах кремния уменьшает концентрацию дефектов и вакансионного, и междоузельного типа.
Поведение P в Si
Рис. 4. Фазовые диаграммы Si-P Фосфор - примесь V группы, образует в германии и кремнии примесные центры, для которых применима теория эффективной массы. Замещая атом кремния в узле кристаллической решетки, примесный атом отдает четыре электрона из валентной (s+p)-оболочки на образование связей с окружающими атомами, а пятый валентный электрон оказывается «лишним».
Таблица 6. Энергия оптических переходов для доноров V группы в кремнии.
Примесный атом F является эффективным центром захвата свободных вакансий, в результате чего образуется комплекс вакансия – донор (Е-цент). Модель такого центра: один из узлов кристаллической решетки в ближайшем окружении примесного атома оказывается вакантными. Возможна другая конфигурация: комплекс, состоящий из донора и пары полувакансий, примесный атом в этом случае имеет шесть ближайщих соседей.
Е-центр обладает глубоким акцепторным состоянием вблизи середины запрещенной зоны. Для Е-центра возможны два типа переориентаций. Первый тип связан с переключением связей атомов в окрестности вакантного узла, при этом положение оси дефекта вакансия – донор в кристалле не изменяется. Такая переориентация характеризуется малыми величинами энергии активации, поскольку основной вклад в энергию вносит «электронный» процесс переключения связей. Второй тип связан в атомной перестройкой Е-центра, в результате которой положение оси дефекта изменяется, в этом случае энергия активации существенно больше.
В процессе переориентации вакансия совершает четыре диффузионных прыжка вокруг примесного атома. При этом, несмотря на частичное разъединение пары, энергия связи комплекса оказывается достаточной и диссоциации Е-центра не наблюдается. Хотя оценки энергии связи дефектов Есв в таком комплексе различны, тем не менее ясно, что в любом случае она не меньше энергии, требующейся для переориентации Е-центра.
Диффузию Е-центра можно представить как результат последовательного действия двух процессов: сначала происходит, например, переориентация дефекта, а затем примесный атом «прыгает» в вакантный узел и дефект перемещается в решетке на одно межатомное расстояние. Температура, при которой Е-центры в кремнии не стабильны (отжигаются), составляет ~ 140 °С и энергия активации зависит от тетраэдрического ковалентного радиуса r примесных атомов.
В сильнолегированном кремнии (с концентрацией примеси P больше 1017см-3) могут образоваться дефекты с включением двух (и более) примесных атомов, некоторые из этих центров по типу электрической активности является донорами. Нужно также отметить, что в кремнии возможны дефекты межузельного типа.
Процесс распределения примесей связаны с различной степенью их растворимости в жидкой и твердой фазах, т.е. зависят от равновесного коэффициента (k0) определяемого как отношения содержания примеси в твердой фазе и содержанию её в жидкой фазе. k0 = Ст/Сж Примеси с разными коэффициентами распределения по объему твердой фазы по разному.
Коэффициент распределения в свою очередь находится в определенной зависимости от условий процесса кристаллизации. При росте кристаллов в реальных условиях получаются эффективные значения коэффициента распределения примесей. Эффективный коэффициент распределения в первом приближении является функцией скорости роста кристалла и выражается уравнением Бартона-Прима-Слихтера. kэфф = k0/[k0-(1-k0)exp(-fδ/D)], где f – скорость роста, δ – толщина слоя расплава вблизи границы раздела фаз, в которой перенос примесей преимущественно осуществляется путём диффузии, D – коэффициент диффузии примеси в расплаве.
Такая зависимость распределения примеси в условиях роста кристаллов позволяет устанавливать требуемые условия для управления процессом распределения примесей посвещено немало работ, в том числе и коэффициенту распределения германия в кремнии kэфф = 0,33.
С повышением содержания Ge и при выбранных условиях выращивания увеличивается эффективный коэффициент распределения Ge в Si.
Метод Чохральского и метод получения монокисталлов вытягиванием из расплава не обеспечивает равномерности состава по длине легированного кристалла, следовательно, не обеспечивает однородности. В зависимости от значения коэффициента распределения этот градиент может быть разным. Коэффициент распределения германия в кремнии меньше единицы (k < 1), поэтому концентрация германия вблизи затравки минимальна и постоянно увеличивается к концу кристалла.
На основе метода Чохральского были разработаны более совершенные методы, обеспечивающие однородность кристаллизующейся твердой фазы. Одним из таких методов является метод жестко закрепленных сообщающихся сосудов, которые позволяет получать однородно легированные монокристаллы. Он относится к методам с жидкофазной капиллярной подпиткой позволяет выращивать не только однородно легированные, но и совершенные, в том числе бездислокационные, монокристаллы.
Рис. 5. Схема МЖЗСС.
Рабочий и подпитывающие объемы представляют собой цилиндрические, коаксиально расположенные сообщающиеся сосуды (тигли). Поступления подпитывающего расплава, осуществляется из внешнего тигля во внутренний через капиллярное отверстие и определяется только количеством затвердевшего вещества. Конструкция тиглей обеспечивает равенство потоков подпитывающего расплава (Uп), поступающего через капиллярное отверстие, и «потока кристаллизации» (Uкр) кристаллизующего расплава. Uп=Uкр Uкр = (π/4)Ǿкр2Vр, где Ǿкр2 – диаметр кристалла; Vр – скорость роста. Uп = (π/4)Ǿп2Vп, где Ǿп2 – диаметр капиллярного отверстия; Vп – скорость подпитки. ð Uп/Uр = Ǿкр2 / Ǿп2 .
Расплав во внутреннем тигле легировали германием. Во время процесса выращивания обеспечивали независимость составов в обоих тиглях. Диффузионный поток примеси (германия) из внутреннего тигля во внешний через капиллярный канал был подавлен, т.к Dж/lкан << Dп, где Dж – коэффициент диффузии примеси в жидкости, lкан – длина капиллярного канала (равна толщине стенки внутреннего кварцевого тигля).
Уравнение, связывающее геометрические размеры тиглей и концентрацию легирующией добавки в расплаве:
(S1 + S2)/S2 = (Cж1i – Сжпi)/(Cж1i – Cmi)
где S1 и S2 - площади поперечных сечений внутреннего и внешнего тиглей Cmi – концентрация i-й добавки в монокристалле; Cж1i – концентрация i-й добавки в рабочем V расплава; Сжпi – концентрация i-й добавки в подпитывающем V расплава.
МЖЗСС способствует получению структурно совершенных монокристаллов, так как расплав, находящийся во внешнем (по отношению к рабочему объёму расплава) тигля выполняет роль не только подпитывающего расплава, но и теплового экрана. Последнее способствует уменьшению осцилляций температуры в рабочем объёме расплава.
Расчет параметров процесса выращивания Геометрические размеры монокристалла:
Диаметр кристалл: D = 200 мм Длина кристалла: L = 1000 мм
Параметры технологического процесса:
Скорость роста: U = 1мм/мин Скорость вращения кристалла Vкр = 5 об/мин Скорость вращения тигля Vт = 8 об/мин
Расчеты:
1. Эффективные коэффициент распределения Ge в Si: kэфф = 0,6.
2. Рассчитываем динамическую вязкость расплава:
Коэффициент кинематической вязкости v = 3.48 107 м/с Плотность кремния r = 2.53 г/см3
3. Рассчитываем коэффициент взаимодиффузии:
ri=0.117
4. Рассчитываем угловую скорость вращения монокристалла:
5. Считаем глубину залегания p-n перехода (толщину диффузионного слоя).
6. Рассчитываем площадь поперечного сечения πr2 ~ 300 см2
7. Рассчитываем площадь поперечного сечений капиллярного отверстия.
Uкр = (1/600) см/сек Uп = 2 см/сек Ǿкр = 300 см2
Uкр = (π/4)Ǿкр2Vр, Uп = (π/4)Ǿп2Vп Uп/Uр = Ǿкр2 / Ǿп2
Ǿп = 8. Рассчитываем объем загрузки
V = DL = 30000 см3 M = Vr = 30000 ∙ 2.53 ~ 80 кг
Объём загрузки берётся с запасом, т.к часть расплава останется в тигле Mзагрузки = 90 кг.
Геометрические размеры тиглей:
Площадь поперечного сечения основного тигля: S1 = 350 см2 Площадь поперечного сечения подпитывающего тигля: S2
Рассчитаем площадь поперечного сечения подпитывающего тигля:
При таких параметрах удается вырастить монокристалл кремния с однородно распределенной примесью Ge.
Сопротивление материала:
Выращивание происходит в нейтральной среде газа Ar.
Рис. 6. Схема распределения gradT.
Основными управляемыми режимами термической обработки являются скорость нагрева и охлаждения, температура и продолжительность изотермической выдержки, среда нагрева и охлаждения. Выращенный кристалл подвергается отжигу и последующем медленном охлаждении. Цель отжига – это ликвидация химических и структурных неоднородностей, вызванных предшествующей обработкой. В ходе термообработки при 350˚С образцов Si<Ge,B> в течение 50 ч образовались низкотемпературные термодоноры. Механизмы роста позволяют получать монокристаллы практически любого элементарного полупроводника, соединения или твердого раствора свободными от ростовых неравновесных дефектов. Однако вблизи температуры кристаллизации растущий монокристалл содержит собственные точечные дефекты и атомы легирующих примесей.
Равновесные концентрации СТД, ТДФ и ТДЛ зависят от температуры. Поэтому при постростовом охлаждении монокристаллы, как правило, становятся пересыщенными твердыми растворами по СТД, ТДФ И ТДЛ, причем величина пересыщения по разным типам точечных дефектов может быть различной. В связи с этим в ходе постростового охлаждения и других видов термической обработки в монокристаллах могут проходить процессы распада пересыщенных твердых растворов. В большинстве случаев эти процессы приводят к образованию новых дефектов.
В зависимости от тепловых параметров охлаждающего после кристаллизации монокристалла в нем могут получаться преимущественное развитие процессы формирования тех или иных микродефектов. В. В. Воронковым введен критерий η, позволяющий оценить, какой из типов микродефектов будет образовываться преимущественно: η = Vн.р./gradTz, где Vн.р. – скорость роста монокристаллов, см∙с-1; gradTz – осевой градиент температур, К∙см-1.
В структуру критерий η заложены параметры, позволяющие оценить примерное время, в течение которого в бездислокационном монокристалле будут эффективно проходить диффузионные процессы, связанные с аннигиляцией и рекомбинацией СТД, концентрация которых превышает равновесную. Также этот критерий можно использовать и для оценки процессов образования микродефектов в монокристаллах других веществ.
Определена величина η = ηt, при которой микродефекты разных типов образуются в монокристалле в небольших и примерно равных концентрациях. Если в выращенном монокристалле η < ηt, то в нем образуются преимущественно микродефекты межузельного типа, если в выращенном монокристалле η > ηt, то в монокристалле образуются микродефекты вакансионного типа. При выращивании бездислокационных монокристаллов, изменяя параметры процесса роста (Vн.р., gradTz, уровень легирования), можно менять соотношение между микродефектами разными типов.
ηt = 3,3 ∙10-5 см2/сК η = Vн.р./gradTz = (1/600)/50 = 3,3∙10-5 см2/сК.
Расчет концентрации междоузельных дефектов и вакансий:
Т.е. при таких условиях роста монокристалла появление междоузельных и вакансионных микродефектов минимальна.
Концентрация германия намного больше концентрации легирующей примеси. В рассматриваемом материале концентрация германия 1020см-3, концентрация фосфора различна в начале и в конце кристалла 1 ∙1015 - 2,2∙1015 см-3. Время жизни неосновных носителей заряда τннз = 50 мкс. Концентрация примеси кислорода No = 6∙1017см-3. Удельное сопротивление материала ρ = 13 Ом∙см. Подвижность неосновных носителей заряда 480 см2/В∙с. Монокристалл бездислокационный.
Распад пересыщенного твердого раствора возможен до равновесной концентрации кислорода с образованием второй фазы SiO2.
Кинетика роста зародышей может лимитироваться либо скоростью присоединяющих атомов, либо скоростью подхода этих атомов из матрицы к зародышу, то есть их диффузией. Второй процесс идёт медленнее, чем первый, поэтому он и определяет кинетику распада твердого раствора.
Кинетика распада пересыщенного твердого раствора кислорода в кремнии описывают с помощью уравнения Хэма:
y = 1 – exp(-k∙tn), где y = [C0-Ct]/[ C0-Cα]; где C0 - исходная концентрация межузельного кислорода; Ct – концентрация кислорода в момент времени t; Cα – растворимость кислорода в твердой фазе; n – показатель степени, зависящей от механизма превращения.
Хэм установил: k = 3D(VC0)1/3F(2πNp/3)2/3
где Np – концентрация зародышей новой фазы; F – фактор зависящий от геометрической формы; D – коэффициент диффузии межузельного O2 в матрице; V – объём, приходящийся на атом примеси в выделяющейся фазе.
Использованнаялитература: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Метод МЖЗСС основан на том, что в процессе выращивания в расплаве, в районе фронта кристаллизации, поддерживается постоянная концентрация примеси и поддерживается постоянный коэффициент распределения примеси.
Метод МЖЗСС основан на том, что в процессе выращивания в расплаве, в районе фронта кристаллизации, поддерживается постоянная концентрация примеси и поддерживается постоянный коэффициент распределения примеси. =8,804 10-4 см2/с.
=8,804 10-4 см2/с. =5.14 10-5 см2/с
=5.14 10-5 см2/с = 2 ∙3,14∙/5 = 1,256 1/сек
= 2 ∙3,14∙/5 = 1,256 1/сек = 2.2 ∙ (3.48 109 )0.17 ∙ (5.14 10-5)0.33 ∙ 1,256-0.5 = 0,316 см.
= 2.2 ∙ (3.48 109 )0.17 ∙ (5.14 10-5)0.33 ∙ 1,256-0.5 = 0,316 см. =8,66 см2
=8,66 см2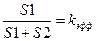

 Ом∙см
Ом∙см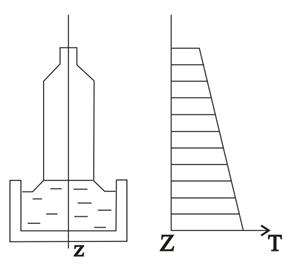 При выращивании монокристаллов удается достичь осевой градиент температур gradTр = 0. В нашем случае gradT ~ 50К/см.
При выращивании монокристаллов удается достичь осевой градиент температур gradTр = 0. В нашем случае gradT ~ 50К/см.
