Гиперболический параболоид
Поверхности вращения
Определение 82
Будем говорить, что поверхность второго порядка является поверхностью вращения в некоторой системе координат она задается уравнением 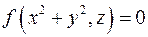 , где , где  является алгебраическим многочленом второго порядка относительно является алгебраическим многочленом второго порядка относительно 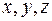 . Можно показать, что в этом случае уравнение имеет вид . Можно показать, что в этом случае уравнение имеет вид  . .
Замечание
Все эти поверхности получаются вращением кривой 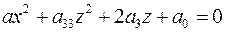 в плоскости в плоскости 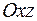 вокруг оси вокруг оси 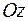 . Таким образом поверхность вращения полностью определяется кривой второго порядка в плоскости . Таким образом поверхность вращения полностью определяется кривой второго порядка в плоскости 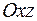 . .
Напишем канонические уравнения некоторых поверхностей вращения:
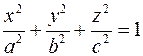 - эллипсоид - эллипсоид
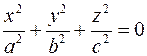 - вырожденный эллипсоид - вырожденный эллипсоид
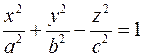 - однополостный гиперболоид - однополостный гиперболоид
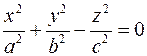 - конус - конус
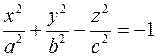 - двуполостный гиперболоид - двуполостный гиперболоид
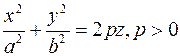 - параболоид - параболоид
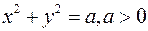 - цилиндр - цилиндр
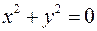 - вырожденный цилиндр - вырожденный цилиндр
Пусть есть поверхность второго порядка и плоскость. Рассмотрим их пересечения. Введем систему координат так, чтобы уравнение плоскости записывалось 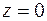 . Пусть в этой системе координат уравнение поверхности . Пусть в этой системе координат уравнение поверхности  В сечении плоскостью В сечении плоскостью 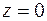 получаем получаем  . Если . Если 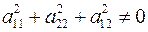 , то это кривая второго порядка. Если , то это кривая второго порядка. Если 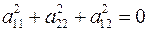 , то в сечении получается кривая , то в сечении получается кривая 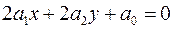 . При . При 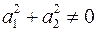 это прямая. При это прямая. При 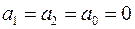 получаем плоскость получаем плоскость  . При . При 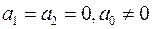 точек пересечения нету. Таким образом получаем, что плоскость может пересекать поверхность по кривой второго порядка, по прямой, по плоскости и может не иметь общих точек. Рассмотрим отдельно случай, когда плоскость пересекается поверхность второго порядка по плоскости. В выбранной ранее системе координат уравнение поверхности имеет вид точек пересечения нету. Таким образом получаем, что плоскость может пересекать поверхность по кривой второго порядка, по прямой, по плоскости и может не иметь общих точек. Рассмотрим отдельно случай, когда плоскость пересекается поверхность второго порядка по плоскости. В выбранной ранее системе координат уравнение поверхности имеет вид 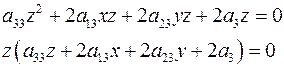
Эллипсоид сечении получается кривая Если ние поврехности к, чтобы уравнение плоскости записывалось ЭллЭЭлвЭлавв
Определение 83
Поверхность, записанная в некоторой системе координат уравнением 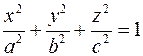 называется эллипсоидом. Это уравнение и система координат называются каноническими. Иногда требует, чтобы называется эллипсоидом. Это уравнение и система координат называются каноническими. Иногда требует, чтобы 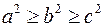

Свойства
1) Эллипсоид обладает единственным центром симметрии. Центром симметрии является точка  . .
2) Координатные плоскости являются плоскостями симметрии.
3) Координатные оси являются осями симметрии.
4) Эллипсоид является ограниченным телом. Он заключен в параллелепипед 
Сечение плоскостью  . При . При 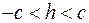 получаем в сечении эллипс получаем в сечении эллипс
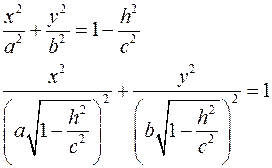
При 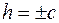 получаем вырожденный эллипс получаем вырожденный эллипс
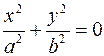
При 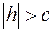 точек пересечения нет точек пересечения нет
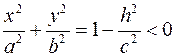
Аналогично рассматриваются сечения плоскостями 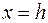 и и 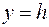 . .
Сечение произвольной плоскостью  . Будем считать без ограничения общности, что . Будем считать без ограничения общности, что 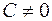 . .
 и в сечении получим кривую, проекция которой на плоскость и в сечении получим кривую, проекция которой на плоскость  описывается уравнением описывается уравнением
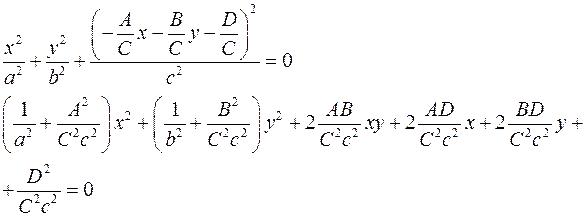
Вычислив инварианты, легко видеть, что это эллиптическое уравнение и возможны случаи, когда это эллипс, вырожденный эллипс и мнимый эллипс. Только у эллиптических кривых при проектировании на плоскость может получиться эллиптическая кривая.
Однополостный гиперболоид
Определение 84
Поверхность, задающаяся в некоторой декартовой системе координат уравнением 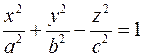 называется однополосным гиперболоидом. называется однополосным гиперболоидом.
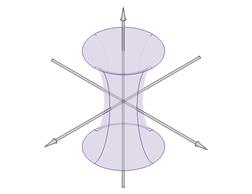
Свойства
1) Однополосный гиперболоид не является ограниченной поверхностью.
2) Начало координат является центром симметрии этой поверхности.
3) Координатные плоскости являются плоскостями симметрии поверхности.
Рассмотрим честь сечений поверхности.
1) Плоскость 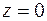 пересекает поверхность по эллипсу пересекает поверхность по эллипсу 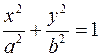 (это уравнение кривой второго порядка на плоскости, которая является проекцией эллипса на плоскость (это уравнение кривой второго порядка на плоскости, которая является проекцией эллипса на плоскость  ). ).
2) Плоскость  пересекает поверхность по кривой, проекция которой на плоскость записывается уравнением пересекает поверхность по кривой, проекция которой на плоскость записывается уравнением 
Плоскость  пересекает поверхность по гиперболе пересекает поверхность по гиперболе 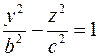 . .
Плоскость 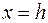 , где , где  пересекает поверхность по гиперболе, проекция которой на пересекает поверхность по гиперболе, проекция которой на 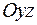 описывается уравнением описывается уравнением 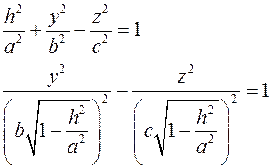
Плоскость 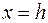 , где , где 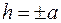 пересекает поверхность по кривой, проекция которой на плоскость пересекает поверхность по кривой, проекция которой на плоскость 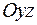 описывается уравнением описывается уравнением 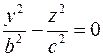 . Это уравнение двух пересекающихся прямых. Значит сечение является пересекающимися прямыми. Плоскость . Это уравнение двух пересекающихся прямых. Значит сечение является пересекающимися прямыми. Плоскость 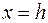 , ,  или или 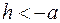 пересекает поверхность по гиперболе, уравнение проекции которой на плоскость пересекает поверхность по гиперболе, уравнение проекции которой на плоскость 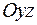 описывается уравнением описывается уравнением 
Аналогично для плоскости 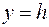 . .
Рассмотрим сечение плоскостью 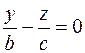 . Эта плоскость пересекает поверхность по кривым, проекции которых на плоскость . Эта плоскость пересекает поверхность по кривым, проекции которых на плоскость  описываются уравнениями описываются уравнениями 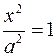 . Это пара параллельных прямых. Поэтому сечение тоже является парой параллельных прямых: . Это пара параллельных прямых. Поэтому сечение тоже является парой параллельных прямых: 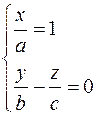 и и 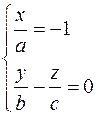 . .
Рассмотрим сечение плоскостью  . Эта плоскость пересекает поверхность по кривой, проекция которой на плоскость описывается уравнением . Эта плоскость пересекает поверхность по кривой, проекция которой на плоскость описывается уравнением 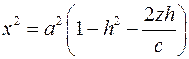 . Это парабола. . Это парабола.
В сечении может получиться эллипс, гипербола, пара пересекающихся прямых, пара параллельных прямых и парабола.
Двуполостный гиперболоид
Определение 85
Поверхность, которая в некоторой декартовой системе координат задается уравнением 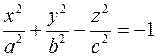 называется двуполостным гиперболоидом. называется двуполостным гиперболоидом.
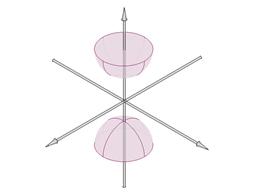
Свойства
1) Однополосный гиперболоид не является ограниченной поверхностью.
2) Начало координат является центром симметрии этой поверхности.
3) Координатные плоскости являются плоскостями симметрии поверхности.
4) Так как сечение плоскости 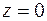 не содержит ни одной точки, то поверхность распадается на две части. не содержит ни одной точки, то поверхность распадается на две части.
Рассмотрим некоторые сечения.
Плоскость 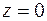 . В сечении получается кривая второго порядка, задаваемая уравнением . В сечении получается кривая второго порядка, задаваемая уравнением  . Этому уравнению не удовлетворяет ни одна точка плоскости . Этому уравнению не удовлетворяет ни одна точка плоскости  , значит сечение не содержит ни одной точки. Аналогично сечение поверхности плоскостью , значит сечение не содержит ни одной точки. Аналогично сечение поверхности плоскостью 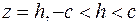 не содержит ни одной точки. не содержит ни одной точки.
Пересечением с плоскостью  , где , где 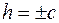 является вырожденный эллипс является вырожденный эллипс 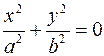 . .
Пересечением с плоскостью  является эллипс, проекция которого на плоскость является эллипс, проекция которого на плоскость  описывается уравнением описывается уравнением 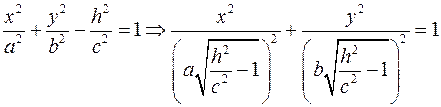 . .
Пересечением поверхности плоскостью  является гипербола, проекция которой на плоскость является гипербола, проекция которой на плоскость 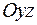 описывается уравнением описывается уравнением 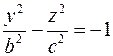 . Пересечением поверхности плоскостью . Пересечением поверхности плоскостью 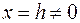 является гипербола, проекция которой на плоскость является гипербола, проекция которой на плоскость 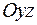 описывается уравнением описывается уравнением 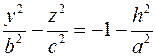 или или 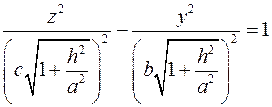 . .
Легко видеть, что плоскость 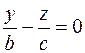 не имеет общих точек с поверхностью. не имеет общих точек с поверхностью.
Плоскость  пересекает поверхность по кривой, проекция которой описывается уравнением пересекает поверхность по кривой, проекция которой описывается уравнением 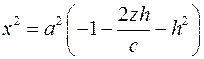 . Это парабола. . Это парабола.
Эллиптический параболоид
Определение 86
Поверхность, которая в некоторой декартовой системе координат задается уравнением 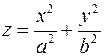 называется эллиптическим параболоидом. называется эллиптическим параболоидом.
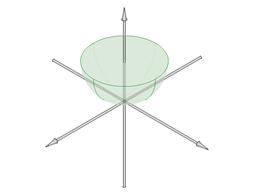
Свойства
1) Поверхность не является ограниченной.
2) Поверхность не имеет центров симметрии.
3) Поверхностей симметрична относительно плоскостей 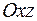 и и 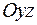 . .
Рассмотрим часть сечений поверхности плоскостями.
Плоскость 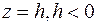 не имеет общих точек с поверхностью. Плоскость не имеет общих точек с поверхностью. Плоскость 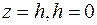 пересекает поверхность в одной точке, описываемой в плоскости пересекает поверхность в одной точке, описываемой в плоскости 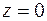 уравнением уравнением 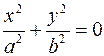 . Плоскость . Плоскость 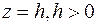 пересекает поверхность по кривой, проекция которой на плоскость пересекает поверхность по кривой, проекция которой на плоскость  описывается уравнением описывается уравнением  . Проекцией является эллипс, значит и в самом сечении эллипс. . Проекцией является эллипс, значит и в самом сечении эллипс.
Плоскость 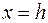 пересекает поверхность по параболе, проекция которой на плоскость пересекает поверхность по параболе, проекция которой на плоскость 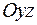 в плоскости в плоскости 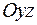 описывается уравнением описывается уравнением  . Аналогично для плоскости . Аналогично для плоскости 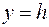 . .
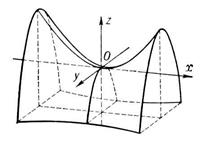
Гиперболический параболоид
Определение 87
Поверхность, которая в некоторой декартовой системе координат задается уравнением  называется гиперболическим параболоидом. называется гиперболическим параболоидом.
Свойства
1) Поверхность не является ограниченной.
2) Данная поверхность не имеет центра симметрии.
3) Данная поверхность симметрична относительно координатных плоскостей 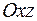 и и 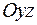 . .
Рассмотрим часть сечений поверхности плоскостями.
Плоскость 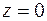 пересекает поверхность по паре пересекающихся прямых пересекает поверхность по паре пересекающихся прямых 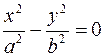 (уравнение в плоскости (уравнение в плоскости  ). Плоскость ). Плоскость 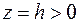 пересекает поверхность по гиперболе, проекция которой на плоскость пересекает поверхность по гиперболе, проекция которой на плоскость  в плоскости в плоскости  описывается уравнением описывается уравнением 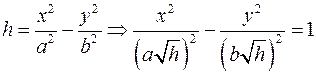 . Плоскость . Плоскость  пересекает поверхность по гиперболе, проекция которой на плоскость пересекает поверхность по гиперболе, проекция которой на плоскость  в плоскости в плоскости  описывается уравнением описывается уравнением 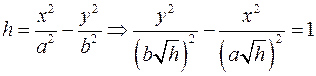 . .
Плоскость 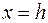 пересекает поверхность по параболе, проекция которой на плоскость пересекает поверхность по параболе, проекция которой на плоскость 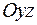 в плоскости в плоскости 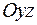 описывается уравнением описывается уравнением  . Это одинаковые параболы, полученные друг из друга параллельным переносом. . Это одинаковые параболы, полученные друг из друга параллельным переносом.
В сечение плоскостью 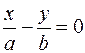 получается плоскость получается плоскость 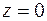 . Это плоскость . Это плоскость  . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


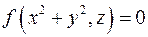 , где
, где  является алгебраическим многочленом второго порядка относительно
является алгебраическим многочленом второго порядка относительно 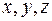 . Можно показать, что в этом случае уравнение имеет вид
. Можно показать, что в этом случае уравнение имеет вид  .
.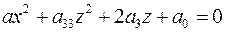 в плоскости
в плоскости 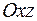 вокруг оси
вокруг оси 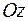 . Таким образом поверхность вращения полностью определяется кривой второго порядка в плоскости
. Таким образом поверхность вращения полностью определяется кривой второго порядка в плоскости 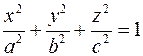 - эллипсоид
- эллипсоид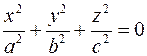 - вырожденный эллипсоид
- вырожденный эллипсоид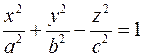 - однополостный гиперболоид
- однополостный гиперболоид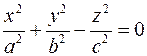 - конус
- конус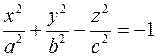 - двуполостный гиперболоид
- двуполостный гиперболоид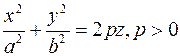 - параболоид
- параболоид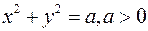 - цилиндр
- цилиндр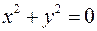 - вырожденный цилиндр
- вырожденный цилиндр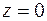 . Пусть в этой системе координат уравнение поверхности
. Пусть в этой системе координат уравнение поверхности  В сечении плоскостью
В сечении плоскостью  . Если
. Если 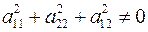 , то это кривая второго порядка. Если
, то это кривая второго порядка. Если 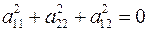 , то в сечении получается кривая
, то в сечении получается кривая 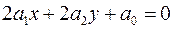 . При
. При 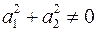 это прямая. При
это прямая. При 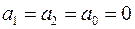 получаем плоскость
получаем плоскость  . При
. При 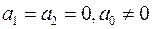 точек пересечения нету. Таким образом получаем, что плоскость может пересекать поверхность по кривой второго порядка, по прямой, по плоскости и может не иметь общих точек. Рассмотрим отдельно случай, когда плоскость пересекается поверхность второго порядка по плоскости. В выбранной ранее системе координат уравнение поверхности имеет вид
точек пересечения нету. Таким образом получаем, что плоскость может пересекать поверхность по кривой второго порядка, по прямой, по плоскости и может не иметь общих точек. Рассмотрим отдельно случай, когда плоскость пересекается поверхность второго порядка по плоскости. В выбранной ранее системе координат уравнение поверхности имеет вид 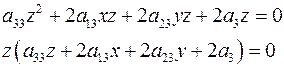
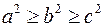

 .
.
 . При
. При 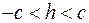 получаем в сечении эллипс
получаем в сечении эллипс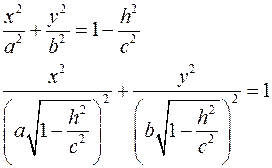
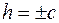 получаем вырожденный эллипс
получаем вырожденный эллипс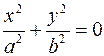
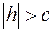 точек пересечения нет
точек пересечения нет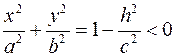
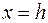 и
и 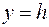 .
. . Будем считать без ограничения общности, что
. Будем считать без ограничения общности, что 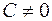 .
. и в сечении получим кривую, проекция которой на плоскость
и в сечении получим кривую, проекция которой на плоскость 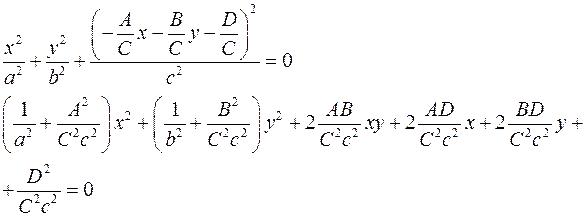

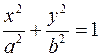 (это уравнение кривой второго порядка на плоскости, которая является проекцией эллипса на плоскость
(это уравнение кривой второго порядка на плоскости, которая является проекцией эллипса на плоскость 
 пересекает поверхность по гиперболе
пересекает поверхность по гиперболе 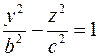 .
. пересекает поверхность по гиперболе, проекция которой на
пересекает поверхность по гиперболе, проекция которой на 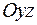 описывается уравнением
описывается уравнением 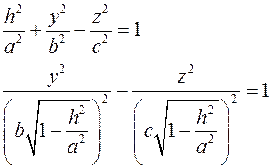
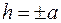 пересекает поверхность по кривой, проекция которой на плоскость
пересекает поверхность по кривой, проекция которой на плоскость 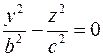 . Это уравнение двух пересекающихся прямых. Значит сечение является пересекающимися прямыми. Плоскость
. Это уравнение двух пересекающихся прямых. Значит сечение является пересекающимися прямыми. Плоскость  или
или 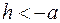 пересекает поверхность по гиперболе, уравнение проекции которой на плоскость
пересекает поверхность по гиперболе, уравнение проекции которой на плоскость 
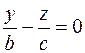 . Эта плоскость пересекает поверхность по кривым, проекции которых на плоскость
. Эта плоскость пересекает поверхность по кривым, проекции которых на плоскость 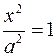 . Это пара параллельных прямых. Поэтому сечение тоже является парой параллельных прямых:
. Это пара параллельных прямых. Поэтому сечение тоже является парой параллельных прямых: 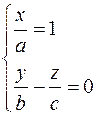 и
и 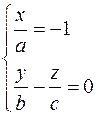 .
. . Эта плоскость пересекает поверхность по кривой, проекция которой на плоскость описывается уравнением
. Эта плоскость пересекает поверхность по кривой, проекция которой на плоскость описывается уравнением 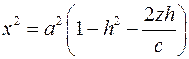 . Это парабола.
. Это парабола.
 . Этому уравнению не удовлетворяет ни одна точка плоскости
. Этому уравнению не удовлетворяет ни одна точка плоскости 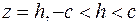 не содержит ни одной точки.
не содержит ни одной точки. является эллипс, проекция которого на плоскость
является эллипс, проекция которого на плоскость 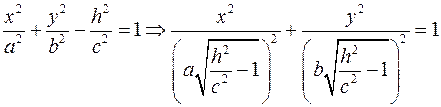 .
.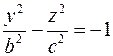 . Пересечением поверхности плоскостью
. Пересечением поверхности плоскостью 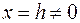 является гипербола, проекция которой на плоскость
является гипербола, проекция которой на плоскость 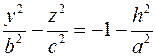 или
или 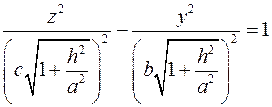 .
.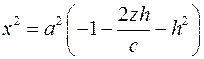 . Это парабола.
. Это парабола.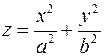 называется эллиптическим параболоидом.
называется эллиптическим параболоидом.
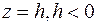 не имеет общих точек с поверхностью. Плоскость
не имеет общих точек с поверхностью. Плоскость 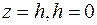 пересекает поверхность в одной точке, описываемой в плоскости
пересекает поверхность в одной точке, описываемой в плоскости 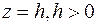 пересекает поверхность по кривой, проекция которой на плоскость
пересекает поверхность по кривой, проекция которой на плоскость  . Проекцией является эллипс, значит и в самом сечении эллипс.
. Проекцией является эллипс, значит и в самом сечении эллипс. . Аналогично для плоскости
. Аналогично для плоскости  называется гиперболическим параболоидом.
называется гиперболическим параболоидом.
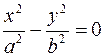 (уравнение в плоскости
(уравнение в плоскости 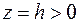 пересекает поверхность по гиперболе, проекция которой на плоскость
пересекает поверхность по гиперболе, проекция которой на плоскость 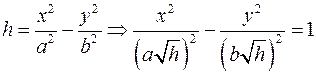 . Плоскость
. Плоскость  пересекает поверхность по гиперболе, проекция которой на плоскость
пересекает поверхность по гиперболе, проекция которой на плоскость 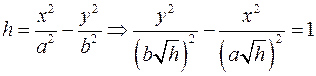 .
. . Это одинаковые параболы, полученные друг из друга параллельным переносом.
. Это одинаковые параболы, полученные друг из друга параллельным переносом.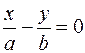 получается плоскость
получается плоскость