
|
|
Порядок выполнения работы и методические указания3.1 Косвенные измерения силы тока в электрической цепи. Схема эксперимента приведена на рис. 1 На рисунке 1 приняты следующие обозначения: Rн – сопротивление нагрузки источника напряжения; Rо –сопротивление измерительной катушки сопротивления или сопротивление младшей декады магазина сопротивлений.
Рисунок 1 Схема эксперимента для косвенного измерения силы тока в электрической цепи
В качестве Rн используется последовательное соединение сопротивлений R1 и R2 модуля, схема которого приведена на рисунке 2.
Рисунок 2 Схема модуля, используемого в качестве нагрузки
В приложении 2 для каждого модуля приведены номинальные значения сопротивлений резисторов R1 и R2 и пределы допускаемых отклонений сопротивлений от номинальных значений (погрешности изготовления). Так как сопротивление R0 включается в разрыв цепи и, следовательно, общее сопротивление цепи при этом изменяется, то необходимо выполнить условие:
Так, например, при Rн=1 кОм, Е=10 В сила тока в цепи составит 10 мА. Если выбрать Rо=1 Ом, то погрешность в определении тока в цепи из-за включения Rо составит
Для заданного модуля подсчитайте приблизительное значение тока в измерительной цепи:
и определите предел Uк измерений вольтметра. Если
Установите предел измерений Uк вольтметра ближайший больший рассчитанного значения Ux. В приведенном примере следует выбрать Uк =10 мВ (для прибора Щ300). Соберите схему эксперимента согласно рисунку 1 и произведите измерение падения напряжения на эталонном сопротивлении:
На основании показаний вольтметра и известного значения сопротивления Ro определите ток в цепи по закону Ома:
Пределы допускаемой относительной погрешности измерения тока
где
Погрешность – погрешности вольтметра – погрешности согласования (взаимодействия) При использовании прибора Щ300 на пределе 10 мВ пределы допускаемой относительной погрешности составляют:
где Тогда при
Погрешность согласования при измерении напряжения определяется выражением:
где Rвых – выходное сопротивление измерительной цепи относительно входных зажимов вольтметра; RV – внутреннее сопротивление вольтметра. Если в цепи на рис. 1 Rо = 1 Ом, то Сопротивление RV вольтметра Щ300 на пределе 10 мВ составляет 10 МОм. Тогда погрешность согласования составит:
что значительно меньше погрешности вольтметра Если
Сравнение Для исключения погрешности согласования
В рассматриваемом примере Iиспр = 7, 007 мА. В абсолютной форме погрешность результата измерений тока в цепи (округление значения погрешности проводим до двух значащих цифр):
Результат измерения силы тока в цепи:
Применение формулы (3) для суммирования двух значительно отличающихся составляющих погрешности нецелесообразно, так как будет получено завышенное значение по сравнению с предельным, полученным по формуле (2).
3.2 Косвенное измерение мощности, отдаваемой источником электрической энергии в нагрузку Схемы эксперимента для косвенного измерения мощности приведены на рис. 3а и 3б.
Рисунок 3 Схемы эксперимента для косвенного измерения мощности
На рис. 3а приняты следующие обозначения: А – амперметр с внутренним сопротивлением RА (комбинированный аналоговый прибор), измеряющий силу тока, потребляемого от источника напряжения; V – вольтметр цифровой с внутренним сопротивлением RV; Rн – сопротивление одного из резисторов модуля. Оценка мощности
Так как средства измерений всегда потребляют энергию от объекта измерений, то в схемах на рис. 3а и 3б наряду с инструментальными погрешностями следует учитывать и погрешность согласования (взаимодействия). Действительное значение мощности, отдаваемой источником в нагрузку (при условии, что приборы не потребляют энергии от источника):
где E ‑ действительное значение напряжения на зажимах источника напряжения (равное э.д.с. источника при условии равенства нулю его внутреннего сопротивления), I ‑ действительное значение силы тока через нагрузку.
Для схемы на рис. 3а
где RA – внутреннее сопротивление амперметра, определяемое по описанию прибора либо (для аналоговых комбинированных приборов) по формуле
где Iк – предел измерений; Uзаж – максимальное падение напряжения на зажимах прибора для выбранного предела измерений. Действительное значение силы тока:
где
RV – внутреннее сопротивление вольтметра, определяемое по описанию прибора либо (для аналоговых комбинированных приборов) по формуле
где Iпо – ток полного отклонения вольтметра для выбранного предела измерений. Действительное значение мощности, отдаваемой источником в нагрузку:
Для схемы на рис. 3б:
Значения RA, RV, Iпо и Uзаж определяют по пределам измерений используемых приборов (Приложения 3 - 6). Предел допускаемой относительной погрешности измерения мощности:
где Предел абсолютной погрешности определяют по формуле:
Результат измерения записывают в виде:
Абсолютная погрешность согласования при измерении мощности:
Рассчитайте значения погрешностей согласования при измерении мощности по схемам на рис. 3а и 3б и сравните их между собой.
3.3 Косвенное измерение емкости Косвенное измерение емкости основано на том, что для идеальных конденсаторов модуль импеданса равен реактивному сопротивлению
где f – частота питающего напряжения. По результатам прямых измерений среднеквадратических значений тока и напряжения модуль Z импеданса находим по формуле
Оценка
Пределы абсолютной и относительной погрешности косвенных измерений емкости определяют по следующим формулам:
где
где ΔU, ΔI и δU,δI – пределы абсолютных и относительных погрешностей измерений напряжения и тока, определяемые исходя из классов точности измерительных приборов (см. Приложения 7-8); Δf и δf – пределы абсолютной и относительной погрешности установки частоты генератора. Схема косвенного измерения емкости приведена на рисунке 4. На рисунке 4 приняты следующие обозначения: R – сопротивление, ограничивающее ток в цепи; Cx – измеряемая емкость конденсатора; A и V – амперметр и вольтметр с внутренними импедансами ZА и ZV. Схема подключается к генератору синусоидальных сигналов. При идеальном с точки зрения потребляемой мощности вольтметре (бесконечное внутреннее сопротивление
Рисунок 4 Схема для косвенного измерения емкости
Реальный вольтметр потребляет мощность, (т.е. имеет конечное внутреннее сопротивление), в результате чего амперметр измеряет ток через эквивалентное сопротивление Zэ параллельного соединения Zx и ZV, определяемое по формуле:
Модуль импеданса вольтметра:
где RV и CV ‑ входное сопротивление и входная емкость вольтметра (соединены параллельно). Оценка модуля импеданса объекта:
С учетом параллельного соединения Cx, RV и CV модуль эквивалентного сопротивления определяется по формуле
где Cэ = Cx + CV. Из данного выражения находят (вывод см. в Приложении 9)
Действительное значение измеряемой емкости:
Абсолютная и относительная погрешности согласования рассчитывается по формулам:
Таким образом, при измерении емкости погрешность согласования отрицательная и не зависит от R и Для проведения измерений в данной лабораторной работе установите частоту генератора 1 кГц, а выходное напряжение Uг около 10 В. По номинальному значению емкости конденсатора Cном (см. Приложение 2) следует рассчитать ожидаемое значение тока I в цепи и выбрать соответствующий предел измерений амперметра (ближайшее большее или равное ожидаемому значение):
Если Xc окажется больше 600 Ом, то дополнительное токоограничивающее сопротивление не требуется, в противном случае Выполнив измерения напряжения и силы тока, рассчитывают Cx. Погрешность измерения с учетом трех составляющих:
Результат измерения записывают в виде:
3.4 Косвенное измерение коэффициента деления делителя Делитель напряжения в данной работе представлен в виде резистивного модуля (см. рисунок 2). Измерение коэффициента деления Kд проводится по схеме на рисунке 5.
Рисунок 5 Схема для измерения коэффициента деления делителя
Для измерения Kд последовательно с помощью вольтметра проводят измерения напряжения на входе Uвх и на выходе Uвых делителя. Коэффициент деления определяется соотношением:
В качестве вольтметра используется многопредельный аналоговый комбинированный прибор. Для выполнения измерений установите напряжение источника равным 15 В. По номинальным сопротивлениям резисторов (см. Приложение 2) рассчитайте ожидаемое значение напряжения на выходе:
Произвести измерения Uвх и Uвых, обращая внимание на то, чтобы предел измерений вольтметра соответствовал значениям Uвх и Uвых. При измерении Uвых появляется погрешность согласования:
где
По показанию вольтметра и рассчитанному значению погрешности согласования определяется исправленное значение выходного напряжения:
Далее вычисляется оценка коэффициента деления
Погрешности
Предельная абсолютная погрешность измерения Kд рассчитывается по формуле:
Результат измерения записывают в виде:
На практике принято погрешность измерения коэффициента деления выражать в относительной форме.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.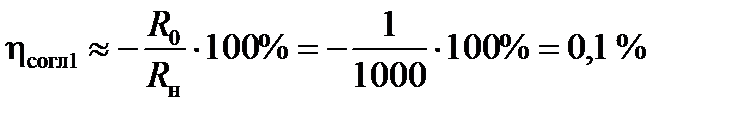 .
.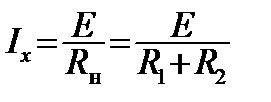
 и Rо=1 Ом, то падение напряжения на Rо:
и Rо=1 Ом, то падение напряжения на Rо: ; Uк=7 мА·1 Ом=7 мВ.
; Uк=7 мА·1 Ом=7 мВ. .
. .
. определяются следующим выражением:
определяются следующим выражением: ,
, – относительная погрешность измерения напряжения;
– относительная погрешность измерения напряжения; – погрешность сопротивления.
– погрешность сопротивления. , определяемой классом точности;
, определяемой классом точности; из-за влияния внутреннего сопротивления вольтметра.
из-за влияния внутреннего сопротивления вольтметра. , %,
, %, – показание вольтметра.
– показание вольтметра.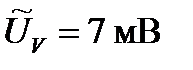
 .
.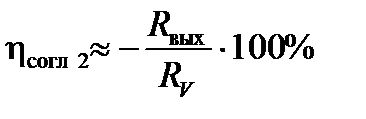 ,
, .
. ,
, можно пренебречь.
можно пренебречь. и
и  , то погрешность измерения силы тока не превысит:
, то погрешность измерения силы тока не превысит: .
. с погрешностью согласования
с погрешностью согласования  от включения в цепь сопротивления Rо, равной 0,1%, не позволяет пренебречь последней.
от включения в цепь сопротивления Rо, равной 0,1%, не позволяет пренебречь последней.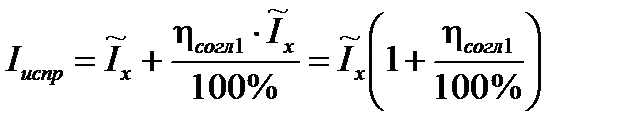 .
. ;
;  .
. .
. , отдаваемой источником электрической энергии в нагрузку Rн, рассчитывается по измеренным значениям
, отдаваемой источником электрической энергии в нагрузку Rн, рассчитывается по измеренным значениям  и
и  :
: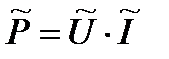 .
. ,
, ,
, ‑ падение напряжения на амперметре;
‑ падение напряжения на амперметре;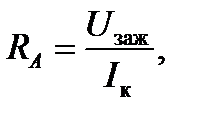
 ,
, ‑ исправленное значение силы тока в нагрузке (с учетом влияния внутреннего сопротивления амперметра);
‑ исправленное значение силы тока в нагрузке (с учетом влияния внутреннего сопротивления амперметра); ‑ сила тока через вольтметр;
‑ сила тока через вольтметр; ,
,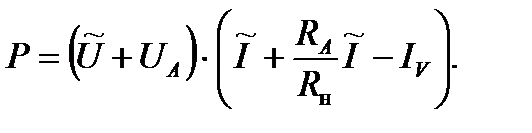
 ;
; ;
; .
. ,
, и
и  ‑ предельные относительные погрешности средств измерений, рассчитываемые по классам точности приборов (см. лабораторную работу Л-02-1).
‑ предельные относительные погрешности средств измерений, рассчитываемые по классам точности приборов (см. лабораторную работу Л-02-1). .
. .
.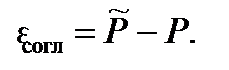
 (4)
(4)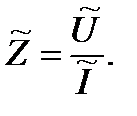
 при заданной частоте определяется выражением
при заданной частоте определяется выражением . (5)
. (5) ,
, ,
,  и
и  – частные производные функции (5) по аргументам U, I и f;
– частные производные функции (5) по аргументам U, I и f; , (6)
, (6) , (7)
, (7) ) в схеме на рисунке 4 оценка модуля импеданса объекта (конденсатора) не зависит от значений R, ZА и ZV.
) в схеме на рисунке 4 оценка модуля импеданса объекта (конденсатора) не зависит от значений R, ZА и ZV. .
.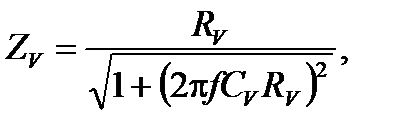
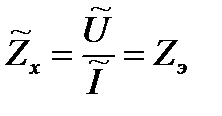 .
. ,
, .
. .
. .
. .
. . С увеличением частоты погрешность согласования уменьшается.
. С увеличением частоты погрешность согласования уменьшается. .
. (выставляется на магазине сопротивлений).
(выставляется на магазине сопротивлений). при
при  ;
; .
. ;
;  .
. .
. .
. ,
, ;
; и
и  – соответственно показание вольтметра и его входное сопротивление.
– соответственно показание вольтметра и его входное сопротивление. .
. и определяется погрешность его измерения по формуле:
и определяется погрешность его измерения по формуле: .
. и
и  рассчитывают по классу точности используемого вольтметра:
рассчитывают по классу точности используемого вольтметра: , (%).
, (%). .
.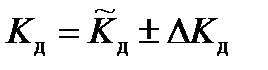 .
.