
|
|
Кратчайшие пути от фиксированной вершиныНАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ Начальные понятия Рассмотрим ориентированные графы Если в произвольном графе принять вес каждой дуги равным 1, то получается обычное определение длины пути как числа дуг. В случае веса, отличного от1, рассмотрим нахождение кратчайшего пути между фиксированными вершинами Практические интерпретации задачи о кратчайших путях могут быть следующими. Например, вершины соответствуют городам, а каждая дуга – некоторому пути, длина которого представлена весом дуги. Отыскиваются кратчайшие пути между городами. Вес дуги может соответствовать стоимости (или времени) передачи информации между вершинами. В таком случае ищется самый дешевый (самый быстрый) путь передачи информации. Будут рассмотрены алгоритмы нахождения расстояния между вершинами, а не самих путей. Но, зная расстояния, можно при условии положительной длины всех контуров, легко определить кратчайшие пути. Для этого отметим, что для произвольных Действительно, таким свойством обладает предпоследняя вершина произвольного кратчайшего пути из s в t. Далее находим вершину u, для которой d(s,v) = d(s,u) + a(u,v), и т. д. Из положительности длины всех контуров легко следует, что созданная таким образом последовательность t, v, u, . . . не содержит повторений и оканчивается вершиной s. Очевидно, что она определяет (при обращении очередности) кратчайший путь из s в t. Таким образом получается следующий алгоритм нахождения кратчайшего пути из s в t при известных расстояниях от фиксированной вершины s до всех остальных вершин v ориентированного графа G. Эти расстояния представлены в массиве D. Кольцевые структуры графа G содержат помимо номеров вершин (n), из которых приходят направленные дуги, также веса дуг (a), что будет отражено в операции circ.element.
Рис.2.1.Процедура нахождения кратчайшего пути в ориентированном графе.
Для всех последующих алгоритмов будем полагать, что
Кратчайшие пути от фиксированной вершины Большинство известных алгоритмов нахождения расстояния между двумя фиксированными вершинами s и t опирается на действия, которые в общих чертах можно представить следующим образом: при данной матрице весов дуг
D[u] + A[u,v] < D[v] (2.1)
оценку D[v] улучшают: D[v] = D[u] + A[u,v]. Процесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Легко показать, что значение каждой из переменных D[v] равно тогда d(s,v) – расстоянию от s до v. Для определения расстояния от s до t вычисляются расстояния от s до всех вершин графа. Не известен ни один алгоритм нахождения расстояния между двумя фиксированными вершинами, который был бы существенным образом более эффективен, нежели известные алгоритмы определения расстояния от фиксированной вершины до всех остальных. Описанная общая схема является неполной, так как она не определяет очередности, в которой выбираются вершины u и v для проверки условия (2.1). Эта очередность оказывает сильное влияние на эффективность алгоритма. Рассмотрим более детально методы нахождения расстояния от фиксированной вершины, называемой источником, всегда обозначаемого через s, до всех остальных вершин графа. Рассмотрим сначала алгоритм для общего случая, в котором предполагается только отсутствие контуров с отрицательной длиной. Ориентированный граф G в своих кольцевых структурах так же как в 2.1 содержит номера вершин (n) и веса дуг (a). В отличие от 2.1 номера вершин связаны не с приходящими дугами, а с выходящими.
Рис.2.2.Процедура нахождения расстояния от источника до всех вершин ориентированного графа – метод Форда-Беллмана.
Работа алгоритма Форда-Беллмана проиллюстрирована на рис.2.3, веса дуг даны числами в скобках.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , дугам которых приписаны веса. Это означает, что каждой дуге
, дугам которых приписаны веса. Это означает, что каждой дуге  поставлено в соответствие некоторое вещественное число
поставлено в соответствие некоторое вещественное число  , называемое весом данной дуги. Полагаем, кроме того, что отсутствующие дуги графа будут иметь бесконечно большие веса. Если последовательность вершин v0, v1, v2, . . . , vp определяет путь в G, то его длина определяется как сумма
, называемое весом данной дуги. Полагаем, кроме того, что отсутствующие дуги графа будут иметь бесконечно большие веса. Если последовательность вершин v0, v1, v2, . . . , vp определяет путь в G, то его длина определяется как сумма  .
. . Длину такого кратчайшего пути обозначим d(s,t) и назовем расстоянием от s до t (может быть и отрицательным). Если не существует ни одного пути из s в t, то
. Длину такого кратчайшего пути обозначим d(s,t) и назовем расстоянием от s до t (может быть и отрицательным). Если не существует ни одного пути из s в t, то  .
. существует вершина v, такая что d(s,t) = d(s,v) + a(v,t).
существует вершина v, такая что d(s,t) = d(s,v) + a(v,t). . Веса дуг будут либо содержаться в кольцевых структурах графа, либо в массиве
. Веса дуг будут либо содержаться в кольцевых структурах графа, либо в массиве  .
.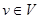 . Каждый раз, когда устанавливается, что
. Каждый раз, когда устанавливается, что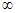 ; D[s] = 0
2. c = graph.fetch(G,s); i = circ.size(c)
3. пока i > 0
3.1. D[circ.element(c).n] = circ.element(c).a
3.2. circ.change(c); i = i – 1
4. для k = 1 до n-2
4.1. для v = 1 до n
4.1.1. если v < > s, то
4.1.1.1. для u = 1 до n
4.1.1.1.1. c = graph.fetch(G,u)
4.1.1.1.2. для i = 1 до circ.size(c) если (circ.element(c).n < > v), то circ.change(c)
иначе
4.1.1.1.2.1. a = circ.element(c).a + D[u]
4.1.1.1.2.2. если (a < D[v]), то D[v] = a
; D[s] = 0
2. c = graph.fetch(G,s); i = circ.size(c)
3. пока i > 0
3.1. D[circ.element(c).n] = circ.element(c).a
3.2. circ.change(c); i = i – 1
4. для k = 1 до n-2
4.1. для v = 1 до n
4.1.1. если v < > s, то
4.1.1.1. для u = 1 до n
4.1.1.1.1. c = graph.fetch(G,u)
4.1.1.1.2. для i = 1 до circ.size(c) если (circ.element(c).n < > v), то circ.change(c)
иначе
4.1.1.1.2.1. a = circ.element(c).a + D[u]
4.1.1.1.2.2. если (a < D[v]), то D[v] = a
