
|
|
Параметрические уравнения линий12 Цели Знать: v Основные способы преобразования прямоугольных координат; v уравнение кривых второго порядка с осями симметрии, параллельными координатным осям. Уметь: v переходить от одной прямоугольной системы координат к другой; v строить параллельно-смещённую кривую второго порядка по её уравнению.
Уравнения смещённых кривых второго порядка имеет вид:
где (х0; у0) — координаты центра кривой. Уравнения смещённой параболы:
где (х0;у0) — координаты вершины параболы.
Теорема. Уравнение вида всегда определяет:
При этом возможны случаи вырождения:
Пусть относительно системы декартовых прямоугольных координат на плоскости задана некоторая линия. Эту линию можно рассматривать как траекторию пути, пройденного точкой, движущейся по какому-нибудь закону. Если абсцисса точки М(х; у) изменяется по закону x=x(t), а ордината — по закону y=y(t),где t — параметр, то уравнение линии записывается в виде:
Эти уравнения называются параметрическими уравнениями линии. Составить уравнение линии на плоскости в выбранной системе координат — это, значит, составить такое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, которые на этой линии не лежат.
Постановка задачи:Составить уравнение линии на плоскости. План решения:1. Выбрать на плоскости систему координат; 2. на линии, уравнение которой выводится, взять произвольную точку с координатами (х; у). Основываясь на заданном свойстве всех точек, лежащих на линии, составить уравнение, связывающее координаты произвольной точки с некоторыми постоянными величинами, данными в задаче. Найденное уравнение и будет искомым.
№13. Даны точка А(1; 0) и прямая х=2. В декартовых координатах составить уравнение линии, каждая точка М(х; у) которой: 1) в два раза ближе к точке А, чем к данной прямой; 2) в два раза дальше от точки А, чем от заданной прямой; 3) равноудалена от точки А и от прямой х=2. ► 1) Пусть М — точка искомой линии (рис 13).
рис.13
По условию 2МА=МN.Отсюда, так как N(2; y), то
4х2 – 8х+4+4у2=х2 – 4х+4; 3х2 – 4х+4у2=0;
домножим на
2) По условию МА=2МN. Отсюда, так как N(2; y), то
х2 – 2х+1+у2=4х2 – 16х+16; 3х2 – 14х – у2+15=0;
домножим данное выражение на
3) По условию МА=МN. Отсюда, так как N(2; y), то
х2 – 2х+1+у2=х2 – 4х+4; у2= –2х+3;
Аудиторные задания Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой: №84. 9х2+4у2 – 54х – 32у+109=0. Ответ: №85.х2 – у2 – 4х+2у+7=0. Ответ: №86.х2 – 9у2+2х – 36у – 44=0. Ответ: №87.у=х2+4х+5. Ответ: (х+2)2=у – 1. Построить линию, заданную параметрическими уравнениями: №88. №89.
Домашние задания Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой: №90.4х2+9у2 – 8х – 36у+4=0. Ответ: №91.х2 – 9у2+2х+36у – 44=0. Ответ: №92.у=х2 – 5х+7. Ответ: №93.х2+4у2 – 4х – 8у+8=0. Ответ: О(2; 1). №94.х2+4у2+8у+5=0. Ответ: мнимый эллипс. №95.х2 – у2 – 6х+10=0. Ответ: у2 – (х – 3)2=1. №96.х2 – 6х+8=0. Ответ: х=2; х=4. №97.х2+2х+5=0. Ответ: мнимые прямые. Построить линию, заданную параметрическими уравнениями: №98. №99. №100. №101. Ответ: отрезок прямой, соединяющий точки А(1; 0) и В(0; 1).
Дополнительные задания Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой: №102.36х2+36у2 – 36х – 24у – 23=0. Ответ: №103. Ответ: №104.16х2+25у2 – 32х+50у – 359=0. Ответ: №105.у=4х2+8х+7. Ответ: 4(х+1)2=у – 3. Построить линию, заданную параметрическими уравнениями: №106. Ответ: луч, направленный по биссектрисе первого координатного угла. №107. №108. №109. №110. №111.
Занятие 5 Полярная система координат Цели Знать: v Связь между полярной и прямоугольной системой координат; v уравнения основных линий в полярной системе координат. Уметь: v Схематически строить линию в полярной системе координат. Cвязь между полярными и прямоугольными координатами точки устанавливается формулами:
при этом полюс полярной системы координат О совмещен с началом координат системы XOY, а полярная ось — с положительной полуосью ОX (рис.14).
рис.14
Переход от декартовых координат к полярным координатам:
Аудиторное задание Выполнить лабораторную работу «Построение линий в полярной системе координат». Цель работы: приобретение навыков построения линий по уравнению в полярной системе координат.
Задание и общие указания
Инструкция к работе №1. Построить точки в полярной системе координат: ► Отрицательные углы
рис.15
№2. Построить линии: а) в) Провести краткое исследование формы кривой по уравнению: 1) симметрия кривой; 2) область существования кривой; 3) для построения линий в полярных координатах составить таблицу значений ► а) 1) Линия симметрична относительно прямой 2) 3) Составим таблицу с шагом
По данным таблицы построим искомую линию (рис.16).
рис.16
б) 1) линия симметрична относительно полярной оси; 2) 3) составим таблицу с шагом
По данным таблицы построим искомую линию (рис.17).
рис.17
в) 1) линия симметрична относительно полюса О; 2) 3) составим таблицу с шагом
По данным таблицы построим искомую линию (рис.18).
рис.18◄
№3. Записать уравнения линий, заданных в п.2, в декартовой системе координат. ► Используя формулы перехода от полярной системы координат к декартовой (40) имеем: а)
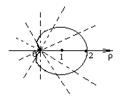
х2+у2=4у; х2+(у – 2)2=4 — уравнение смещённой окружности. б)
в)
(х2+у2)2=2ху — уравнение лемнискаты Бернулли. ◄ №4. Данные уравнения линий в декартовых координатах записать в полярных координатах: а) у2=16+8х; б) ►а) б)
Вариант 1
3)
Вариант 2
Вариант 3
3)
Вариант 4
3)
Вариант 5
Вариант 6
3)
1) Вариант 7
3)
1) Вариант 8
3)
2) Вариант 9 1.Построить точки: 2.Построить линии: 1) 3) 3.Записать в декартовых координатах уравнения п.2. 4.Данные уравнения линий в декартовых координатах записать в полярных координатах: 1) Вариант 10
3)
Домашние задания №112.В полярной системе координат построить точки: А(2; 0); В №113.Написать в полярных координатах уравнения линий: 1) №114.Построить линии: 1) 4) №115.Написать в декартовых координатах уравнения линий и построить линии: 1) 3) Дополнительные задания №116.Построить линии, заданные уравнениями в полярных координатах. Записать в декартовых координатах: 1) 2) 6) 9) 12) №117.Составить в полярных координатах уравнения следующих линий: 1) прямой, перпендикулярной к полярной оси и отсекающей на ней отрезок, равный 3; 2) прямых, параллельных полярной оси и отстоящих от неё на расстоянии 5; 3) окружности R=4 с центром на полярной оси и проходящей через полюс; 4) окружностей радиусом R=3, касающихся полярной оси в полюсе. Ответ: 1) Решение типового варианта индивидуального домашнего задания «Кривые второго порядка»
Задание 1.Составить канонические уравнения: а) эллипса, большая полуось которого равна 3, а фокус находится в точке б) гиперболы с мнимой полуосью, равной 2, и фокусом в) параболы, имеющей директрису х= –3. ►а) Каноническое уравнение эллипса имеет вид б) Каноническое уравнение гиперболы имеет вид в) Каноническое уравнение параболы в данном случае имеет вид у2=2 р х, уравнение её директрисы
Задание 2.Записать уравнение окружности, проходящей через фокусы эллипса х2+4у2=4 и имеющей центр в его верхней вершине. ► Для данного эллипса Радиус искомой окружности вычисляем по формуле расстояния между двумя точками: R=|AF1|=|AF2|= В соответствии с уравнением (15) записываем искомое уравнение окружности: (х – 0)2+(у – 1)2=22 или х2+(у – 1)2=4.◄
Задание 3.Составить уравнение линии, каждая точка М которой отстоит от точки А(3; 2) на расстоянии, в три раза большем, чем от точки В(–1; 0). ► Пусть М(х; у) — любая точка искомой линии (рис.19).
рис.19 Тогда по условию задачи |AM|=3|BM|. Т.к. |AM|=
Преобразуем его, возведя обе части в квадрат. Имеем: х2 – 6х+9+у2 – 4у+4=9х2+18х+9+9у2, 8х2+24х+8у2+4у – 4=0. Выделив полные квадраты в последнем уравнении, придём к уравнению вида:
которое является уравнением окружности с центром в точке Задание 4.Построить кривую, заданную уравнением в полярных координатах ► Составим таблицу, в которой приведены значения полярного угла
Построив найденные точки в полярной системе координат и соединив их плавной линией, получим кардиоиду. ◄ Задание 5. Построить кривую, заданную параметрическими уравнениями:
► Выберем достаточное количество значений параметра t, вычислим соответствующие значения х, у. Построим соответствующие точки в декартовых координатах. Соединим их плавной линией. Очевидно, что полученная кривая является эллипсом с полуосями а=3, b=2 и центром в точке С(1; 2). Для строго доказательства того, что данные параметрические уравнения определяют эллипс с указанными осями и центром, избавимся от параметра t:
Возведём в квадрат оба уравнения системы и сложим их, откуда
Контрольные вопросы
Метод координат на плоскости 1. В каких четвертях могут быть расположены точки М(х; у), если: a) x y>0; b) x y<0; c) y=0; d) x – y>0; f) x+y=0? 2. Точки А(х1; у1) и В(х2; у2) служат смежными вершинами ромба, диагонали которого параллельны осям координат. Как выразить координаты остальных вершин через координаты данных точек? 3. Как расположены точки, имеющие одну и ту же проекцию на ось ОХ ? на ось ОY?
Уравнения прямой на плоскости
а) параллельна оси OY; б) проходит через начало координат?
а)
а) параллельна оси ОX; б) под углом
а) параллельны; б) перпендикулярны?
а) пересекающихся прямых; б) параллельных прямых?
а) имеющих одинаковые угловые коэффициенты и общую точку; б) угловые коэффициенты которых не равны.
Кривые второго порядка
в) е.) 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 — эллипс;
— эллипс; — гипербола,
— гипербола, ,
, ,
, ,
,

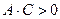 ),
), ),
), ).
). (38)
(38)
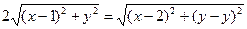 ;
; ;
; ;
; ;
; ;
;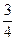 , имеем:
, имеем: — уравнение эллипса, который смещён относительно системы координат XОY, таким образом, что центр эллипса находится в точке
— уравнение эллипса, который смещён относительно системы координат XОY, таким образом, что центр эллипса находится в точке  , точка А — совпадает с правым фокусом, х=2 — правая директриса.
, точка А — совпадает с правым фокусом, х=2 — правая директриса. ;
; ;
; ;
;
 — уравнение гиперболы, которая смещёна относительно системы координат XОY, таким образом, что центр гиперболы находится в точке
— уравнение гиперболы, которая смещёна относительно системы координат XОY, таким образом, что центр гиперболы находится в точке  , точка А совпадает с её левым фокусом, х=2 — левая директриса.
, точка А совпадает с её левым фокусом, х=2 — левая директриса. ;
;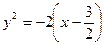 — уравнение параболы, которая смещёна относительно системы координат XОY, таким образом, что вершина находится в точке
— уравнение параболы, которая смещёна относительно системы координат XОY, таким образом, что вершина находится в точке  , точка А совпадает с фокусом, прямая х=2 — директриса. ◄
, точка А совпадает с фокусом, прямая х=2 — директриса. ◄ .
. .
. .
.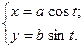 Ответ: эллипс.
Ответ: эллипс. Ответ: астроида.
Ответ: астроида. .
. .
. .
.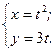 Ответ: парабола у2=9х.
Ответ: парабола у2=9х. Ответ: гипербола
Ответ: гипербола  .
. Ответ: гипербола.
Ответ: гипербола.
 .
. .
.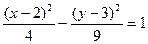 .
. .
.
 Ответ: дуга параболы.
Ответ: дуга параболы.
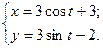


 (39)
(39)
 ;
;  ;
; ;
;  ;
;  . (40)
. (40)
 отсчитываются по часовой стрелке, отрицательные значения
отсчитываются по часовой стрелке, отрицательные значения  откладываются не на луче, наклонённом к полярной оси под углом
откладываются не на луче, наклонённом к полярной оси под углом  ) (рис.15). ◄
) (рис.15). ◄
 ; б)
; б)  ;
; .
. , выбрав шаг
, выбрав шаг  (n — коэффициент перед
(n — коэффициент перед  ;
; , достаточно рассмотреть
, достаточно рассмотреть  ;
; :
:





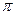

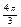





 в виду симметрии кривой;
в виду симметрии кривой; :
:
 или
или 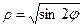 — данная линия лемниската Бернулли.
— данная линия лемниската Бернулли. ;
;  ;
;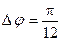 :
:

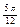




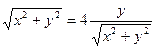 ;
;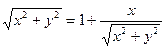 ;
; — уравнение кардиоиды.
— уравнение кардиоиды. ;
; ;
; .
. — уравнение параболы;
— уравнение параболы; ;
; ;
; — уравнение кардиоиды. ◄
— уравнение кардиоиды. ◄ .
.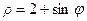 ; 2)
; 2)  ;
;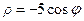 .
.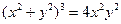 ; 2)
; 2)  .
. .
. ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  .
. .
. ; 2)
; 2)  ;
; .
. ; 2) у=8х.
; 2) у=8х. .
. ; 2)
; 2)  ;
; .
. ; 2)
; 2)  .
. .
. ; 2)
; 2) 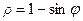 ; 3)
; 3)  .
. ; 2)
; 2)  .
.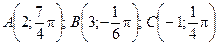 .
.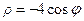 ; 2)
; 2)  ;
; .
. ; 2) х2 – 3у2 – 6х=0.
; 2) х2 – 3у2 – 6х=0. .
. ; 2)
; 2)  ;
;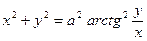 ; 2)
; 2)  .
. .
.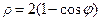 ; 2)
; 2)  ;
; .
.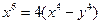 ;
; .
. .
. ; 2)
; 2)  ;
; .
. ; 2)
; 2)  .
. .
. ; 2)
; 2)  ;
; ; 2)
; 2)  .
. ; С
; С  ; D
; D 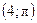 ; E
; E  ; F
; F  ; G
; G 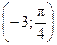 ; K
; K 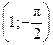 ; L
; L  ; M
; M 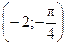 .
.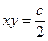 ; 2) у – 2х=0; 3) х2+у2=2а у.
; 2) у – 2х=0; 3) х2+у2=2а у. ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  .
. ; 2)
; 2)  ;
; .
. ; 3)
; 3)  ; 4)
; 4)  ;
; ; 7)
; 7)  ; 8)
; 8)  ;
; ; 10)
; 10)  ; 11)
; 11) 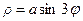 ;
; ; 13)
; 13)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. ;
; ;
;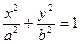 . По условию большая полуось, а=3, с=
. По условию большая полуось, а=3, с=  . Для эллипса: c2=a2 – b2, следовательно, b2=32 –
. Для эллипса: c2=a2 – b2, следовательно, b2=32 – 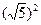 =4. Искомое уравнение:
=4. Искомое уравнение:  ;
; . Для гиперболы: c2=a2+b2, следовательно, а2=с2 – b2=
. Для гиперболы: c2=a2+b2, следовательно, а2=с2 – b2=  – 22=9. Искомое уравнение гиперболы:
– 22=9. Искомое уравнение гиперболы:  .
. , но по условию задачи уравнение директрисы х= – 3, поэтому
, но по условию задачи уравнение директрисы х= – 3, поэтому  ; р=6. Искомое каноническое уравнение параболы имеет вид: у2=12х. ◄
; р=6. Искомое каноническое уравнение параболы имеет вид: у2=12х. ◄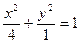 верхняя вершина А(0; 1), а=2, b=1. Поэтому с=
верхняя вершина А(0; 1), а=2, b=1. Поэтому с=  =
=  =
=  . Таким образом, фокусы находятся в точках F1(–
. Таким образом, фокусы находятся в точках F1(– 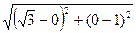 =
=  =2.
=2.
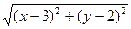 , |BM|=
, |BM|=  , то уравнение искомой линии:
, то уравнение искомой линии: ,
, и радиусом R=
и радиусом R=  . ◄
. ◄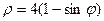 .
.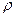 :
:

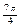
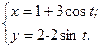

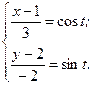
 . ◄
. ◄
 ; б)
; б)  ?
? ?
? .
.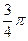 ?
? уравнением прямой в отрезках? Какие отрезки отсекает она на осях координат?
уравнением прямой в отрезках? Какие отрезки отсекает она на осях координат? и
и  так, чтобы прямые 5х – 3у+1=0 и
так, чтобы прямые 5х – 3у+1=0 и  совпадали?
совпадали? с положительным направлением оси ОY? оси ОX?
с положительным направлением оси ОY? оси ОX? образовывала с осью ОY угол
образовывала с осью ОY угол 
 и
и  взаимно перпендикулярны?
взаимно перпендикулярны? ; б)
; б)  ;
; ; д.)
; д.)  ;
;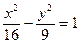 ?
?