|
Кривые, заданные параметрически
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
Всякой линии L на плоскости XOY соответствует некоторое уравнение F(x,y)=0 с двумя переменными x и y . Это уравнение линии L.
Прямая линия на плоскости
Прямая линия  задается уравнением первой степени относительно x и y. задается уравнением первой степени относительно x и y.
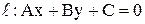 . (6) . (6)
Это общее уравнение прямой  . Здесь коэффициенты А и В есть координаты нормального вектора . Здесь коэффициенты А и В есть координаты нормального вектора  (рис. 21). (рис. 21).
Существуют другие виды уравнения прямой  . Так, решив уравнения (6) относительно у , получим (если . Так, решив уравнения (6) относительно у , получим (если 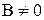 ): ):
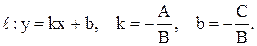 Это уравнение прямой c угловым коэффициентом.
Это уравнение прямой c угловым коэффициентом.
| |  у у
b
О х
 Рис. 21 Рис. 21
Здесь 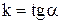 - угловой коэффициент прямой, b – величина отрезка, отсекаемого прямой на оси OY (рис. 21).Если С - угловой коэффициент прямой, b – величина отрезка, отсекаемого прямой на оси OY (рис. 21).Если С  0, то уравнение (6) можно записать в форме 0, то уравнение (6) можно записать в форме
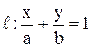 . Здесь а и b - величины отрезков, которые прямая . Здесь а и b - величины отрезков, которые прямая  отсекает на осях ОХ и OY (рис. 21). отсекает на осях ОХ и OY (рис. 21).
Если прямая проходит через две заданные точки 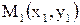 и и 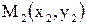 , то ее уравнение имеет вид , то ее уравнение имеет вид 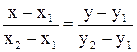 . .
Пример. Прямая  проходит через точки проходит через точки  и и 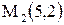 . Написать ее уравнение, найти угловой коэффициент и отрезки, которые она отсекает на осях координат. . Написать ее уравнение, найти угловой коэффициент и отрезки, которые она отсекает на осях координат.
Решение. 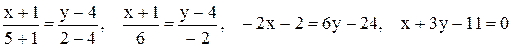 - oбщее уравнение прямой. Отсюда следует, что - oбщее уравнение прямой. Отсюда следует, что 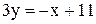 или или 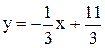 - уравнение прямой с угловым коэффициентом. Здесь - уравнение прямой с угловым коэффициентом. Здесь 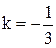 . Из уравнения . Из уравнения  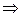 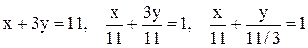 . Итак, а=11, b= . Итак, а=11, b= 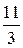 . .
Если прямые 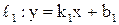 и и 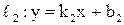 пересекаются в точке М (рис. 22), то угол поворота от пересекаются в точке М (рис. 22), то угол поворота от 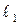 и и 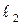 определяется по формуле определяется по формуле
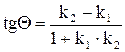 . (7) . (7)
| | | | В частности, если 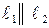 , то , то
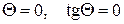 и и 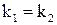 . Если же . Если же 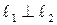 , то , то 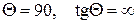 . Из формулы (7) следует, что . Из формулы (7) следует, что 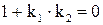 или или 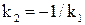 . .
| |

 у у
  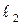 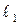
М 

О х
Рис. 22
Пример. Найти угол между прямыми  и и  . .
Решение. Так как 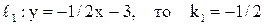 . .
Так как 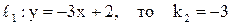 . . 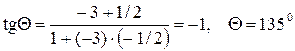 . .
Кривые второго порядка
Так называются линии, которые описываются уравнениями второй степени относительно х и у. К ним относятся окружность, эллипс, гипербола и парабола.
1. Окружность
 - каноническое уравнение,
х, у – текущие координаты окружности,
О – центр окружности,
r – радиус окружности. - каноническое уравнение,
х, у – текущие координаты окружности,
О – центр окружности,
r – радиус окружности.
| |   у у

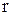
 О х О х
2. 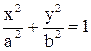 - каноническое уравне-ние , а – большая полуось эллипса, b – малая полуось. - каноническое уравне-ние , а – большая полуось эллипса, b – малая полуось.  - фокусы эллипса. Величины а, b, с связаны формулой - фокусы эллипса. Величины а, b, с связаны формулой 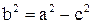 . .
| | Эллипс
 у у
b a
  О c О c   х х

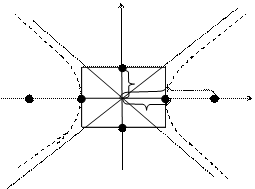
3. 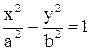 -каноническое уравнение, а – действительная полуось, b - мнимая полуось, -каноническое уравнение, а – действительная полуось, b - мнимая полуось,  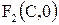 - фокусы гиперболы, - фокусы гиперболы, 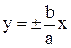 - уравнения асимп-тот; величины - уравнения асимп-тот; величины 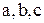 связаны формулой связаны формулой 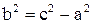 . .
| | Гипербола
 Y Y
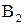
b c
 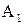 O a O a 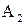  x x

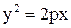 - каноническое уравнение, - каноническое уравнение, 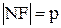 - параметр параболы, О – вершина параболы, - параметр параболы, О – вершина параболы,  - фокус параболы. Прямая - фокус параболы. Прямая 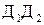 -директриса. Уравнение -директриса. Уравнение 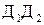 : : 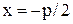 .
Если изменить расположение кривой относите-льно системы координат, то изменится и урав-нение кривой, которое уже не будет каноническим. При этом возможны следующие случаи: .
Если изменить расположение кривой относите-льно системы координат, то изменится и урав-нение кривой, которое уже не будет каноническим. При этом возможны следующие случаи:
| |   4. Парабола 4. Парабола
y

N O F
x
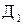 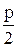 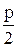
Центр кривой перенесен в точку  без изменения направления осей симметрии. Уравнения полученных кривых называют нормальными. без изменения направления осей симметрии. Уравнения полученных кривых называют нормальными.
  
y  y y 


   

O x O x
 

y  y y

O x  
 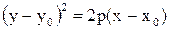
Полярная система координат
Она задается полярной осью 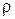 ,на которой указаны начало отсчета О и единица ,на которой указаны начало отсчета О и единица
масштаба (рис.23). 
у
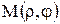
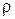 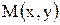
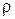 y y
O  O O 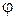
1 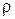 x x 
Рис. 23 Рис. 24
В полярной системе всякая точка М имеет две координаты: расстояние 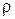 от полюса О до точки М, то есть от полюса О до точки М, то есть 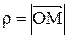 , и угол , и угол 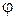 , который образует радиус-вектор , который образует радиус-вектор 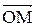 с осью с осью 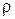 . Числа . Числа  называются полярными координатами точки М. Они изменяются в границах называются полярными координатами точки М. Они изменяются в границах  , , 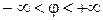 . .
Если полярную систему координат естественным образом совместить с декар-
товой системой XOY (рис. 24), то  . Это формулы, с помощью которых можно перейти от декартовых координат к полярным. Из этих формул следует, что . Это формулы, с помощью которых можно перейти от декартовых координат к полярным. Из этих формул следует, что 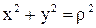 . Таким образом, полярные координаты выгодны в тех случаях, когда уравнение линии . Таким образом, полярные координаты выгодны в тех случаях, когда уравнение линии  содержит выражение содержит выражение 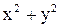 . .
Пример. Уравнение кривой 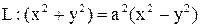 записать в полярных координатах. записать в полярных координатах.
Здесь 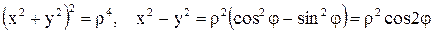 . .
Поэтому 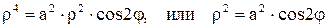 . Эта кривая называется лемнискатой Бернулли (рис. 25). . Эта кривая называется лемнискатой Бернулли (рис. 25).
О  О О 
Рис. 25 Рис. 26
Пример. Построить кривую  . Эта кривая называется кардиоидой (рис. 26). Строим таблицу значений, придавая аргументу . Эта кривая называется кардиоидой (рис. 26). Строим таблицу значений, придавая аргументу 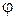 значения значения  с постоянным шагом с постоянным шагом  . .
В обобщенной полярной системе координат допускаются отрицательные значения полярного радиуса 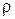 . В этой системе . В этой системе 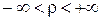 , , 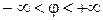 . При этом точки . При этом точки  строятся симметрично относительно полюса О. Например, из уравнения лемнискаты строятся симметрично относительно полюса О. Например, из уравнения лемнискаты 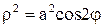 следует, что следует, что  . .
Здесь  . Строим таблицу значений. . Строим таблицу значений.
Уравнению  соответствует та часть лемнискаты, которая расположе-на в первой и четвертой четвертях, а уравнению соответствует та часть лемнискаты, которая расположе-на в первой и четвертой четвертях, а уравнению  - во второй и треть-ей четвертях. - во второй и треть-ей четвертях.
Кривые, заданные параметрически
Линию L на плоскости XOY можно рассматривать как траекторию движущейся точки М (х,у) . При этом ее координаты х и у изменяются в зависимости от некоторого параметра t. Обычно в качестве параметра t выступает либо время движения, либо угол поворота. Таким образом, параметрические уравнение линии L имеют вид 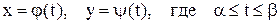 . .
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 у
у

 у
у

 4. Парабола
4. Парабола

 задается уравнением первой степени относительно x и y.
задается уравнением первой степени относительно x и y.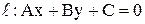 . (6)
. (6) (рис. 21).
(рис. 21).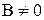 ):
):
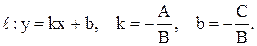 Это уравнение прямой c угловым коэффициентом.
Это уравнение прямой c угловым коэффициентом.
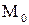
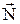
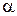
 Рис. 21
Рис. 21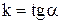 - угловой коэффициент прямой, b – величина отрезка, отсекаемого прямой на оси OY (рис. 21).Если С
- угловой коэффициент прямой, b – величина отрезка, отсекаемого прямой на оси OY (рис. 21).Если С 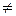 0, то уравнение (6) можно записать в форме
0, то уравнение (6) можно записать в форме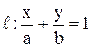 . Здесь а и b - величины отрезков, которые прямая
. Здесь а и b - величины отрезков, которые прямая 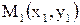 и
и 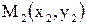 , то ее уравнение имеет вид
, то ее уравнение имеет вид 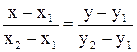 .
. и
и 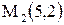 . Написать ее уравнение, найти угловой коэффициент и отрезки, которые она отсекает на осях координат.
. Написать ее уравнение, найти угловой коэффициент и отрезки, которые она отсекает на осях координат.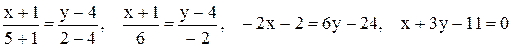 - oбщее уравнение прямой. Отсюда следует, что
- oбщее уравнение прямой. Отсюда следует, что 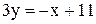 или
или 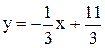 - уравнение прямой с угловым коэффициентом. Здесь
- уравнение прямой с угловым коэффициентом. Здесь 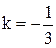 . Из уравнения
. Из уравнения 
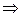
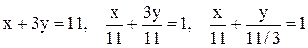 . Итак, а=11, b=
. Итак, а=11, b= 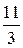 .
.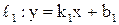 и
и 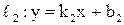 пересекаются в точке М (рис. 22), то угол поворота от
пересекаются в точке М (рис. 22), то угол поворота от 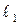 и
и 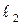 определяется по формуле
определяется по формуле
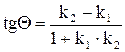 . (7)
. (7)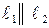 , то
, то
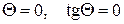 и
и 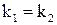 . Если же
. Если же 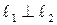 , то
, то 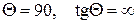 . Из формулы (7) следует, что
. Из формулы (7) следует, что 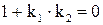 или
или 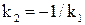 .
.

 у
у



 и
и  .
.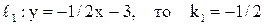 .
.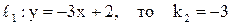 .
. 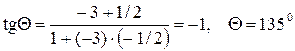 .
. - каноническое уравнение,
х, у – текущие координаты окружности,
О – центр окружности,
r – радиус окружности.
- каноническое уравнение,
х, у – текущие координаты окружности,
О – центр окружности,
r – радиус окружности.

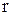
 О х
О х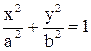 - каноническое уравне-ние , а – большая полуось эллипса, b – малая полуось.
- каноническое уравне-ние , а – большая полуось эллипса, b – малая полуось.  - фокусы эллипса. Величины а, b, с связаны формулой
- фокусы эллипса. Величины а, b, с связаны формулой 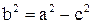 .
.
 у
у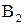
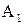
 О c
О c 
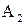 х
х
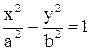 -каноническое уравнение, а – действительная полуось, b - мнимая полуось,
-каноническое уравнение, а – действительная полуось, b - мнимая полуось, 
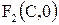 - фокусы гиперболы,
- фокусы гиперболы, 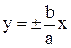 - уравнения асимп-тот; величины
- уравнения асимп-тот; величины 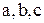 связаны формулой
связаны формулой 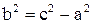 .
.
 Y
Y
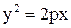 - каноническое уравнение,
- каноническое уравнение, 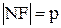 - параметр параболы, О – вершина параболы,
- параметр параболы, О – вершина параболы,  - фокус параболы. Прямая
- фокус параболы. Прямая 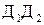 -директриса. Уравнение
-директриса. Уравнение 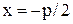 .
Если изменить расположение кривой относите-льно системы координат, то изменится и урав-нение кривой, которое уже не будет каноническим. При этом возможны следующие случаи:
.
Если изменить расположение кривой относите-льно системы координат, то изменится и урав-нение кривой, которое уже не будет каноническим. При этом возможны следующие случаи:

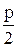
 без изменения направления осей симметрии. Уравнения полученных кривых называют нормальными.
без изменения направления осей симметрии. Уравнения полученных кривых называют нормальными.


 y
y 








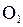
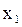


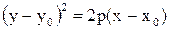
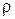 ,на которой указаны начало отсчета О и единица
,на которой указаны начало отсчета О и единица
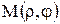
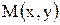
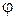 O
O 
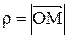 , и угол
, и угол 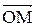 с осью
с осью  называются полярными координатами точки М. Они изменяются в границах
называются полярными координатами точки М. Они изменяются в границах  ,
, 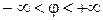 .
. . Это формулы, с помощью которых можно перейти от декартовых координат к полярным. Из этих формул следует, что
. Это формулы, с помощью которых можно перейти от декартовых координат к полярным. Из этих формул следует, что 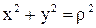 . Таким образом, полярные координаты выгодны в тех случаях, когда уравнение линии
. Таким образом, полярные координаты выгодны в тех случаях, когда уравнение линии  содержит выражение
содержит выражение 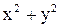 .
.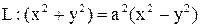 записать в полярных координатах.
записать в полярных координатах.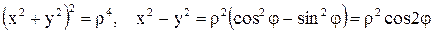 .
.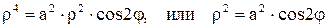 . Эта кривая называется лемнискатой Бернулли (рис. 25).
. Эта кривая называется лемнискатой Бернулли (рис. 25).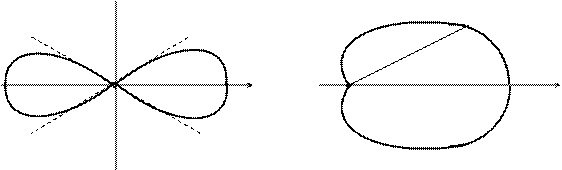
 . Эта кривая называется кардиоидой (рис. 26). Строим таблицу значений, придавая аргументу
. Эта кривая называется кардиоидой (рис. 26). Строим таблицу значений, придавая аргументу  с постоянным шагом
с постоянным шагом  .
.
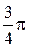
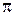

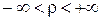 ,
,  строятся симметрично относительно полюса О. Например, из уравнения лемнискаты
строятся симметрично относительно полюса О. Например, из уравнения лемнискаты 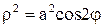 следует, что
следует, что  .
. . Строим таблицу значений.
. Строим таблицу значений.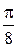
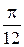

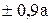

 соответствует та часть лемнискаты, которая расположе-на в первой и четвертой четвертях, а уравнению
соответствует та часть лемнискаты, которая расположе-на в первой и четвертой четвертях, а уравнению  - во второй и треть-ей четвертях.
- во второй и треть-ей четвертях. .
.