Тема: Прямоугольные координаты на плоскости
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
 ЗАДАНИЕ N 1 сообщить об ошибке ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Точка 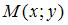 лежит на оси абсцисс и равноудалена от точки лежит на оси абсцисс и равноудалена от точки 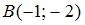 и начала координат. Тогда точка и начала координат. Тогда точка 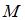 имеет координаты … имеет координаты …
Решение:
Так как точка 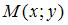 лежит на оси абсцисс, то ее ордината лежит на оси абсцисс, то ее ордината 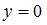 . Так как точка . Так как точка  равноудалена от точки равноудалена от точки 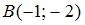 и начала координат и начала координат 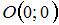 , то расстояния от точки , то расстояния от точки 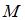 до точек до точек 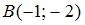 и и 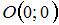 равны. Тогда равны. Тогда  , или , или 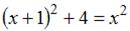 , ,  . То есть . То есть 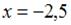 . .
 ЗАДАНИЕ N 2 сообщить об ошибке ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Нормальное уравнение плоскости 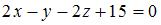 имеет вид … имеет вид …
 ЗАДАНИЕ N 3 сообщить об ошибке ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Прямая задана в параметрическом виде 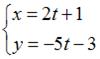 . Тогда ее общее уравнение имеет вид … . Тогда ее общее уравнение имеет вид …
 ЗАДАНИЕ N 4 сообщить об ошибке ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Вершина параболоида 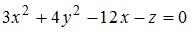 имеет координаты … имеет координаты …
 ЗАДАНИЕ N 5 сообщить об ошибке ЗАДАНИЕ N 5 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Плоскости 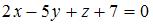 и и 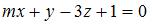 перпендикулярны при значении перпендикулярны при значении 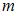 , равном … , равном …
Решение:
Плоскости, заданные общими уравнениями 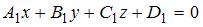 и и  перпендикулярны при условии, что перпендикулярны при условии, что  . Тогда . Тогда  , то есть , то есть 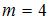 . .
 ЗАДАНИЕ N 6 сообщить об ошибке ЗАДАНИЕ N 6 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
В треугольнике с вершинами 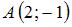 , , 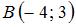 , , 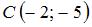 уравнение высоты, проведенной из вершины уравнение высоты, проведенной из вершины 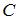 , имеет вид … , имеет вид …
Решение:
Воспользуемся уравнением прямой, проходящей через точку  перпендикулярно нормальному вектору перпендикулярно нормальному вектору 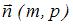 : : 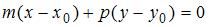 . В качестве нормального вектора возьмем вектор . В качестве нормального вектора возьмем вектор 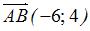 , а в качестве заданной точки возьмем точку , а в качестве заданной точки возьмем точку 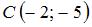 . Тогда . Тогда 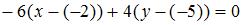 , или , или 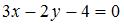 . .
 ЗАДАНИЕ N 7 сообщить об ошибке ЗАДАНИЕ N 7 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Даны уравнения поверхностей второго порядка:
А) 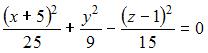
B) 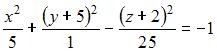
C) 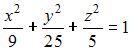
D) 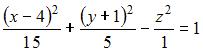
Тогда двуполостный гиперболоид задается уравнением …

|
| | B
|  ЗАДАНИЕ N 8 сообщить об ошибке ЗАДАНИЕ N 8 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Даны вершины треугольника 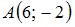 , , 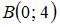 и и  . Тогда координаты точки пересечения медиан треугольника равны … . Тогда координаты точки пересечения медиан треугольника равны …
Решение:
Медианы треугольника пересекаются в одной точке в отношении 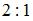 , считая от вершины. Найдем, например, точку , считая от вершины. Найдем, например, точку 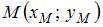 пересечения медианы пересечения медианы 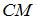 со стороной со стороной 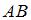 , используя формулы деления отрезка пополам: , используя формулы деления отрезка пополам:  , ,  . .
А координаты точки  пересечения медиан найдем, используя формулы деления отрезка пересечения медиан найдем, используя формулы деления отрезка 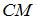 в отношении в отношении 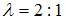 , считая от вершины , считая от вершины  : : 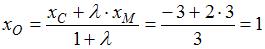 , , 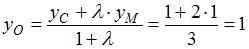 . .
 ЗАДАНИЕ N 26 сообщить об ошибке ЗАДАНИЕ N 26 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Расстояние между точками 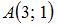 и и 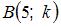 равно 2 при равно 2 при  , равном … , равном …
 ЗАДАНИЕ N 27 сообщить об ошибке ЗАДАНИЕ N 27 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Общее уравнение плоскости, проходящей через точку 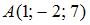 параллельно плоскости параллельно плоскости  , имеет вид … , имеет вид …
 ЗАДАНИЕ N 28 сообщить об ошибке ЗАДАНИЕ N 28 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Площадь треугольника, образованного пересечением прямой 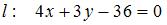 с осями координат, равна … с осями координат, равна …
Решение:
Приведем уравнение прямой 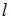 к уравнению прямой «в отрезках»: к уравнению прямой «в отрезках»:  или или 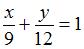 . Уравнение прямой «в отрезках», отсекающей на координатных осях . Уравнение прямой «в отрезках», отсекающей на координатных осях 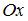 и и 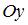 отрезки длиной отрезки длиной  и и 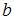 соответственно, имеет вид: соответственно, имеет вид: 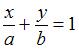 . Следовательно, треугольник, образованный прямой . Следовательно, треугольник, образованный прямой 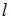 и осями координат – прямоугольный, с вершинами и осями координат – прямоугольный, с вершинами 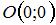 , , 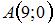 , ,  и гипотенузой и гипотенузой 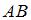 . Площадь треугольника . Площадь треугольника 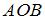 будет равна: будет равна: 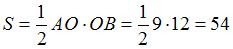 . .
 ЗАДАНИЕ N 29 сообщить об ошибке ЗАДАНИЕ N 29 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Уравнение поверхности второго порядка 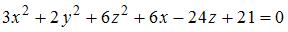 определяет … определяет …

|
| | эллипсоид
|  ЗАДАНИЕ N 14 сообщить об ошибке ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Площадь треугольника, образованного пересечением прямой 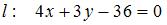 с осями координат, равна … с осями координат, равна …
Решение:
Приведем уравнение прямой 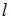 к уравнению прямой «в отрезках»: к уравнению прямой «в отрезках»:  или или 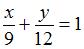 . Уравнение прямой «в отрезках», отсекающей на координатных осях . Уравнение прямой «в отрезках», отсекающей на координатных осях 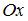 и и 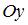 отрезки длиной отрезки длиной  и и 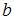 соответственно, имеет вид: соответственно, имеет вид: 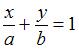 . Следовательно, треугольник, образованный прямой . Следовательно, треугольник, образованный прямой 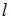 и осями координат – прямоугольный, с вершинами и осями координат – прямоугольный, с вершинами 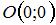 , , 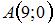 , ,  и гипотенузой и гипотенузой 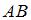 . Площадь треугольника . Площадь треугольника 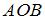 будет равна: будет равна: 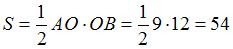 . .
 ЗАДАНИЕ N 15 сообщить об ошибке ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Сфера с центром 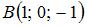 проходит через точку проходит через точку 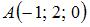 . Тогда ее уравнение имеет вид … . Тогда ее уравнение имеет вид …
Решение:
Уравнение сферы радиуса  с центром в точке с центром в точке 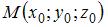 имеет вид имеет вид 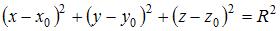 . .
Подставим координаты центра 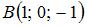 в это уравнение: в это уравнение: 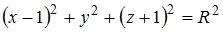 . .
Радиус сферы найдем из условия, что координаты точки 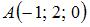 удовлетворяют уравнению сферы: удовлетворяют уравнению сферы: 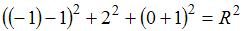 , то есть , то есть 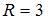 . Тогда уравнение сферы примет вид: . Тогда уравнение сферы примет вид: 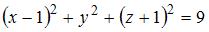 . .
 ЗАДАНИЕ N 16 сообщить об ошибке ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Нормальное уравнение плоскости 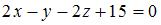 имеет вид … имеет вид …
Решение:
Нормальное уравнение плоскости имеет вид:
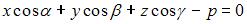 , ,
где  , , 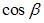 , , 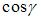 – направляющие косинусы нормали плоскости, направленной из начала координат в сторону плоскости; – направляющие косинусы нормали плоскости, направленной из начала координат в сторону плоскости; 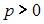 – расстояние от начала координат до плоскости. – расстояние от начала координат до плоскости.
Общее уравнение плоскости 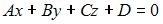 приводится к нормальному виду умножением на нормирующий множитель приводится к нормальному виду умножением на нормирующий множитель 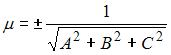 , знак которого берется противоположным знаку свободного члена , знак которого берется противоположным знаку свободного члена 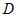 . .
Тогда 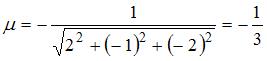 и искомое уравнение имеет вид: и искомое уравнение имеет вид:
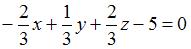 . .
 ЗАДАНИЕ N 17 сообщить об ошибке ЗАДАНИЕ N 17 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Даны точки 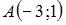 и и  . Тогда координаты точки . Тогда координаты точки 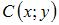 , симметричной точке , симметричной точке  относительно точки относительно точки 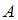 , равны … , равны …
 ЗАДАНИЕ N 31 сообщить об ошибке ЗАДАНИЕ N 31 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Уравнение сферы имеет вид 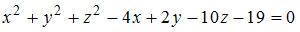 . Тогда радиус сферы равен … . Тогда радиус сферы равен …
 ЗАДАНИЕ N 32 сообщить об ошибке ЗАДАНИЕ N 32 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Даны точки 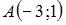 и и  . Тогда координаты точки . Тогда координаты точки 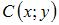 , симметричной точке , симметричной точке  относительно точки относительно точки 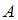 , равны … , равны …
Решение:
Воспользуемся формулой деления отрезка пополам. Координаты точки 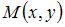 , делящей отрезок между точками , делящей отрезок между точками  и и 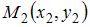 пополам, находятся по формулам пополам, находятся по формулам  ; ; 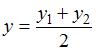 . Тогда координаты точки . Тогда координаты точки 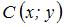 находятся как находятся как 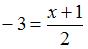 ; ;  , то есть точка , то есть точка 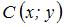 имеет координаты имеет координаты 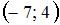 . .
 ЗАДАНИЕ N 33 сообщить об ошибке ЗАДАНИЕ N 33 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Общее уравнение плоскости, проходящей через точку 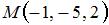 перпендикулярно прямой перпендикулярно прямой 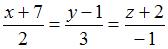 , имеет вид … , имеет вид …
Решение:
Уравнение плоскости, проходящей через точку 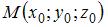 с нормальным вектором с нормальным вектором  , имеет вид: , имеет вид: 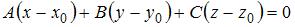 . .
Так как эта плоскость перпендикулярна прямой 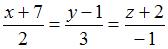 , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть 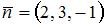 . Тогда . Тогда
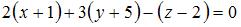 или или 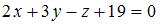 . .
 ЗАДАНИЕ N 34 сообщить об ошибке ЗАДАНИЕ N 34 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Уравнение геометрического места точек, равноудаленных от двух данных точек 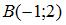 и и 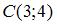 , имеет вид … , имеет вид …
Решение:
Пусть некоторая точка 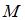 , удовлетворяющая данному условию, имеет координаты , удовлетворяющая данному условию, имеет координаты 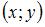 . В этом случае выполняется соотношение . В этом случае выполняется соотношение 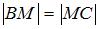 , имеющее вид: , имеющее вид: 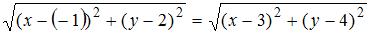 . Тогда . Тогда  , или , или  , ,  . .
То есть 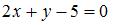 . .
 ЗАДАНИЕ N 1 сообщить об ошибке ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Уравнение плоскости, проходящей через точки 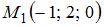 , , 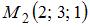 и и  , имеет вид … , имеет вид …
 ЗАДАНИЕ N 2 сообщить об ошибке ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Каноническое уравнение линии пересечения однополостного гиперболоида 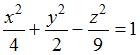 и плоскости и плоскости  имеет вид … имеет вид …
Решение:
Уравнение кривой пересечения однополостного гиперболоида и плоскости получим, решив систему 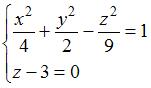 , то есть , то есть 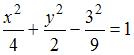 , или , или 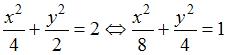 . .
Полученное уравнение есть каноническое уравнение эллипса.
 ЗАДАНИЕ N 3 сообщить об ошибке ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Прямая отсекает на оси 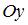 отрезок отрезок 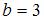 и имеет угловой коэффициент и имеет угловой коэффициент 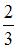 . Тогда ее уравнение имеет вид … . Тогда ее уравнение имеет вид …
 ЗАДАНИЕ N 4 сообщить об ошибке ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
В треугольнике с вершинами 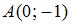 , , 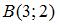 и и 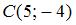 проведена медиана проведена медиана 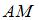 , длина которой равна … , длина которой равна …
 ЗАДАНИЕ N 13 сообщить об ошибке ЗАДАНИЕ N 13 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Уравнение прямой, проходящей через точку пересечения прямых 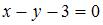 и и 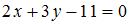 перпендикулярно прямой перпендикулярно прямой 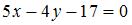 имеет вид … имеет вид …
Решение:
Уравнение прямой, перпендикулярной прямой 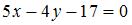 можно определить как можно определить как 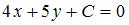 , где для определения , где для определения 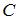 найдем точку пересечения прямых найдем точку пересечения прямых 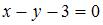 и и 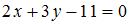 : :
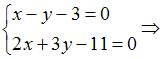 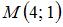 . .
Подставим в уравнение прямой 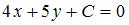 координаты точки координаты точки 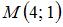 : : 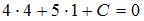 , отсюда , отсюда 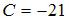 . Тогда уравнение искомой прямой примет вид . Тогда уравнение искомой прямой примет вид  . .
 ЗАДАНИЕ N 14 сообщить об ошибке ЗАДАНИЕ N 14 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
В треугольнике с вершинами 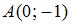 , , 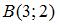 и и 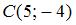 проведена медиана проведена медиана 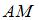 , длина которой равна … , длина которой равна …
 ЗАДАНИЕ N 15 сообщить об ошибке ЗАДАНИЕ N 15 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Центр сферы  имеет координаты … имеет координаты …
Решение:
Уравнение сферы радиуса  с центром в точке с центром в точке 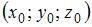 имеет вид: имеет вид: 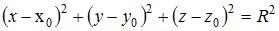 . .
Выделим в исходном уравнении полные квадраты:  , или , или 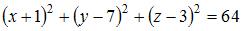 . .
Тогда центр сферы имеет координаты 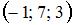 . .
 ЗАДАНИЕ N 16 сообщить об ошибке ЗАДАНИЕ N 16 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Уравнение плоскости, проходящей через точки 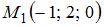 , , 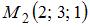 и и  , имеет вид … , имеет вид …
Решение:
Уравнение плоскости, проходящей через точки 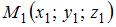 , , 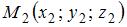 и и 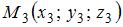 , не лежащие на одной прямой, имеет вид , не лежащие на одной прямой, имеет вид 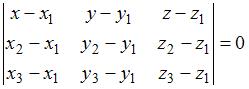 . .
Подставим числовые значения в полученное уравнение: 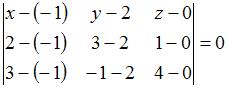 , или , или 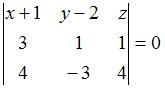 . .
Раскрывая определитель по первой строке, получим 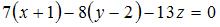 , ,
то есть 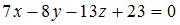 . .
 ЗАДАНИЕ N 1 сообщить об ошибке ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Плоскость в пространстве
Начало формы
   
Конец формы
Геометрическое место точек, удаленных от плоскости  на 2 единицы, может иметь вид … на 2 единицы, может иметь вид …
Решение:
Расстояние от точки  до плоскости до плоскости  находится по формуле находится по формуле 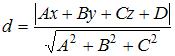 или или 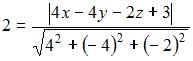 . Тогда . Тогда 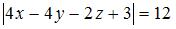 . Отсюда можно получить общее уравнение плоскости, например, в виде . Отсюда можно получить общее уравнение плоскости, например, в виде 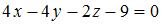 . .
 ЗАДАНИЕ N 2 сообщить об ошибке ЗАДАНИЕ N 2 сообщить об ошибке
Тема: Прямоугольные координаты на плоскости
Начало формы
   
Конец формы
Точки 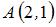 и и  лежат на одной прямой, параллельной оси ординат. Расстояние между точками лежат на одной прямой, параллельной оси ординат. Расстояние между точками 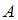 и и 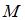 равно 6. Тогда положительные координаты точки равно 6. Тогда положительные координаты точки 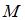 равны … равны …
 ЗАДАНИЕ N 3 сообщить об ошибке ЗАДАНИЕ N 3 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
   
Конец формы
Прямые  и и 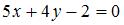 … …

|
| | перпендикулярны
| Решение:
Воспользуемся формулой 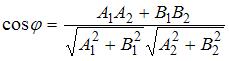 для вычисления угла для вычисления угла 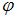 между двумя прямыми: между двумя прямыми:  и и 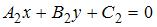 . Тогда . Тогда 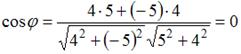 . Следовательно, угол между прямыми равен . Следовательно, угол между прямыми равен 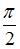 , то есть прямые перпендикулярны. , то есть прямые перпендикулярны.
 ЗАДАНИЕ N 4 сообщить об ошибке ЗАДАНИЕ N 4 сообщить об ошибке
Тема: Поверхности второго порядка
Начало формы
   
Конец формы
Сфера с центром 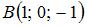 проходит через точку проходит через точку 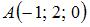 . Тогда ее уравнение имеет вид … . Тогда ее уравнение имеет вид …
Решение:
Уравнение сферы радиуса  с центром в точке с центром в точке 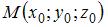 имеет вид имеет вид 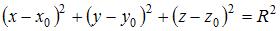 . .
Подставим координаты центра 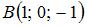 в это уравнение: в это уравнение: 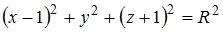 . .
Радиус сферы найдем из условия, что координаты точки 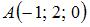 удовлетворяют уравнению сферы: удовлетворяют уравнению сферы: 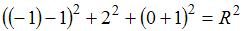 , то есть , то есть 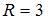 . Тогда уравнение сферы примет вид: . Тогда уравнение сферы примет вид: 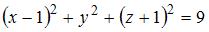 . .
 ЗАДАНИЕ N 1 сообщить об ошибке ЗАДАНИЕ N 1 сообщить об ошибке
Тема: Прямая на плоскости
Начало формы
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ЗАДАНИЕ N 1 сообщить об ошибке
ЗАДАНИЕ N 1 сообщить об ошибке
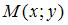 лежит на оси абсцисс и равноудалена от точки
лежит на оси абсцисс и равноудалена от точки 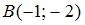 и начала координат. Тогда точка
и начала координат. Тогда точка 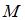 имеет координаты …
имеет координаты …
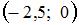
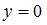 . Так как точка
. Так как точка  равноудалена от точки
равноудалена от точки 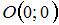 , то расстояния от точки
, то расстояния от точки  , или
, или 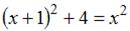 ,
,  . То есть
. То есть 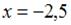 .
.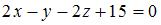 имеет вид …
имеет вид …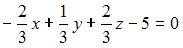
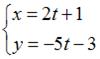 . Тогда ее общее уравнение имеет вид …
. Тогда ее общее уравнение имеет вид …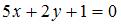
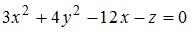 имеет координаты …
имеет координаты …
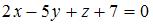 и
и 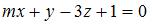 перпендикулярны при значении
перпендикулярны при значении 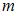 , равном …
, равном …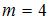
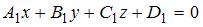 и
и  перпендикулярны при условии, что
перпендикулярны при условии, что  . Тогда
. Тогда  , то есть
, то есть 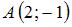 ,
, 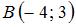 ,
, 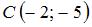 уравнение высоты, проведенной из вершины
уравнение высоты, проведенной из вершины 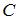 , имеет вид …
, имеет вид …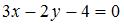
 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 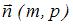 :
: 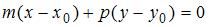 . В качестве нормального вектора возьмем вектор
. В качестве нормального вектора возьмем вектор 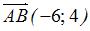 , а в качестве заданной точки возьмем точку
, а в качестве заданной точки возьмем точку 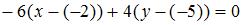 , или
, или 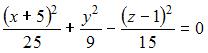
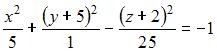
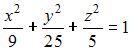
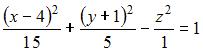
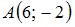 ,
, 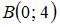 и
и  . Тогда координаты точки пересечения медиан треугольника равны …
. Тогда координаты точки пересечения медиан треугольника равны …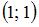
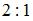 , считая от вершины. Найдем, например, точку
, считая от вершины. Найдем, например, точку 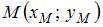 пересечения медианы
пересечения медианы 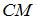 со стороной
со стороной 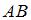 , используя формулы деления отрезка пополам:
, используя формулы деления отрезка пополам:  ,
,  .
. пересечения медиан найдем, используя формулы деления отрезка
пересечения медиан найдем, используя формулы деления отрезка 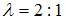 , считая от вершины
, считая от вершины 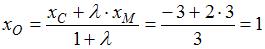 ,
, 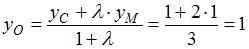 .
.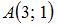 и
и 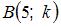 равно 2 при
равно 2 при  , равном …
, равном …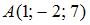 параллельно плоскости
параллельно плоскости  , имеет вид …
, имеет вид …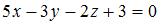
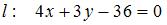 с осями координат, равна …
с осями координат, равна …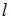 к уравнению прямой «в отрезках»:
к уравнению прямой «в отрезках»:  или
или 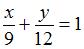 . Уравнение прямой «в отрезках», отсекающей на координатных осях
. Уравнение прямой «в отрезках», отсекающей на координатных осях 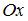 и
и 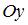 отрезки длиной
отрезки длиной  и
и 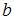 соответственно, имеет вид:
соответственно, имеет вид: 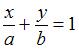 . Следовательно, треугольник, образованный прямой
. Следовательно, треугольник, образованный прямой 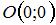 ,
, 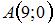 ,
,  и гипотенузой
и гипотенузой 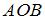 будет равна:
будет равна: 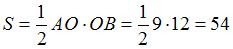 .
.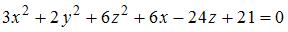 определяет …
определяет …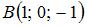 проходит через точку
проходит через точку 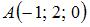 . Тогда ее уравнение имеет вид …
. Тогда ее уравнение имеет вид …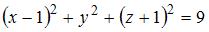
 с центром в точке
с центром в точке 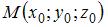 имеет вид
имеет вид 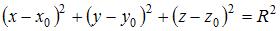 .
. 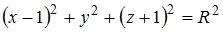 .
. 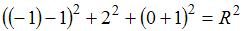 , то есть
, то есть 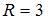 . Тогда уравнение сферы примет вид:
. Тогда уравнение сферы примет вид: 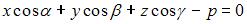 ,
, ,
, 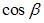 ,
, 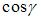 – направляющие косинусы нормали плоскости, направленной из начала координат в сторону плоскости;
– направляющие косинусы нормали плоскости, направленной из начала координат в сторону плоскости; 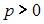 – расстояние от начала координат до плоскости.
– расстояние от начала координат до плоскости.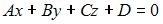 приводится к нормальному виду умножением на нормирующий множитель
приводится к нормальному виду умножением на нормирующий множитель 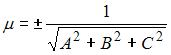 , знак которого берется противоположным знаку свободного члена
, знак которого берется противоположным знаку свободного члена 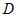 .
.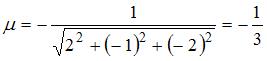 и искомое уравнение имеет вид:
и искомое уравнение имеет вид: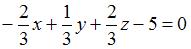 .
.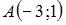 и
и  . Тогда координаты точки
. Тогда координаты точки 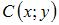 , симметричной точке
, симметричной точке  относительно точки
относительно точки 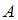 , равны …
, равны …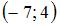
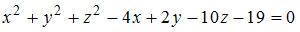 . Тогда радиус сферы равен …
. Тогда радиус сферы равен …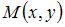 , делящей отрезок между точками
, делящей отрезок между точками  и
и 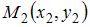 пополам, находятся по формулам
пополам, находятся по формулам  ;
; 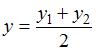 . Тогда координаты точки
. Тогда координаты точки 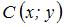 находятся как
находятся как 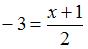 ;
;  , то есть точка
, то есть точка 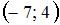 .
.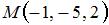 перпендикулярно прямой
перпендикулярно прямой 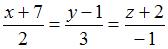 , имеет вид …
, имеет вид …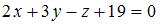
 , имеет вид:
, имеет вид: 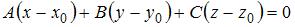 .
.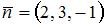 . Тогда
. Тогда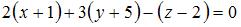 или
или 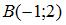 и
и 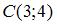 , имеет вид …
, имеет вид …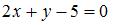
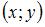 . В этом случае выполняется соотношение
. В этом случае выполняется соотношение 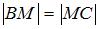 , имеющее вид:
, имеющее вид: 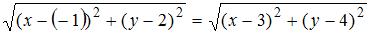 . Тогда
. Тогда  , или
, или  ,
,  .
. 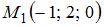 ,
, 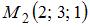 и
и  , имеет вид …
, имеет вид …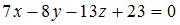
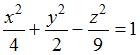 и плоскости
и плоскости  имеет вид …
имеет вид …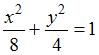
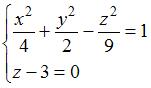 , то есть
, то есть 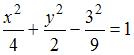 , или
, или 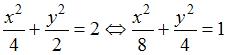 .
. 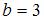 и имеет угловой коэффициент
и имеет угловой коэффициент 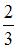 . Тогда ее уравнение имеет вид …
. Тогда ее уравнение имеет вид …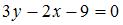
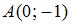 ,
, 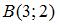 и
и 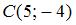 проведена медиана
проведена медиана 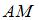 , длина которой равна …
, длина которой равна …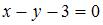 и
и 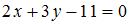 перпендикулярно прямой
перпендикулярно прямой 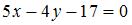 имеет вид …
имеет вид …
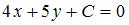 , где для определения
, где для определения 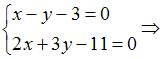
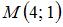 .
. 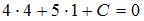 , отсюда
, отсюда 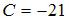 . Тогда уравнение искомой прямой примет вид
. Тогда уравнение искомой прямой примет вид  имеет координаты …
имеет координаты …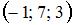
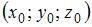 имеет вид:
имеет вид: 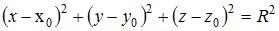 .
. , или
, или 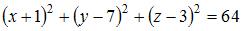 .
.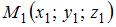 ,
, 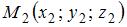 и
и 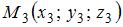 , не лежащие на одной прямой, имеет вид
, не лежащие на одной прямой, имеет вид 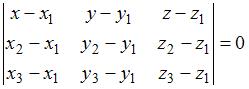 .
. 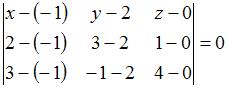 , или
, или 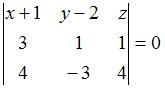 .
. 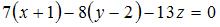 ,
, на 2 единицы, может иметь вид …
на 2 единицы, может иметь вид …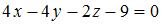
 до плоскости
до плоскости  находится по формуле
находится по формуле 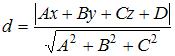 или
или 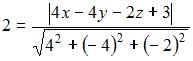 . Тогда
. Тогда 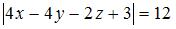 . Отсюда можно получить общее уравнение плоскости, например, в виде
. Отсюда можно получить общее уравнение плоскости, например, в виде 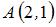 и
и  лежат на одной прямой, параллельной оси ординат. Расстояние между точками
лежат на одной прямой, параллельной оси ординат. Расстояние между точками  ,
, 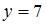
 и
и 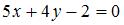 …
…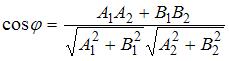 для вычисления угла
для вычисления угла 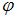 между двумя прямыми:
между двумя прямыми:  и
и 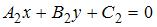 . Тогда
. Тогда 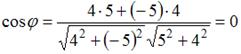 . Следовательно, угол между прямыми равен
. Следовательно, угол между прямыми равен 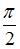 , то есть прямые перпендикулярны.
, то есть прямые перпендикулярны.