
|
|
Необходимые и достаточные условия существования безусловного экстремума.Функции нескольких переменных (ФНП). Предел ФНП в точке и его свойства. Повторные пределы. Непрерывность ФНП в точке и на множестве. Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие f, которое каждой паре чисел (х;у) ? D сопоставляет одно и только одно число 2 ? Е, называется функцией двух переменных, Примером функции двух переменных может служить площадь S прямоугольника Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой. Свойства 1.Предел суммы (разности) двух функций равен сумме (разности) их пределов 2.Предел произведения двух функций равен произведению их пределов 3.Постоянный множитель можно выносить за знак предела 4.Предел степени с натуральным показателем равен той же степени предела 5.Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю
2. Дифференциал ФНП. Геометрический смысл дифференциала функции двух переменных. Дифференциал сложной функции. Инвариантность формы первого дифференциала.
Дифф. сложной ф-ции нескольких переменных. U=f(x,y,z); x=x(t), y=y(t), z=z(t) U=f(x(t),y(t),z(t))=F(t) Теорема: Если ф-цияU=f(x,y,z) дифф. В т. Po(xo,yo,zo) принадл. D(f), а x=x(t), y=y(t), z=z(t) - дифф. в т. To прин. D(f), то U=f(x(t),y(t),z(t)) будет дифф. в т. To прин. D(f), и
Производная сложной функции. Неявные функции и их дифференцирование. dz/dt=dz/dx*dx/dt+dz/dy*dy/dt формула сложной производной. Функция z=f(x,y) наз. Заданной неявно, если она определена равенством, неразрешенным относительно z . F(x,y,z)=0 x+y+z=ez - это равенство задаем некоторую функцию z=f(x,y), которую нельзя выразить в полном виде. x2+y2+z2=0 - не задает никакой функции. Теорема: Если ф-я F(x,y,z) непрерывна в т. р0(x0,y0,z0) и ее производная по z Fz(x,y,z)0, то равенство F(x,y,z)=0 однозначно определяет в неявном виде функцию z=f(x,y), при этом эта функция дифференцируема и ее производная находится по формулам: z/x= Fx(x,y,z)/Fz(x,y,z) z/y=Fz (x,y,z)/Fy(x,y,z) Док-во: Найдем полный дифференциал функции dF(x,y,z)=F/x*dx+F/y*dy+F/x*dz F(x0,y0,z0)=0dF=0 F/x*dx+F/y*dy+F/x*dz=0 dz=(F/x)/(F/z)*dx(F/y)/(F/z)*dy (*) С другой стороны: z=f(x,y), dz=z/x*dx+z/y*dy (**) Сравнивая (*) и(**) z/x= Fx(x,y,z)/Fz(x,y,z) z/y=Fz (x,y,z)/Fy(x,y,z)
Касательная плоскость и нормаль к поверхности.
Формула касательной к плоскости: z-z0 = f'x(xo;y0) (х - х0) + fy (х0;уо) {у - у0)
Формула нормали поверхности в точке М (х0,у0)
Линии и поверхности уровня. Производная по направлению. Градиент. Линии уровня ф-ии 2 перемен наз совокупность точек плоск в кот эта ф-ия имеет одинаковое значение. Линии уровня 3 перемен наз совокупность точек пр-ва в кот эта ф-ция u=F(x,y,z) имеет постоянное значение с и опред ур-нием F(x,y,z)=c. Производная dz/dl=dz/dx cosα+dz/dycosβ определяет велечину скорости измен ф-ии z(М) при движении М по направлению L. Градиентом ф-ии z=f(x) в данной точке М0(x0,y0) наз вектор имеющ своим началом эту точку коорд кот явл частные произв этой ф-ии в М0. Grad z(M0)=dz/dx(M0) i(вект)+dz/dy(M0) j(вект) следовательно dz/dl=/grad z/ cosα, где α угол между векторами grad z и l.Теорема. Градиент ф-ии z=f(x,y) в М0(x0,y0) характеризует направление и величину максимального роста этой ф-ии в М0. Производные и дифференциалы высших порядков.
Если функция
Формула Тейлора для функции двух переменных. Пусть дана ф-ия z=f(x,y) имеющ неприрывн частные производные всех порядков до n+1 включительно в некот окрестн т М0(x0,y0). Формула Тейлора для ф-ии 2 переменных: f(x0+дельта x, y0+дельта y)= f(x0,y0)+df(x0,y0)+(d^2f(x0,y0))/2!+…+(d^n f(xn,yn))/n!+(d^n+1 f(x0+Qдельта x, y0+Qдельта y))/(n+1)!. Определение экстремума ФНП, Необходимое и достаточное условия существования экстремума. Точка хо,y0 называется точкой максимума функции z —f/(x,y), если существует такая из этой окрестности выполняется неравенство f(x) <f(хо). Аналогично определяется точка минимума функции: Необходимые и достаточные условия существования безусловного экстремума. Необходимое условие Если в точке N(xo,у0) дифференцируемая функция z = f(x;y) имеет экстремум, то ее частные производные в этой точке равны нулю
Достаточное условие Пусть встационарной точке (х0;уо) и некоторой ее окрестности функция f(x;y) имеет непрерывные частные производные до второго порядка включительно.
Вычислим в точке (xо;yо) значенияА = C=
.Тогда: 1) если максимум, если А < 0; минимум, если А >0; 2) если В случае Необходимы дополнительные исследования.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

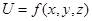
 ;
;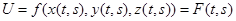
 ;
; 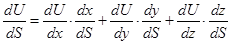
 ;
;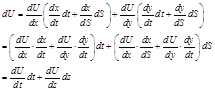
 - свойство инвариантности формы первого дифф.
- свойство инвариантности формы первого дифф.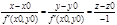

 имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:
имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так:  .
.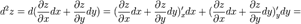

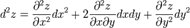

 -окрестность точки хо,y0, что для всех х
-окрестность точки хо,y0, что для всех х  x0
x0 (x0,y0) = 0,
(x0,y0) = 0,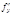 (x0,y0) = 0.
(x0,y0) = 0. (xo;yo), В =
(xo;yo), В =  (xo;yo)
(xo;yo) (xo;yo)
(xo;yo)  =AC-BB
=AC-BB