
|
|
Базис векторного пространства.Определение вектора, его длины, коллинеарных векторов. Вектор– это направленный отрезок. Вектор обозначается как ͞а. Его можно отложить от точки, тогда он имеет начало (вектор АВ, А - начало вектора, В - конец). Вектор имеет две характеристики: длину и направление. Длина вектора а называется модулем вектора и обозначается |а|. Векторы равны, если равны их длины, и они сонаправлены (направлены в одну сторону). Нулевой вектор – вектор, начало и конец которого совпадают; его длина равна нулю, направление неопределенное. Векторы, лежащие на одной прямой или на параллельных прямых называются коллинеарными. Направление не имеет смысла, вектор коллинеарен всем векторам.
Определение суммы, разности векторов, их свойства. Суммой двух векторов ͞а и ͞bназывается вектор ͞с, который может быть найдет по правилу треугольников или параллелограммов. Правило треугольников. Правило параллелограммов. Свойства суммы: 1. ͞a + ͞b = ͞b + ͞aпереместительный (коммутативный) закон. 2. ͞a + (͞b + ͞c) = (͞a + ͞b) + ͞cсочетательный закон 3. ͞0 + ͞а = ͞а(͞а = ͞А͞В) 4. ͞а + (-͞а) = 0(-͞а = ͞В͞А) Разностью векторов ͞а и ͞bявляется такой вектор ͞с, который в сумме с вектором ͞b даёт вектор ͞а.
͞a – ͞b = ͞a + (-͞b), т.е. вычитание векторов производится путем сложения вектора ͞а и вектора (-͞b).
Определение произведения (умножения) вектора на число и его свойства. Произведением вектора ͞a на число αназывается вектор, который обладает двумя свойствами. 1. |α͞а| = |α||͞а| 2. α > 0 => ͞a ↑↑ α͞a α < 0 => ͞a ↑↓ α͞a Свойство умножения: 1. 0͞а = 0 2. (α1)(α2 ͞а) = (α1α2)͞а 3. α (͞а+͞b) = α͞a + α͞bраспределительный закон Вектор называется единичным, если его длина равна 1 (|͞е| = 1). Всякий вектор можно представить в виде произведения длины этого вектора на орт этого вектора. ОРТ – единичный вектор сонаправленный с данным. ͞а = |͞а| ͞е
Первый признак коллинеарности двух векторов (с доказательством). Теорема (признак коллинеарности двух векторов). Для того чтобы не нулевые векторы ͞a и ͞b были коллинеарными необходимо и достаточно чтобы существовало единственное число α такое, что ͞а = α͞b. ͞а ≠ ͞0, ͞b ≠ ͞0 Доказательство. I. Необходимость. Дано: ͞a||͞b Доказать: что существует такое α, при котором ͞а = ͞bα. а) ͞а↑↑͞b 1. ͞a = |͞a|͞e 2. ͞b = |͞b| ͞e |: |͞b| (1/|͞b|)͞ b = ͞e ͞a = (|͞a|/|͞b|) ͞b α = |͞a|/|͞b| (͞а = α1 ͞b, ͞a = α2 ͞b => |α1 ͞b| = |α2 ͞b| => |α1| ͞|b| = |α2| |͞b| => |α1|=|α2| => α1=α2) Имеют одинаковые знаки. б) а ↑↓ b α = - (a/b) II. Достаточность. Дано: существует α, при котором ͞a = α͞b Доказать: ͞а || ͞b Доказательство следует из определения произведения вектора на число. Линейная зависимость векторов и её свойства. Второй признак коллинеарности векторов. Возьмем конечную систему векторов: ͞а1, ͞а2, … , ͞аn ͞α1, ͞α2, … , ͞αn принадлежат R ͞b = α1 ͞a1 + α2 ͞a2 + … + αn ͞an – линейная комбинация векторов ai (i = 1…n). Рассмотрим равенство: *α1 ͞a1 + α2 ͞a2 + …+ αn ͞an = ͞0 Если это равенство справедливо только когда все αi =0, то система векторов ai называется линейно независимая. Если же выполняется равенство * и при этом среди чисел αi есть хотя бы одно отличное от 0, то система векторов называется линейно зависимая. Свойства: Если система содержит хотя бы один 0, то эта система линейно зависима. Доказательство: а1=0 α1 ͞а1 + ͞0 ͞а2 + … + ͞0 ͞a3 = ͞0 Если система векторов содержит линейно зависимую подсистему, то она линейна зависима. Для того чтобы два вектора были линейно зависимыми, необходимо и достаточно, чтобы они были коллинеарными. Три вектора называются компланарными, если они параллельны одной и той же плоскости. 4. Признак компланарности трех векторов. Три вектора линейно зависимы тогда и только тогда, когда она компланарны. Всякие 4 вектора пространства линейно зависимы. Векторы линейно зависимы тогда и только тогда, когда один из них является линейной комбинацией остальных векторов. Теорема. Второй признак коллинеарности векторов. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. I. Необходимость. Дано: ͞a || ͞b Доказать: координаты пропорциональности. ͞а = {a1, a2, a3} ͞b = {b1, b2, b3} ͞a || ͞b => ͞a = α͞b (из первого признака коллинеарности) α – коэффициент пропорциональности a1 = αb1 a2 = αb2 А это и означает, что координаты пропорциональны. а3 = αb3 Обратная теорема доказывается «снизу вверх». Базис векторного пространства. Множество всех векторов параллельных какой-либо прямой называется одномерным векторным пространством (V1). Множество всех векторов параллельных какой-либо плоскости называется двумерным векторным пространством (V2). Множество всех векторов пространства называется трехмерным векторным пространством. Базисом векторного пространстваназывается упорядоченная система векторов, которая удовлетворяет двух условиям: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

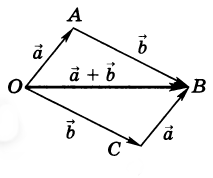
 Разность всегда направлена к уменьшаемому.
Разность всегда направлена к уменьшаемому.