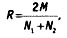Этап 9. Кодирование собранного материала и оценка валидности данных

Обучив персонал и отладив кодовый план, можно проводить кодировку основной выборки рекламных объявлений. После того как этот процесс завершен, необходимо оценить надежность кодировки. Под надежностью (достоверностью) в контент-анализе понимается высокая вероятность того, что два и более кодировщика, работая независимо друг от друга, присвоили одни и те же коды одним и тем же элементам в каждом из проанализированных рекламных объявлений. Данный тип надежности, называемый межкодировочной надежностью, может вычисляться по разным методам, но должен быть обязательно проверен до анализа полученных данных. Низкий уровень вычисленной надежности свидетельствует о том, что полученным данным доверять нельзя.

Холсти¹ для вычисления межкодировочной надежности для номинальных категорий рекомендует крайне простую формулу:

Как видно, метод понятный, простой в вычислениях, однако имеющий тенденцию завышать надежность кодировки, так как не учитывает, что коды могут совпасть и случайно. Допустим, у нас категория имеет две размерности (да — нет). Нетрудно видеть, что, закодировав выборку два раза (имитируя работу двух кодировщиков) с помощью генератора случайных чисел, мы получим надежность, равную примерно 50%. Для решения этой проблемы существуют и другие, более сложные формулы. Однако и они не универсальны, поскольку чувствительны к другим аспектам кодировки. Например, в π-индексе² надежность вычисляется с коррекцией на случайные совпадения:

¹Подробнее см.: Holsti О. Content Analysis for the Social Sciences and Humanities. Reading, MA: Addison-Wesley Publishing Co., 1969.

²Подробнее см.: Scott W. Reliability of Content Analysis: The Case of Nominal Scale Coding. Public Opinion Quarterly, № 61,1955. P. 483-492.

где R — показатель надежности (Reliability), M — общее количество совпавших кодовых элементов у двух кодировщиков, N_l N₂ — общее количество закодированных элементов у 1-го и 2-го кодировщика соответственно. Например, если в 80 случаях из 100 мнения кодировщиков совпали, то надежность по Холсти составляет:

где π — оценка надежности, К₀ — процент наблюдаемых совпадений кодировщиков, К_е — процент ожидаемых совпадений. Недостаток данного индекса состоит в его чувствительности к виду распределения закодированных элементов. Хотя методика его подсчета крайне проста: на первом этапе вычисляется процент ожидаемых совпадений, далее по формуле Холсти вычисляется процент наблюдаемых совпадений. Подставляя эти величины в формулу, мы и получим π-индекс. Например, в нашем гипотетическом примере с чистящими средствами основные рекламируемые выгоды распределились следующим образом (%):

• цена — 30,
• соотношение цена/качество — 25,
• чистящие способности — 15,
• концентрация —10,
• другое —10,
• не обнаружено — 10.

Тогда процент ожидаемых совпадений равен 0,205 (0,30² + 0,25² + 0,15² + 0,10⁰² + 0,10² + 0,10² = 0,205), а процент наблюдаемых совпадений возьмем из предыдущего примера — 80%. Тогда:

Перро и Лей^[1] разработали другой подход к коррекции межкодировочной надежности. Эта формула также не свободна от недостатков, в частности, она зависит от количества размерностей в категории. В каноническом виде она выглядит следующим образом:

где F₀ — количество совпавших кодовых элементов, N — общее количество кодовых элементов, k — количество размерностей в категории. Например, взяв предыдущие данные, мы получим F₀ = 80, N = 100, k = 6. Оценка надежности по Перро-Лею составит:

¹Подробнее см.: Perreauit W.D., Leigh L.E. Reliability of Nominal Data Based on Qualitative Judgments//Journal of Marketing Research. 1989. 26. P. 135—148.

Но, пожалуй, одной из наиболее часто применяемых мер согласия является «каппа Коэна» (Cohen's kappa)², вычисляемая по формуле:

где π_jj — вероятность того, что кодировщик 1 закодирует объект размерностью і, а кодировщик 2 закодирует этот же объект размерностью j. Или, другими словами, это разность между долями согласных и несогласных ответов, деленная на разность между 1 и долей несогласных ответов:

Понятно, что каппа (() может изменяться от 1 (полное согласие двух кодировщиков в оценке объектов) до -1 (полное несогласие). Особый случай, когда каппа равна 0. Это означает, что с таким же успехом можно было бы попросить оценить объекты два генератора случайных чисел.

²Подробнее см.: Cohen J. A coefficient of agreement for nominal scales. Educational and Psychological Measurement. 1960. 20. 37—46.

Все вышеприведенные формулы предназначены для номинальных категорий, и все в той или иной мере используются в контент-анализе. Но, независимо от используемой формулы, приемлемым считается уровень надежности не менее 80%.

Для оценки надежности порядковых и интервальных категорий используются обычные корреляции и ранговые корреляции. Однако здесь существует опасность ошибки при оценке надежности, связанная с тем, что корреляционные коэффициенты указывают направление связи, ничего не говоря о самих значениях. Предположим, мы оцениваем по 5-балльной шкале уровень эмоциональных мотиваций в рекламе, где 1 — «полное отсутствие эмоциональных мотиваций», а 5 — «наличие только эмоциональных мотиваций» (табл. 6):

Таблица 6. Пример таблицы сопоставления оценок различных кодировщиков

Считаем коэффициент ранговой корреляции. Получаем +1.0, надежность стопроцентная, хотя даже на глаз видно, что кодировщик 1 гораздо ниже оценивает наличие эмоциональных мотивов в рекламе.

Не нашли, что искали? Воспользуйтесь поиском по сайту: