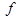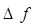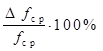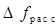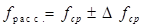|
|
Пусть свет падает на линзу слева.Лабораторная работа. № 1
ОПРЕДЕЛЕНИЕ ФОКУСНОГО РАССТОЯНИЯ ЛИНЗ.
Цель работы: Научиться получать изображения с помощью линз. Ознакомиться с различными методами измерения фокусного расстояния линз. Оборудование: Оптическая скамья с рейтерами, собирающая и рассеивающая линзы, зрительная труба, экран, предмет (миллиметровая сетка), линейка метровая, прямоугольник.
Теория
При прохождении света через границу двух сред (например, стекло-воздух) нарушается прямолинейность его распространения, и говорят, что лучи преломляются. Под лучом понимают направление распространения световой энергии. Совокупность лучей образует пучок. Если лучи при своем продолжении пересекаются в одной точке, то они называются гомоцентрическими. Пучок лучей, составляющий малый угол с оптической осью, называется параксиальным. Примером преломляющих поверхностей служат различные линзы. Прямая, на которой лежат центры сферических поверхностей линзы, называется главной оптической осью линзы. Лучи, падающие на линзу параллельно главной оптической оси, после преломления в линзе сходятся в одной точке, лежащей на главной оптической оси. Эта точка называется главным фокусом линзы. Расстояние от главного фокуса до оптического центра линзы называется фокусным расстоянием линзы. Плоскость, проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. В зависимости от формы и среды, в которой они находятся, линзы делятся на собирающие (положительные) и рассеивающие (отрицательные). Линза называется тонкой, если толщина ее мала по сравнению с радиусом кривизны поверхности. Любой луч, проходящий через точку О практически не испытывает преломления. Эта точка О носит название оптического центра линзы (рис.1).
Рис.1. Для вывода формулы тонкой линзы рассмотрим преломление на сферической поверхности. Пусть два однородных прозрачных вещества с показателями преломления n1 = 1 иn разделены сферической поверхностью с радиусом кривизны r . Проведем главную оптическую ось, которая соединяет точечный источник света S с центром кривизны сферической поверхности С1 (рис.2).
Рис.2. Из точки S проведем любой параксиальный луч, падающий на сферическую поверхность в точке М. Прямая, соединяющая точки М и С1, будет радиусом I-й сферической поверхности, а, следовательно, перпендикуляром к сферической поверхности. Обозначим угол падения луча SM на границу раздела через a , тогда по закону преломления преломляющий луч пересечет главную оптическую ось в точке S1 , угол преломления обозначим через b . По закону преломления при n1=1 Углы между лучами: падающим, преломленным и главной оптической осью обозначим соответственно Для параксиальных лучей формула (1) будет иметь вид:
Из SMC1 Из C1MS1 Подставив (3) в (2), получим: Из точки М опустим перпендикуляр МК на оптическую ось. Для параксиальных лучей Р1К Из треугольников SMK, KMC1 и KMS1 имеем:
Полученные значения углов (5) подставим в (4) и сразу левую и правую части сократим на h. Тогда имеем:
Правая часть выражения (6) зависит только от радиуса кривизны и показателей преломления двух сред n1 = 1 и n , т.е. в течение опыта остается величиной постоянной. Эта величина носит название оптической силы первой преломляющей поверхности и обозначается D1 .
Eсли взять вторую сферическую преломляющую поверхность на границе раздела двух сред n и n2 = 1, то точка S1 будет уже предметом для второй преломляющей поверхности, а S2 ее изображение (рис.2). Проведя аналогичные рассуждения для второй сферической поверхности, получим:
где
- оптическая сила второй сферической преломляющей поверхности. Зная, что оптическая сила всей системы равна
сложим левые и правые части выражений (6) и (8):
Обозначим расстояние Р1 Р2 = l , где l - толщина линзы. Для тонких линз
Правая часть выражения (12) называется оптической силой тонкой линзы
Физический смысл выражения (13) - оптическая сила не зависит от расстояний, а зависит только от формы линзы и показателей преломления линзы и окружающей среды. Величина, обратная оптической силе линзы, называется фокусным расстоянием линзы. Если фокусное расстояние измеряется в метрах, то оптическая сила - в диоптриях.
Подставляя выражения (13) и (14) в формулу (12), получим:
Физический смысл выражений (15) и (16) - если изменяется положение предмета относительно линзы, то положение изображения определяется однозначно. В формулах (15) и (16) используется следующее правило знаков: для всех действительных величин - их расстояния a ; b и f берутся со знаком "+"; для всех мнимых величин - знак "-". Рассмотрим применение формулы (13) к линзе любого вида. Пусть нам дана линза с радиусами кривизны r1 и r2 . Условимся считать r положительным, если световой пучок встречается с выпуклой сферической поверхностью, и r - отрицательным, если световой пучок падает на вогнутую поверхность. На рис.3. показано получение выпукло-вогнутой линзы:
Рис.3. Пусть свет падает на линзу слева. Из рисунка видно: r1> 0; r2 > 0; Тогда так как
Следовательно, такого вида линза будет собирающей, если nл > nср . Если же nл < nср , то т.е. линза, помещенная из воздуха в более плотную среду, чем стекло, становится по своим действиям рассеивающей. Рассмотрим применение формулы (13) к линзе другого вида. Пусть нам дана линза с радиусами кривизны r1 и r2 . Для линзы вогнуто-выпуклой имеем:
Рис.4. Свет падает на линзу слева. Из рисунка видно: r1> 0; r2 > 0; Следовательно,
Если т.е. эта же линза, помещенная в более плотную среду, чем стекло, становится по своим действиям собирающей. Можно показать, что при изменении направления падающего светового потока, т.е. справа на линзу, свойства линзы не изменяются, т.е., если она имела D < 0 при освещении слева, то при освещении справа D остается < 0. Методика измерения. I. ОПРЕДЕЛЕНИЕ ФОКУСНОГО РАССТОЯНИЯ ТОНКОЙ ПОЛОЖИТЕЛЬНОЙ ЛИНЗЫ.
Способ I-й. Фокусное расстояние тонкой положительной линзы можно определить, исходя из формулы линзы (16). Для этого достаточно измерить расстояния от предмета до линзы а и от линзы до изображения b и затем вычислить фокусное расстояние f. При измерениях на одном конце оптической скамьи за осветителем находится прозрачная миллиметровая сетка, выполняющая роль предмета. На другом конце оптической скамьи расположен рейтер с экраном. Между экраном и предметом поместите исследуемую линзу. Перемещая линзу вдоль скамьи, получите на экране четкое изображение предмета. Затем по линейке измерьте расстояния a и b . Измерения выполняются не менее трех раз при различных положениях предмета относительно линзы. Рекомендуется два измерения выполнить при увеличенном, а одно при уменьшенном изображении. Данные занесите в таблицу 1. Таблица 1.
Выполнить построения изображений для данных случаев в рабочей тетради.
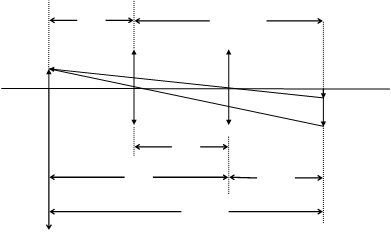
Способ II-й. При описанном выше методе оказывается существенно, чтобы указатель на рейтере линзы был расположен против ее середины. Опишем способ, при котором положение указателя не сказывается на результате измерений. Пусть расстояние между предметом и экраном превышает 4F. Нетрудно убедиться, что при этом всегда найдутся два таких положения линзы, при которых на экране получаются отчетливые изображения предмета (в одном случае - уменьшенное, в другом - увеличенное). Измерение фокусного расстояния тонкой линзы по методу "смещения" (метод Бесселя) показано на (рис.5).
а b
l
a1 b1
L Рис.5. Из соображений симметрии ясно, что a =b1 и b = a1 (рис.5). Обозначая расстояние между предметом и экраном через L, а расстояние между двумя положениями линзы через l , получим: L = a +b ; l=b-a=a1-b1 Отсюда Подставляя (17) в формулу линзы, найдем после несложных преобразований
Для определения фокусного расстояния достаточно, таким образом, измерить расстояние L между предметом и экраном и расстояние l между двумя положениями одной и той же линзы, при которых на экране получаются четкие изображения. Измерения следует проводить с линзой, которая применялась в предыдущем опыте. Опыт производится при трех расстояниях L . Полученные данные внесите в таблицу 2.
Таблица 2.
Выполнить построение для данного случая в рабочей тетради. Способ III-й. В н и м а н и е!!! Напряжение на осветительной лампе уменьшить до 50 В!!! Фокусное расстояние тонкой положительной линзы можно определить с помощью зрительной трубы, установленной на бесконечность. Такую установку проще всего осуществить, наводя трубу на достаточно удаленный предмет (например, на окно противоположного дома). Затем изображение предмета (мм сетка), полученного с помощью собирающей линзы, рассматривают через зрительную трубу. Передвигая линзу, установите ее так, чтобы в окуляре трубы появилось отчетливое изображение предмета. Поскольку труба настроена на бесконечность, и, следовательно, сфокусирована на параллельный пучок лучей, отчетливое изображение появляется при совмещении предмета с фокальной плоскостью линзы. Расстояние между предметом и серединой линзы равно для тонкой линзы фокусному расстоянию. Опыт проводится не менее трех раз. Данные внесите в таблицу 3. Таблица 3.
Выполнить построение для данного случая в рабочей тетради. Фокусное расстояние тонкой положительной линзы, измеренное тремя способами внесите в таблицу 4 и вычислить его истинное значение.
Таблица 4.
II. ОПРЕДЕЛЕНИЕ ФОКУСНОГО РАССТОЯНИЯ ОТРИЦАТЕЛЬНОЙ (РАССЕИВАЮЩЕЙ) ЛИНЗЫ. Способ IV-й. Определение фокусного расстояния рассеивающей линзы с помощью собирающей линзы. Постройте изображение предмета с помощью рассеивающей линзы, и убедитесь, что полученное изображение будет всегда мнимое, значит получить его на экране нельзя. Чтобы определить экспериментально фокусное расстояние рассеивающей линзы надо всегда использовать еще и собирающую линзу, но с оптической силой большей, чем у рассевающей линзы: т.е. В качестве предмета в работе используется прозрачная миллиметровая сетка, которая освещается лампой ФОС (фотометрическая оптическая скамья). Если на пути лучей, идущих от прозрачного предмета (мм сетка) S, поставить собирающую линзу L 1 , то на экране D 1 можно получить изображение предмета S1 . (см. рис.6).
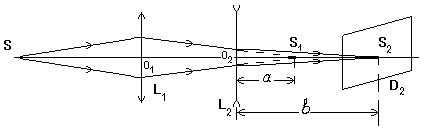
Рис.6. Если теперь между собирающей линзой L 1 и экраном D 1 поставить рассеивающую линзу L 2, а затем убрать экран D1 , закрепив рейтер экрана на месте, то, подбирая новое положение рассеивающей линзы L 2, можно получить действительное изображение предмета на экране D 2, который расположен на расстоянии 20-30 cм от рассеивающей линзы. (При проведении опыта экран D2 - неподвижен). (См. рис.7).
Рис.7. Обозначив расстояния О2 S1 = a; О2 S2 =b, Для данного случая запишем формулу Откуда: Измерьте расстояния Результаты измерений внесите в таблицу 5.
Таблица 5.
Фокусное расстояние собирающей линзы взять из таблицы 4. Постройте ход лучей для данного луча в рабочей тетради, используя масштаб.
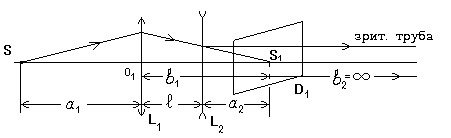
Способ V-й. Определение фокусного расстояния рассеивающей линзы при помощи зрительной трубы. С помощью собирающей линзы L 1 получите на экране действительное изображение S1 . (См. предыдущий способ).
Рис.8. Если теперь поместить рассеивающую линзу L 2 между собирающей линзой L 1 и экраном D1 так, чтобы точка S1 совпала с передним фокусом рассеивающей линзы L 2 , то изображение S 2 (см.рис.6) переместится в бесконечность, т.е. лучи после преломления в рассеивающей линзе пойдут параллельным пучком. Если на пути параллельного пучка поставить зрительную трубу, сфокуси-рованную на бесконечность, то в нее должен быть резко виден предмет S. Таким образом, вначале необходимо получить на экране D 1 четкое изображение S1 предмета S с помощью собирающей линзы L 1 . Затем между этим изображением S1 (экраном D1 ) и собирающей линзой L 1 поместить рассеивающую линзу L 2, убрать экран D1 , закрепив рейтер. В н и м а н и е!!! Напряжение на осветительной лампе уменьшить до 50 В!!! С конца оптической скамьи рассматривать изображение с помощью зрительной трубы, сфокусированной на бесконечность. Перемещая рассеивающую линзу вдоль оптической скамьи добейтесь четкого изображения предмета в зрительной трубе. При этом условии расстояние от точки S1 (положение экрана D1 ) до рассеивающей линзы можно считать ее фокусным расстоянием. Измерения провести не менее 3-х раз, при различных положениях собирающей линзы L 1 относительно предмета S .
Результаты измерений внесите в таблицу 6. Таблица 6.
Начертить ход лучей для данного случая с учетом масштаба, в рабочей тетради..
К о н т р о л ь н ы е в о п р о с ы. 1. Дать определения оптических характеристик линзы: оптический центр, главная оптическая ось, фокус, фокусное расстояние, фокальная плоскость, побочная оптическая ось. 2. Какие лучи надо использовать при построении изображения в линзах? 3. Построить изображение предметов в собирающей и рассеивающей линзе для всех случаев и для точки, находящейся на главной оптической оси. Записать формулу линзы для всех случаев. 4. Вывести формулу тонкой линзы (12). 5. Дать определение оптической силы линзы и ее единицы измерения. 6. Знать и уметь объяснить вывод формулы (18). 7. Объяснить физический смысл выражений (13), (14), (15) и (16). 8. Что означает настройка зрительной трубы на бесконечность? 9. Как изменится изображение, если закрыть половину линзы?
Литература:
1. Г.С.Ландсберг Оптика., М., "Наука", 1976. 2. Е.М.Гершензон и др. Курс общей физики. Оптика и атомная физика. М., "Просвещение", 1981. 3. Ф.А.Королев Курс физики. Оптика, атомная и ядерная физика. М., "Просвещение", 1974. 4. Д.В.Сивухин Общий курс физики. Оптика. "Наука", 1980. 5. С.Э.Фриш и А.В.Тиморева. Курс общей физики. т.Ш, 1961.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ;
;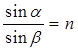 . (1)
. (1) . Угол между радиусом МС1 и оптической осью через d
. Угол между радиусом МС1 и оптической осью через d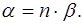 (2)
(2)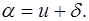
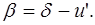 (3)
(3)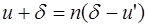 . (4)
. (4) О. Введем обозначения SP1 =a 1 ; P1 S1 =b 1 ; P1 C1 = r1 .
О. Введем обозначения SP1 =a 1 ; P1 S1 =b 1 ; P1 C1 = r1 .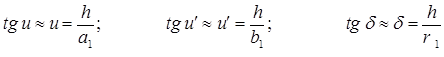 (5)
(5)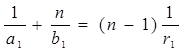 (6)
(6)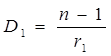 . (7)
. (7)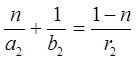 , (8)
, (8)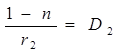 (9)
(9)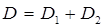 , (10)
, (10)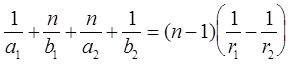 . (11)
. (11)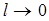 , следовательно, выражение (11) запишется:
, следовательно, выражение (11) запишется: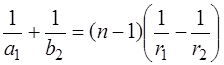 . (12)
. (12)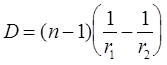 . (13)
. (13)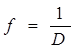 . (14)
. (14)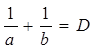 , (15)
, (15)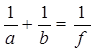 . (16)
. (16)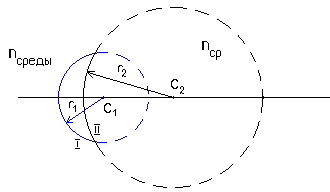
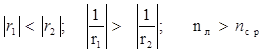 .
.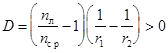 ,
,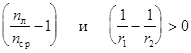
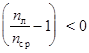 и D < 0,
и D < 0,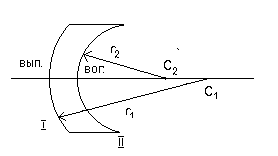
 .
.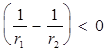 и при
и при 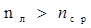 оптическая сила тонкой линзы:
оптическая сила тонкой линзы: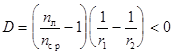 - линза рассеивающая.
- линза рассеивающая.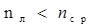 , то
, то  и тогда D > 0,
и тогда D > 0,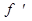
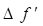
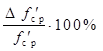
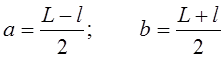 . (17)
. (17)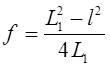 . (18)
. (18)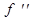


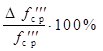
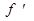 I способ
I способ
 II способ
II способ
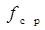
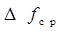

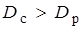 . В этом случае оптическая сила системы линз будет положительной и тогда в такой системе можно получить действительное изображение на экране. В противном случае система в целом будет работать как рассеивающая линза и не даст действительного изображения объекта.
. В этом случае оптическая сила системы линз будет положительной и тогда в такой системе можно получить действительное изображение на экране. В противном случае система в целом будет работать как рассеивающая линза и не даст действительного изображения объекта.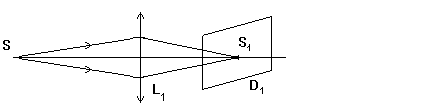
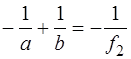 .
. . (19)
. (19)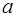 и
и  не менее 3-х раз при различных положениях линз L 1 и L 2, определите фокусное расстояние рассеивающей линзы L 2.
не менее 3-х раз при различных положениях линз L 1 и L 2, определите фокусное расстояние рассеивающей линзы L 2.