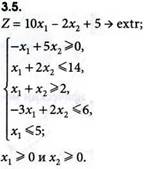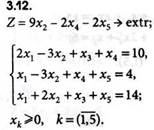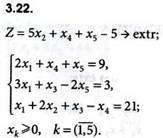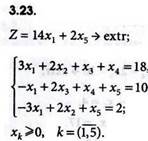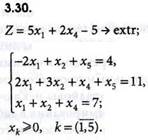|
|
ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ12 Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач с двумя независимыми переменными х1 и х2 и когда ограничениями являются неравенства. Порядок решения задачи линейного программирования графическим способом заключается в следующем: 1. На плоскости в координатных осях х1 о х2 строятся прямые соответствующие исходным ограничениям — неравенствам. 2. Указываются полуплоскости, удовлетворяющие каждому из ограничений. 3. Определяется многоугольник решений, указывая координаты вершин на нем, который называется областью допустимых решений (ОДР). Вычисляются значения целевой функции во всех вершинах многоугольника решений. Выбирая наибольшее и наименьшее значения из вычисленных величин, определяются экстремальные значения целевой функции. 4. Экстремальные величины можно определить непосредственно, построив линию уровня, полагая Z = 0 или принимая значение целевой функции Z = const. ∂Z ∂Z Определяется grad Z: градиент целевой функции grad Z = -----; = ----- ∂х1 ∂х2 направление которого указывает возрастание целевой функции и является перпендикуляром к линиям уровня. Перемещая линию уровня в направлении grad Z до вершины ОДР (точки касания), можно найти максимальное значение целевой функции. Если перемещать линию уровня в направлении противоположном grad Z, то в точке касания к ОДР найденное значение целевой функции соответствует минимальному значению. Пример 3.1 Найти графически экстремальные значения целевой функции: (3.1)
при линейных ограничениях-неравенствах:
(3.2)
и условиях: (3.3)
Решение Так как каждое ограничение-неравенство графически представляет полуплоскость, то пересечение этих полуплоскостей определяет область допустимых решений (ОДР) задачи линейного программирования. Для определения ОДР заменяем нестрогие неравенства системы (3.2) уравнениями (3.4) и строим соответствующие прямые в координатных осях ххох2 (рис. 3.1):
(3.4) Многоугольником решений является пятиугольник АВСДЕ, координаты точек которого удовлетворяют ограничениям (3.2) и условиям неотрицательности (3.3). Координаты вершин пятиугольника соответствуют базисным решениям задачи, которые называются опорными решениями. Среди этих решений находятся и оптимальные решения, которые можно определить двумя способами. I способ. Определяем координаты вершин многоугольника решений АВСДЕ и подставим в целевую функцию. Точка А получена в результате пересечения прямых (2) и (5) системы (3.4):
Рис. 3.1
Подставляя эти координаты в функцию (3.1), получаем
Аналогично определяем координаты вершин многоугольника решений В, С, D и Е, а также значения целевой функции в этих точках. точка В:
точка С:
точка D:
точка Е:
Выделяя наибольшее значение и наименьшее
целевой функции, определяем II способ позволяет определять непосредственно положение точек А и Д соответствующие экстремальным значениям целевой функции.
Определяем градиент целевой функции
Построим линию уровня, пологая Z = 0, т.е. -4x1 + 10х2 = 0. Эта линия перпендикулярна grad (-4; 10) рис. 3.1. Перемещая линию уровня в направлении градиента Z до точки А, которая, являясь касательной к ОДР, определяет максимальное значение целевой функции.
Перемещая линию уровня в направлении противоположном grad Z = = (-4; 10), она займет положение опорной линии в точке
Пример 3.2 Построить на плоскости область решений системы линейных неравенств (3.6) и условий (3.7). Определить максимальное и минимальное значения линейной функции (3.8) в этой области:
(3.6)
(3.7)
(3.8)
Решение 1) Заменяем знаки неравенств на знаки точных равенств, получаем систему уравнений (3.9):
(3.9)
2). Построим соответствующие прямые (3.9) на плоскости в координатных осях Х1ОХ2 и определим область допустимых решений, удовлетворяя ограничениям (3.6). 3). Многоугольником решений является пятиугольник ABCDE, координаты точек которого удовлетворяют условиям (3.7) и неравенствам системы ограничений (3.6) задачи.
4) Для определения точек, соответствующих экстремальным значениям функции (3.8), построим линию уровня 6х1 - 4х2 = 0 и grad Z (6; -4). Перемещая линию уровня в направлении grad Z до точки ее касания к ОДР в точке В, определим максимальное значение целевой функции в этой точке. Вычислим координаты точки В, решая систему:
Перемещая линию уровня параллельно самой себе в направлении противоположном grad Z, она займет положение опорной прямой на отрезке АЕ (так как прямая (4) параллельна линии уровня). Следовательно, в точках А и Е функция принимает минимальные значения.
Определим координаты точки А, решая систему:
Целевая функция в точке А имеет значение:
Искомая функция в токе Е с координатами х1 = 0 и х2 = 3 равна: ZE = 6∙0-4∙3 = -12. Следовательно, в любой точке отрезка АЕ линейная функция имеет одинаковые значения Zmin = -12. Ответ: {-12; 52}. Пример 3.3 Определить экстремальные значения линейной функции Z = - 4x1 + 10х2 (3.10) при линейных ограничениях: (3.11)
и условиях: (3.12)
Решение Находим область допустимых решений, заменяя систему неравенств (3.10) уравнениями (3.13) (рис. 3.3):
(3.13) Областью допустимых решений является открытая область ABC. Определяем координаты точки В, решая систему:
Рис. 3.3
Вычисляем целевую функцию в точке
Передвигая прямую 4х1 + 10х2 = 0 параллельно самой себе в направлении grad (-4;10), она уходит в
Ответ: Пример 3.4 Графическим методом может быть решена задача линейного программирования, у которой система ограничений имеет n неизвестных m уравнениями, которые связаны соотношением n – m = 2. Найти экстремальные значения целевой функции Z = x1+ 4x2 - 2x4 + 5 → extr (3.14) при линейных ограничениях-равенствах:
(3.15)
и условиях:
Решение 1. Для системы (3.14) составляем расширенную матрицу А, ранг которой равен 3.
2. Выделяем базисные переменные х3, х4 и х5, используя метод Жордана - Гаусса:
(3.17) На основании полученной матрицы (3.14) ограничения задачи перепишем в виде: (3.18)
Выделяя базисные переменные х3, х4, х5, систему (3.18) перепишем в виде: (3.19)
Подставляя значения переменных в целевую функцию 3.14, получаем:
Опуская базисные переменные х3 ≥ 0, х4 ≥ 0 и х5 ≥ 0 в системе (3.19), получаем задачу линейного программирования в виде: Z = 5х1 - 2х2 - 5 → extr (3.20) при ограничениях-неравенствах
(3.21) и условиях х1 ≥0,х2 ≥ 0 (3.22) Задачу линейного программирования (3.20)-(3.22) решаем графически. Построим четырехугольник ОАВС решений, grad Z и линию уровня 2х1 — 2х2 —5 = 0, которые позволяют найти максимальное (в точке В) и минимальное (в точке Л) значения целевой функции (рис. 3.4).
Вычисляем значение целевой функции:
Координаты точки А: Определяем координаты точки В, решая систему:
Рис. 3.4
Для отыскания оптимального плана исходной задачи подставим в (3.18) найденные значения для х1 и х2. Для максимальной величины целевой функции базисные переменные имеют значения:
Для минимального значения целевой функции базисные переменные имеют следующие величины:
Контрольные вопросы: 1. Какие задачи линейного программирования решаются графическим методом? 2. Что называется областью допустимых решений? 3. Как определяется положение линии уровня? 4. С какой целью определяется градиент целевой функции? 5. Сущность графического метода решения задач линейного программирования. 6. Геометрический смысл задач линейного программирования. ЗАДАЧИ 3.1-3.10
Решить задачи линейного программирования графическим методом:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


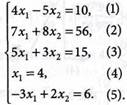

 (3.5)
(3.5) Решая систему (3.5), получаем
Решая систему (3.5), получаем




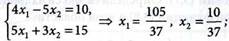








 что соответствует минимальному значению целевой функции, т.е.
что соответствует минимальному значению целевой функции, т.е.

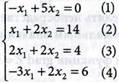








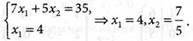


 Следовательно, целевая функция ограничений на максимум не имеет.
Следовательно, целевая функция ограничений на максимум не имеет.


 (3.16)
(3.16)