
|
|
Графический метод решения задачи линейного программированияКафедра математики
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА Линейное программирование для студентов 2 курса дневной формы обучения
Чита – 2009
Печатается по решению учебно-методической комиссии ЧИ БГУЭП Протокол № ______ от __ ________ 2009г. Составитель: старший преподаватель кафедры математики Трухина Л. И. Рекомендовано к печати кафедрой математики Протокол заседания № __ от___________ 2009г. Введение
Линейные модели являются одним из наиболее активно используемых классов математических моделей. Они сравнительно просты, хорошо разработаны, допускают полное исследование и достаточно эффективны в целом ряде стандартных ситуаций. Линейное программирование – это математический метод решения задачи оптимального распределения имеющихся ресурсов (денег, материалов, времени) для достижения определённой цели (наибольшего дохода или наименьших издержек). Программирование в данном термине имеет смысл планирования. Линейное означает, что ищется экстремум линейной целевой функции при линейных ограничениях (линейных уравнениях или линейных неравенствах). Общие ситуации, в которых линейное программирование применяется часто и эффективно: задачи о составлении смеси, цель которых заключается в выборе наиболее экономичной смеси ингредиентов (руды, нефти, пищевых продуктов и др.) при учёте ограничений на физический или химический состав смеси и на наличие необходимых материалов; задачи производства, целью которых является подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья; задачи распределения, цель которых состоит в том, чтобы организовать доставку материалов от некоторого числа источников к некоторому числу потребителей так, чтобы оказались минимальными либо расходы по этой доставке, либо время затрачиваемое на неё, либо некоторая комбинация того и другого. В простейшем виде это задача о перевозках (транспортная задача). Наиболее распространённым методом решения задачи линейного программирования является симплекс-метод. В простейшем случае, когда число переменных равно двум, удобен простой и наглядный графический метод.
Общая задача линейного программирования Задача линейного программирования состоит в составлении плана максимизирующего или минимизирующего некую линейную функцию при ограничениях в виде линейных уравнений или линейных неравенств: найти вектор и удовлетворяющий условиям Линейная функция Любое решение системы ограничений ЗЛП называется допустимымпланом. Допустимый план, максимизирующий или минимизирующий целевую функцию называется оптимальным. План, у которого отличным от нуля компонентам соответствует система линейно независимых векторов, называется опорным планом. Теорема. Множество планов задачи линейного программирования является выпуклым множеством. Теорема. Оптимальный план задачи линейного программирования находится в крайней точке выпуклого множества планов. Если оптимальный план находится в двух крайних точках выпуклого множества планов, то он находится также и в любой точке, являющейся выпуклой комбинацией этих крайних точек.
Формы ЗЛП Форма задачи линейного программирования, у которой ограничения заданы в виде неравенств, называется стандартной, а форма задачи, у которой ограничения заданы в виде уравнений – канонической. Если же система ограничений содержит и уравнения и неравенства, то такая форма называется смешанной.
Графический метод решения задачи линейного программирования
Если задача содержит только две переменные, а система ограничений задана в виде неравенств, то её можно решить графическим методом. Графический метод решения ЗЛП состоит из следующих этапов. 1. Строится область допустимых решений (ОДР). 2. Строится вектор-градиент целевой функции (вектор, координатами которого являются частные производные функции) с приложением в начале координат – 3. Линия уровня C1x1+C2x2 = а (а – постоянная величина) - прямая, перпендикулярная вектору–градиенту 4. Для нахождения ее координат достаточно решить систему из двух уравнений прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,x2), найденное в полученной точке, является максимальным. При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то целевая функция f(x1,x2) не ограничена на максимум (в задаче максимизации) или минимум (в задаче минимизации). Если линия уровня параллельна какой-либо прямой из ограничений задачи, то оптимальное значение целевой функции будет достигаться в любой точке этой прямой. Пример.Найти максимальное значение функции f=2x1 + 3x2 при условиях
Построим область допустимых значений: 1) первое ограничение x1 + 3x2 £ 18; прямая x1 + 3x2 = 18 пересекает оси координат в точках (0; 6) (18; 0); неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка(0; 0), 0 + 3*0 < 18 принадлежит полуплоскости); 2) второе ограничение 2x1 + x2 £ 16: прямая 2x1 + x2 = 16 пересекает оси координат в точках (0; 16) (8; 0); неравенству соответствует полуплоскость, содержащая данную прямую и лежащая ниже неё (контрольная точка (0; 0), 2*0 + 0 <16 принадлежит полуплоскости); 3) неравенству x2 £ 5 соответствует полуплоскость, содержащая прямую x2 = 5 и лежащая ниже неё. 4) x1 ³ 0 - правее ОX2; 5) x2 ³ 0 - выше ОX1. Вектор-градиент имеет координаты Построим линии уровня 2x1 + 3 x2 = а. При а = 0 получим прямую 2x1 + 3x2 = 0, проходящую через начало координат, перпендикулярно вектору-градиенту. Так как задача на максимум, то передвигаем линию уровня в направлении градиента. Предельной точкой (последней из области допустимых решений, с которой соприкасается линия уровня) является точка С. Значит, в ней достигается максимум функции f (рис. 1). Найдём её координаты. Для этого решим систему, составленную из уравнений прямых пересекающихся в точке С (I и II):
Таким образом, получим x1 = 6, x2 = 4, fmax = 2*6 + 3*4 = 24.
Рис. 1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
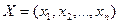 , максимизирующий (минимизирующий) функцию
, максимизирующий (минимизирующий) функцию (1)
(1) (2)
(2) называется целевой функцией задачи. Условия (2) называются ограничениями задачи.
называется целевой функцией задачи. Условия (2) называются ограничениями задачи.



 ,
,
 ,
,
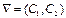 .
. – передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
– передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
 .
.

