
|
|
Линейная функция и её график
Рене Декарт внёс в математику две важных идеи. Первая состоит в том, что, расположив на плоскости две перпендикулярные числовые прямые, мы получаем декартову систему координат, в которой каждая точка получает две координаты (х; у). Вторая – в том, что каждое уравнение описывает в декартовой системе координат некоторую линию. Как пример рассмотрим линейную функцию. Линейная функция задаётся уравнением вида y = k∙x + b, а иногда и более общей формулой с1∙x + с2∙y + с3 = 0 (с1∙и с2∙не равны нулю одновременно), в которой переменная у не выражена явным образом через переменную х. Важно то, что переменные х и у входят в оба уравнения в первой степени. Теорема. Графиком линейной функции является прямая, тангенс угла наклона которой равен k.
Рассмотрим три точки лежащих на графике нашей функции (0; b), (х1; kх1) и (х2; kх2). На чертеже с ними связаны светло-серый и серый прямоугольные треугольники. Если их острые углы при вершине (0; b) не равны, то точки не лежат на одной прямой, и график линейной функции прямой не является. Однако это не так. Поскольку Задача 1. На декартовой плоскости заданы две точки (х1; у1) и (х2; у2). Получить уравнение прямой, проходящей через них. Решение. Поскольку уравнение прямой имеет вид y = k∙x + b нужно найти параметры k∙и b. По условию задачи имеют место равенства y1 = k∙x1 + b и y2 = k∙x2 + b. Система двух линейных уравнений с двумя неизвестными позволяет найти числа k∙и b. Задача 2. Заданы две прямые y = k1∙x + b1 и y = k2∙x + b2. Нужно найти координаты точки их пересечения. Решение. Нужно решить систему линейных уравнений y=k1∙x+b1 и y=k2∙x+b2. Задача 3 Заданы точки А (х1; у1), В (х2; у2), С (х3; у3), D (х4; у4). Нужно найти координаты точки пересечения прямых АС и ВD. Решение. Нужно последовательно решить задачи 1 и 2. Задача 4. На декартовой плоскости задана точка (х0; у0) и тангенс угла наклона прямой k. Получить уравнение прямой, проходящей через заданную точку и заданный тангенс угла наклона. Решение. Поскольку уравнение прямой имеет вид y = k∙x + b и параметр k известен, нужно найти параметр b. Для этого следует подставить в уравнение координаты точек и выразить b. Поскольку b = y0 – k∙x0, уравнение y = k∙x + y0 – k∙x0 можно привести либо к виду В аналитической геометрии часто нужно решать вопрос о взаимном расположении двух и более прямых. Две прямые параллельны, если они образуют с осью абсцисс равные углы. Из этого следует, что две прямые y = k1∙x + b1 и y = k2∙x + b2 параллельны, если k1∙= k2∙и b1 ≠ b2 (если же и b1 = b2, то прямые совпадают). Задача 5. Задана точка (х0; у0) и прямая y = k∙x. Получить уравнение прямой, проходящей через заданную точку параллельно заданной прямой. Решение. Используя задачу 4 и замечание о параллельности прямых, получаем уравнение Задача 6. Задана точка (х0; у0) и прямая y = k∙x. Получить уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой.
Используя задачу 4, получаем уравнение
Решение. Положим ∆х = х2 – х1 и ∆у = у2 – у1. Тогда по аналогии с предыдущей задачей х3 = х2 – ∆у и у3 = у2 + ∆ х. Кроме того, х4 = х1 – ∆у и у4 = у1 + ∆х. Площадь квадрата равна (∆х)2 + (∆у)2. Это следствие теоремы Пифагора. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Доказательство. Рассмотрим формулу с1∙x + с2∙y + с3 = 0. Если с2 неравно нулю, то уравнение приводится к виду y = k∙x + b. В противном случае оно задаёт вертикальную прямую
Доказательство. Рассмотрим формулу с1∙x + с2∙y + с3 = 0. Если с2 неравно нулю, то уравнение приводится к виду y = k∙x + b. В противном случае оно задаёт вертикальную прямую  . Итак мы можем рассматривать уравнение вида y = k∙x + b.
. Итак мы можем рассматривать уравнение вида y = k∙x + b. треугольники подобны, соответствующие острые углы у них равны, а, значит, все три точки лежат на одной прямой. При этом угол наклона этой прямой α таков, что tg α = k.
треугольники подобны, соответствующие острые углы у них равны, а, значит, все три точки лежат на одной прямой. При этом угол наклона этой прямой α таков, что tg α = k. , либо к виду
, либо к виду  , где ∆х = х – х0 (приращение аргумента) и ∆у = у – у0 (приращение функции).
, где ∆х = х – х0 (приращение аргумента) и ∆у = у – у0 (приращение функции). Решение. Прямая y = k∙x проходит через начало координат и через точку (1; k). С этими двумя точками связан прямоугольный треугольник, катеты которого являются приращениями ∆х = 1 (горизонтальный катет) и ∆у = k (вертикальный катет). При повороте данного треугольника на 90° и по часовой стрелке, и против неё, горизонтальный катет становится горизонтальным и наоборот. Кроме того, одно из приращений меняет знак. Таким образом, тангенс угла наклона прямой, перпендикулярной к y = k∙x, равен
Решение. Прямая y = k∙x проходит через начало координат и через точку (1; k). С этими двумя точками связан прямоугольный треугольник, катеты которого являются приращениями ∆х = 1 (горизонтальный катет) и ∆у = k (вертикальный катет). При повороте данного треугольника на 90° и по часовой стрелке, и против неё, горизонтальный катет становится горизонтальным и наоборот. Кроме того, одно из приращений меняет знак. Таким образом, тангенс угла наклона прямой, перпендикулярной к y = k∙x, равен  .
. , или после преобразований – уравнение
, или после преобразований – уравнение  .
.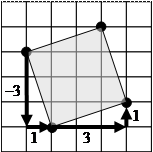 Задача 7. На плоскости заданы точки А (х1; у1) и В (х2; у2). Найти координаты точек С (х3; у3) и D (х4; у4), которые являются вершинами квадрата АВСD. Вычислить площадь этого квадрата.
Задача 7. На плоскости заданы точки А (х1; у1) и В (х2; у2). Найти координаты точек С (х3; у3) и D (х4; у4), которые являются вершинами квадрата АВСD. Вычислить площадь этого квадрата.