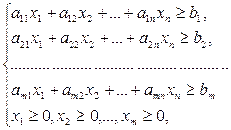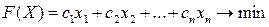|
|
Задача составления рациона (задача о диете, задача о смесях).Построение ЭММ задачи линейного программирования Задача линейного программирования – это такая задача, в которой определенное выражение (целевая функция) должно быть оптимизировано (максимизировано или минимизировано) при наличии ряда ограничений. Как целевую функцию, так и ограничения можно представить в виде линейных выражений. Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта. Построение ЭММ задачи линейного программирования включает в себя следующие основные моменты: 1. Определение переменных, которые будут использоваться. 2. Определение выражения целевой функции с учетом переменных. 3. Определение ограничений. Задача линейного программирования включает в себя оптимизацию целевой функции при наличии ряда ограничений. Рассмотрим примеры преобразования задач коммерческой деятельности к общей задаче линейного программирования и построения экономико-математических моделей. 1. Задача об использовании ресурсов (задача планирования производства). Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3 и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.
Прибыль, получаемая от единицы продукции P1 и P2, ‑ соответственно 2 и 3 руб. Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной. Решение. Составим экономико-математическую модель задачи. Обозначим x1, x2 – число единиц продукции соответственно P1 и P2, запланированных к производству. Для их изготовления по данным таблицы потребуется (
По смыслу задачи переменные Суммарная прибыль F составит 2х1 руб. от реализации продукции P1 и 3х2 руб. – от реализации продукции P2, т.е.
Требуется найти такой план выпуска продукции X=(x1, x2), удовлетворяющий системе ограничений (1.1) и условию (1.2), при котором функция (1.3) принимает максимальное значение. Обобщим задачу на случай выпуска n видов продукции с использованием m видов ресурсов. Обозначим xj (j=1, 2, …, n) – число единиц продукции Pj, запланированной к производству; bi (i=1, 2, …, m) – запас ресурса Si, aij – число единиц ресурса Si, затрачиваемого на изготовление единицы продукции Pj (числа aij часто называют технологическими коэффициентами); сj – прибыль от реализации единицы продукции Pj. Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид: найти такой план X=(x1, x2,…,xn) выпуска продукции, удовлетворяющий системе
при котором целевая функция принимает максимальное значение
Задача составления рациона (задача о диете, задача о смесях). Имеется два вида корма I и II, содержащие питательные вещества (витамины) S1, S2, и S3. Содержание числа единиц питательных веществ в 1 кг. Каждого вида корма и необходимый минимум питательных веществ приведен в таблице.
Стоимость 1 кг. корма I и II соответственно равна 4 и 6 руб. Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела. Решение. Составим экономико-математическую модель задачи. Обозначим x1, x2 – количество кормов I и II, входящих в дневной рацион. Тогда этот рацион будет включать (
Общая стоимость рациона составит (в руб.) Итак, экономико-математическая модель задачи: составить дневной рацион X=(x1, x2), удовлетворяющий системе ограничений (2.1), при котором функция (2.2) принимает минимальное значение. Для формулировки задачи в общей постановке обозначим: xj (j=1, 2, …, n) – число единиц корма m-го вида; bi (i=1, 2, …, m) – необходимый минимум содержания в рационе питательного вещества Si, aij – число единиц питательного вещества Si в единице корма j-го вида; сj – стоимость единицы корма j-го вида. Тогда экономико-математическая модель задачи примет вид: найти такой рацион X=(x1, x2,…,xn), удовлетворяющий системе
при котором целевая функция принимает минимальное значение
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
) единиц ресурса S1, ( 
) единиц ресурса S2, (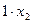 
) единиц ресурса S3 и 
единиц ресурса S4. Так как потребление ресурсов S1, S2, S3 и S4 не должно превышать их запасов, соответственно 18,15, 5 и 21 единицы, то связь между потреблением ресурсов и их запасами выразиться системой неравенств:
(1.1)
(1.2)
(1.3)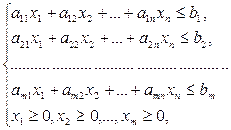
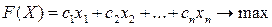
) единиц питательного вещества S1, ( 
)питательного вещества S2 и ( 
) единиц питательного вещества S3. Так как содержание питательных веществ S1, S2, и S3 в рационе должно быть не менее соответственно 9, 8, и 12 единиц, то получим систему неравенств:
(2.1)
. (2.2)
