
|
|
Задачи линейного программирования
Мы уже знаем о самых простых задачах. где выбор показателя эффективности (целевой функции) W достаточно явно диктуется целевой направленностью операции, а ее условия известны заранее (детерминированный случай). Тогда показатель эффективности зависит только от двух групп параметров: заданных условий я и элементов решения х, т. е. W = W ( a , as ). Напомним, что в числе заданных условий а фигурируют и ограничения, налагаемые на элементы решения. Пусть решение х представляет собой совокупность п элементов решения х1 , х2, ..., х n (иначе — n -мерный вектор):
Требуется найти такие значения х1 x 2 , ..., х n которые обращают величину W в максимум или в минимум (оба слова в математике объединяются под одним термином «экстремум»). Такие задачи — отыскания значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, носят общее название задач математического программирования. Трудности, возникающие при решении задач математического программирования, зависят: а) от вида функциональной зависимости, связывающей W с элементами решения, б) от «размерности» задачи, т. е. от количества элементов решения x 1 , x 2 , ..., xn , и в) от вида и количества ограничений, наложенных на элементы решения. Среди задач математического программирования самыми простыми (и лучше всего изученными) являются так называемые задачи линейного программирования. Характерно для них то, что: а) показатель эффективности (целевая функция) W линейно зависит от элементов решения x 1 t x 2 ..... xn и б) ограничения, налагаемые на элементы решения, имеют ннд линейных равенств или неравенств относительно x 1, x 2 , .. ., xn . Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д. Это и естественно, так как во многих задачах практики «расходы» и «доходы» линейно зависят от количества закупленных или утилизированных средств (например, суммарная стоимость партии товаров линейно зависит от количества закупленных единиц; оплата перевозок производите)! пропорционально весам перевозимых грузов н т. д.). Разумеется, нельзя считать, что все встречающиеся на практике типы зависимостей линейны; можно ограничиться более скромным утверждением, что линейные (и близкие к линейным) значимости встречаются часто, а это уже много значит.
Приведем несколько примеров задач линейного программирования. 1. Задача о пищевом рационе. Ферма производит откорм скота с коммерческой целью. Для простоты допустим, что имеется всего четыре вида продуктов: П1, II 2, П3, П4; стоимость единицы каждого продукта равна соответственно с1, с2, с3, c 4 Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков — не менее Ь\ единиц; углеводов — не менее Ь 2 единиц; жиров — не менее Ь 3 единиц. Для продуктов П1, П2, П3, П4 содержание белков, углеводов и жиров (в единицах на единицу продукта) известно и задано в таблице 7:1 , где aij ( i = l , 2, 3, 4; j = 1, 2, 3) — какие-то определенные числа; первый индекс указывает номер продукта, второй — номер элемента (белки, углеводы, жиры)'). Требуется составить такой пищевой рацион (т. в. назначить количества продуктов П1, П2, П3, П4, входящих в пего), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.
Составим математическую модель (в данном случае это очень просто). Обозначим х1, х2 , х3, х4 количества продуктов П1, П2, П3, П4, входящих в рацион. Показатель эффективности, который требуется минимизировать,— стоимость рациона (обозначим ее L ); она линейно зависит от х1,х2,х3, х4 L = с1х1 + с2х2 + с3х3 + с4х4 или, короче,
Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице продукта П1 содержится а11 единиц белка, в х1 единицах — а1х1, единиц белка, в х2 единицах продукта С2 содержится а21х2 единиц белка и т. д., получим три неравенства:
« iA + « iA + « sA + ««X» > К « w * i + «»А + « jA + а а х А > b,. Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х1 x 2 x 3 x 4. Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х1 , х2 , х3, х4 , чтобы они удовлетворяли ограничениям — неравенствам (7.3) и одновременно обращали в минимум линейную функцию этих переменных;
Перед нами — типичная задача линейного программирования. Не останавливаясь покуда на способах ее решения, приведем еще три примера аналогичных задач. 2. Задача о планировании производства. Предприятие производит изделия трех видан: U 1, U 2, U 3. По каждому виду изделия предприятию спущен план, по которому оно обязано выпустить м« менее Ь1единиц изделия U 1, не менее Ь2 единиц изделия U 2 и не менее b 2, единиц изделия U 3. План может быть не перевыполнен, но в определенных границах; условия спроса ограничивают количества произведенных единиц каждого типа: не более соответственно B 1, B 2, B 3 единиц. На изготовление изделий идет какое-то сырье; всего имеется четыре вида сырья: S 1 S 2 S 3 S 4, причем запасы ограничены числами Y 1 Y 2 , Y 3 , Y 4 единиц каждого вида сырья. Теперь надо указать, какое количество сырья каждого вида идет на изготовление каждого вида изделий. Обозначим au количество единиц сырья вида s , ( i = 1, 2, 3, 4), потребное на изготовление одной единицы изделия U , ( i =1, 2, 3). Первый индекс у числа а„ — вид изделия, второй — вид сырья. Значения a ti г ведены в таблицу (матрицу) При реализации одно изделие U 1 приносит предприятию прибыль c 1,U 2 — прибыль с 2 , U 3 — прибыль c 3. Требуется так спланировать производство (сколько каких изделий производить), чтобы план был выполнен или перевыполнен (но при отсутствии «затоваривания»), а суммарная прибыль обращалась в максимум Запишем задачу в форме задачи линейного программирования. Элементами решения будут х1, х 2 , хn — количества единиц изделий U 1, U 2, U 3, которые мы произведем. Обязательность выполнения планового задания запишется в виде трех ограничений-неравенств:
Отсутствие излишней продукции (затоваривания) даст нам еще три ограничения-неравенства:
Кроме того, нам должно хватить сырья. Соответственно четырем видам сырья будем иметь четыре ограничения-неравенства:
Прибыль, приносимая планом (х1, х2, х3), будет равна
Таким образом, мы снова получили задачу линейного программирования: найти (подобрать) такие неотрицательные значения переменных x 1 , x 2, x 3, чтобы они удовлетворяли неравенствам-ограничениям (7.4), (7.5), (7.6) и, вместе с тем, обращали в максимум линейную функцию этих переменных:
Задача очень похожа на предыдущую, разница в том, что неравенств-ограничений здесь больше и вместо «минимума» стоит «максимум» (а мы уже знаем, что это несущественно). В следующей задаче мы уже встретимся с другого вида ограничениями. 3. Задача о загруаке оборудования. Ткацкая фабрика располагает двумя видами ставков, из них N1 станков типа 1 иN2 станков типа 2. Станки могут производить три вида тканей: T 1, T 2, T 3 , но с разной производительностью. Данные a ( J производительности станков даны в таблице 7.3 (первый индекс — тип станка, второй — вид ткани). Каждый метр ткани вида Ti приносит фабрике доход c 1, вида Т2 — доход с2, Т3 — доход с3. Фабрике предписан план, согласно которому она должна производить в месяц не менее b 1 метров ткани T 1, Ь2 метров ткани Т2, Ь3 метров ткани T 3 3 ;
На первый (легкомысленный) взгляд поставленная адрес задача — родная сестра предыдущей. Рука так и тянется обозначить x lt x 2 , х n количества тканей T 1 t l ' i , Тз в плане н максимизировать суммарный доход c 1 x 1+ c 2 x 2+ c 3 x 3 . Но не торопитесь и спросите себя: а где же тут возможности оборудования? Поразмыслив, мы увидим, что в этой задаче элементы решения — не количества тканей каждого вида, а количества станков типов 1 н 2, занятых производством тканей ни ж дого вида. Здесь удобно обозначить элементы решения буквами х с двумя индексами (первый — тип станка, второй — вид ткани). Всего будет шесть элементов решения:
Здесь x 11 — количество станков типа 1, занятых изготовлением ткани T 1, x 12 — количество станков типа 1, занятых изготовлением ткани Т2, н т. д. Перед нами — еще одна задача линейного программирования. Запишем сначала условия-ограничения, наложенные на элементы решения хi .Прежде всего обеспечим выполнение плана. Это даст нам три неравенства - ограничения:
После этого ограничим перевыполнение плана; это даст нам еще три неравенства-ограничения:
Теперь запишем суммарный доход от производства всех видов тканей. Суммарное количество метров ткани Т\, произведенное всеми станками, будет равно a 11 x 11+ a 21 x 21 и принесет доход c 1( a 11 x 11+ a 21 x 21). Рассуждая аналогично, найдем суммарный доход фабрики за месяц при плане или, гораздо короче,
Перед нами — опять задача линейного программирования: найти такие неотрицательные значения переменных x 11 , x 12 , ..., x 23, которые, во-первых, удовлетворяли бы ограничениям-неравенствам (7.10), (7.11), во-вторых — ограничениям-равенствам (7.12) и, наконец, обращали бы в максимум линейную функцию этих переменных (7.13). В этой задаче линейного программирования шесть ограничений-неравенств и два ограничения-равенства.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 элементов решения
элементов решения




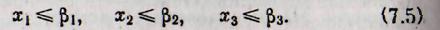



 количество метров каждого метра ткани не должно превышать соответственно B 1, B 2, B 3 метров. Кроме того, все без исключения станин должны быть загружены. Требуется так распределить загрузку станков производством тканей Т1, Т2, Т3,чтобы суммарный месячный доход был максимален.
количество метров каждого метра ткани не должно превышать соответственно B 1, B 2, B 3 метров. Кроме того, все без исключения станин должны быть загружены. Требуется так распределить загрузку станков производством тканей Т1, Т2, Т3,чтобы суммарный месячный доход был максимален.

 Теперь запишем ограничения, связанные с наличием оборудования и его полной загрузкой. Суммарное количество станков типа 1, занятых изготовлением всех тканей, должно быть равно Л N1; типа 2 — N 2 - Отсюда еще два условия — на этот раз равенства:
Теперь запишем ограничения, связанные с наличием оборудования и его полной загрузкой. Суммарное количество станков типа 1, занятых изготовлением всех тканей, должно быть равно Л N1; типа 2 — N 2 - Отсюда еще два условия — на этот раз равенства: 

 Эту линейную функцию шести аргументов мы хотим обратить в максимум:
Эту линейную функцию шести аргументов мы хотим обратить в максимум: .
.