
|
|
Основные операторы квантовой механики12 4.1. Оператор кинетической энергии, В классической механике кинетическая энергия дается выражением:
По принципу соответствия в квантовой механике ей соответствует оператор кинетической энергии: причем
4.2. Оператор полной энергии, В классической механике полная энергия выражается функцией Гамильтона:
где Т - кинетическая энергия, а U - потенциальная энергия. В квантовой механике функции Гамильтона соответствует оператор полной энергии, или гамильтониан. Оператор кинетической энергии дается выражением (1.36). Поскольку U(x,y,z) является функцией только координат, то по принципу соответствия оператор потенциальной энергии есть оператор умножения U(x,y,z) на соответствующую функцию. Иначе говоря,
4.3. Оператор момента импульса микрочастицы. Момент импульса частицы М в классической механике определяется как векторное произведение радиус-вектора
Проекции момента импульса на координационные оси можно представить в следующем виде:
Здесь x,y,z - координаты; px,py,pz - проекции импульса на соответствующие координатные оси. Полный момент импульса можно выразить через его составляющие следующим образом:
В квантовой механике моменту импульса соответствует оператор момента импульса,
где Применяя принцип соответствия, получим операторы проекций момента импульса:
Для оператора квадрата момента импульса (или "полного момента импульса") имеем
Важно отметить, что операторы проекций момента импульса на координатные оси свойством коммутативности не обладают, поскольку
однако они коммутируют с оператором квадрата момента импульса, т.е.
Свойства коммутативности в квантовой механике имеют большое значение. Так, если два оператора коммутируют, то можно определить собственные функции одного из них, зная собственные функции другого оператора. 4.4. Операторы спинового момента. Согласно экспериментальным данным для многих микрочастиц характерно наличие собственных механических моментов импульса. Собственный механический момент частицы принято называть спином частицы. В классической механике аналога спина нет. По аналогии с операторами момента импульса Пусть a - собственная функция спина, соответствующая спиновому квантовому числу Тогда
Отношения коммутирования для операторов спина и операторов момента импульса аналогичны, т.е.
Принимая во внимание выражения (1.44) и полученные коммутационные соотношения, мы допишем операторные уравнения для операторов проекций момента импульса:
Убедимся, что сделанный выбор операторов верен. Действительно, если подставить выражения (1.43) и (1.45) в выражение (1.44), получим сумму тождеств. Проверим это на примере первого коммутационного соотношения.
Подействуем оператором
Пусть Тогда
Аналогичные подстановки для второго и третьего из соотношений (1.44) также приводят к тождествам.
Элементы теории групп 1.5.1. Понятие о группе (симметрии) Из эксперимента известно, что большинство химических молекул обладают высокой симметрией, а изолированные атомы – сферической симметрией. Хотя часто нельзя получить точное решение уравнения Шредингера, можно получить некоторые представления о его виде, рассматривая свойства симметрии волновых функций. Очевидно, что волновая функция должна обладать теми же свойствами симметрии, что и молекула или атом, которые она описывает; последнее является следствием инвариантности энергии относительно преобразований симметрии. В частности, симметрию можно использовать для классификации волновых функций. Наиболее полезна для изучения симметрии теория групп. Остановимся на некоторых ее компонентах. Набор объектов (например, операторов) образует группу, если они удовлетворяют следующим условиям: (1) Если элементы (2) Для трех элементов (3) Для любого элемента (4) Единичный элемент Для химических приближений важно заметить, что операции симметрии молекул образуют группу. Рассмотрим для примера точки 1, 2, 3, 4 на осях координат (в этих точках могут располагаться, например, одинаковые атомы).
Расположение этих точек обладает высокой симметрией. Применение операций симметрии оставляет без изменения все или некоторые из этих точек. Взаимные переходы точек при операциях симметрии можно отобразить несколькими способами. (1) При помощи матриц. Положим, что матричный элемент aij = 1, если точка j переходит под действием операции симметрии в точку i, и aij = 0, если этого не происходит. Пусть Е – элемент идентичности; С4h – вращение на 90° в плоскости, перпендикулярной плоскости xОy; С2V(x) – поворот на 180° вокруг оси Ох; Сi – отражение в центре координат. Тогда
(2) При помощи перестановок.
Вообще говоря, существует бесконечное множество способов такого отображения. Однако все они обладают общим свойством: подчиняются групповым постулатам (1) - (4), и, следовательно, образуют группу. Набор матриц, характеризующий описанные выше переходы точек (объектов) при преобразованиях симметрии, называют представлением группы. Точки (объекты), на которые они действуют – базисными функциями представления. Выберем в качестве "базисных функций" 8 точек:
Теперь размерность матриц, представляющих операции симметрии в этой системе, будет 8 х 8. Но эти матрицы будут удовлетворять тем же правилам умножения, что и описанные ранее. Заметим, что не найдется операции симметрии, результатом действия которой было бы смешение точек 1-4 и 5-8. Матрицы полученного представления можно представить в виде двух блоков.
Иначе говоря, все эти матрицы можно представить в виде
причем М1 действует только на точки 1-4, а М2 – только на 5-8. Более того, по виду блоки М1 и М2 будут теми же. С точки зрения математики, такое разбиение матриц большей размерности на блочные матрицы с блоками меньшей размерности называется редукцией или приведением. Обычно представление обозначают греческой буквой Вместо точек можно было бы взять какие-то функции, например, волновые функции одинаковых атомов. Полученные результаты будут теми же. Указанные функции также будут базисными функциями. Важно заметить, что и точки и функции одной и той же симметрии будут образовывать базисные наборы для представления групп симметрии. Зададимся вопросом: можно ли еще более упростить (привести) матрицу размерности 4 х 4? Рассмотрим комбинации (Р1+Р2+Р3+Р4), (Р1+Р3-Р2-Р4), (Р3-Р1) и (Р4+Р2). Можно заметить, что при действии операций симметрии первые две суммы остаются неизменными или просто умножаются на –1 (симметрия и антисимметрия). Третья и четвертая комбинации смешиваются, но только друг с другом. Таким образом, они образуют базис для 3-х представлений, первые две – для одномерных
Дальнейшее разложение или редукция для Согласно Малликену существуют следующие правила для обозначения неприводимых представлений. (1) Размерность представления отображается в его имени: А или В – одномерные представления; Е – двухмерное представление; Т – трехмерное представление; U – четырехмерное представление. (2) Буква А означает, что представление симметрично при операции вращения вокруг главной оси группы симметрии, а В – антисимметрично. (3) Если есть центр симметрии, то добавляется подстрочный индекс "g", если его нет – "u". (4) Индексы 1 и 2 для неприводимых представлений А и В соответствуют симметричному (1) и антисимметричному (2) поведению относительно оси С2, перпендикулярной главной оси, а при ее отсутствии -sV. (5) Надстрочные индексы ' и " указывают симметричное (') или антисимметричное (") неприводимое представление по отношению к sh. 1.5.2. Метод характеров неприводимых представлений. Для применения теории групп необходимо знать неприводимые представления, для которых волновые функции молекулы являются базисными функциями. Их можно определить из таблиц характеров неприводимых представлений, известных из теории групп. Можно доказать, что для определения неприводимых представлений группы достаточно знать след (равный сумме диагональных элементов) матриц, представляющих операции симметрии. В теории групп след матриц представлений часто называют характером. Для всех представлений и операций группы они сведены в таблицу характеров. Пример одной из наиболее часто употребляемых групп, С2v, приведен ниже.
Такие таблицы составлены для всех точечных групп и будут в рамках данного курса использоваться без вывода. В этих таблицах +1 означает симметричность (неизменность) свойства функций базисного набора представления при осуществлении операции симметрии, а –1 – антисимметричность. Операции антисимметрии преобразуют предметы, обладающие двумя возможными значениями какого-либо свойства, так, что одно значение переходит в другое. Пример: знак функции. Важным свойством характеров неприводимых представлений является то, что таблица их умножения соответствует таблице умножения групп. Ниже приведены таблицы характеров наиболее часто встречающихся групп симметрии.
В теории групп вводится еще одно полезное для химии понятие: понятие о прямом произведении. Пусть Г1 – n1-мерное, а Г2 – n2-мерное представления группы G. Тогда матрицы размера (n1·n2) x (n1·n2), получаемые как прямые произведения матриц из Г1 и Г2, образуют n1·n2-мерное представление группы G, так называемое прямое (кронекеровское) произведение Прямое произведение
размера m·m' x n·n', где индекс j означает порядковый номер пары (i,i') в последовательности (1,1), (1,2), … , (1,m'), (2,1), (2,2), … , (m,m'), а индекс h – порядковый номер пары (k,k') в аналогичной последовательности. Характер
В качестве примера рассмотрим прямые произведения характеров неприводимых представлений в группе С3v.
Для того, чтобы закончить с описанием начал теории представлений, покажем два полезных приема: определение состава приводимого представления (разложения его на неприводимые) и использование операторов проектирования. Разложение приводимого представления на неприводимые. Можно показать, что разложение любого приводимого представления осуществляется единственным образом, причем число вхождений неприводимого представления i в приводимое представление Г, определяется по формуле:
Здесь ai –сколько раз i-ое неприводимое представление встречается в приводимом представлении, h – число элементов группы G; R – оператор симметрии группы; Характер приводимого представления в точечной группе определяется как число элементов базисного набора (представления) группы, которые остаются неподвижными при операции симметрии. Рассмотрим систему точек 1 … 4.
Тогда
Отсюда, структуру приводимого представления можно записать как
Последняя запись означает, что в базисный набор функций приводимого представления входят 3 функции, преобразующиеся по представлению А1 и одна – по представлению В1. Часто при применении теории групп для решения физических и химических задач используют метод операторов проектирования. Он позволяет преобразовать произвольный базис таким образом, чтобы он принадлежал к определенному неприводимому представлению группы симметрии. По определению, базис имеет вид:
Здесь h – число элементов симметрии в группе; i – неприводимое представление группы; Пусть ji – волновая функция атома в точке i:
Рис.2
Тогда волновые функции системы атомов 1-4, удовлетворяющие группе С2V, будут находиться следующим образом. Представление А1:
Таким образом y4 = y2, т.е. всего образовано 3 волновых функции, преобразующиеся по представлению А1 группы С2V. Представление В1.
1.5.3. Точечные группы симметрии молекул. Что означает симметрия объекта? По-видимому, можно сказать, что, если одна из конфигураций объекта при помощи поворотов вокруг определенных осей и отражений в определенных плоскостях (т.е. посредством операций симметрии) может быть приведена к другой конфигурации, неотличимой от исходной, то объект симметричен относительно этих операций. Операцией симметрии называется такое преобразование, которое приводит объект к новой его конфигурации, неотличимой и совмещаемой с исходной. Существуют лишь 5 элементов и операций симметрии (по крайней мере в случае конечных точечных групп). 1. Ось симметрии º (поворотная ось симметрии). Если поворот молекулы вокруг какой-либо оси на угол j (операция симметрии) приводит к новой конфигурации молекулы, не отличающейся от исходной, то такая ось называется осью вращения (элемент симметрии) порядка 2. Инверсия или отражение в центре инверсии. Если прямая линия, проведенная от любого атома через центр молекулы и продолженная в том же направлении, встретит на таком же расстоянии от центра молекулы эквивалентный атом, то молекула обладает центром симметрии. Центр симметрии обозначают буквой "i". 3. Отражение в плоскости симметрии (зеркальная плоскость). Если молекулу мысленно можно разделить пополам плоскостью так, что каждый атом из одной половины молекулы при отражении в этой плоскости переходит в подобный ему атом из другой половины молекулы (операция симметрии), то говорят, что молекула обладает зеркальной плоскостью. В зависимости от взаимного положения плоскостей и осей симметрии различают три случая. Если главная ось симметрии (º поворотная ось симметрии наивысшего порядка) перпендикулярна плоскости симметрии, то плоскость симметрии носит название горизонтальной плоскости симметрии и обозначается sh. Если главная ось симметрии параллельна (или содержится в) плоскости симметрии, то такая плоскость симметрии носит название вертикальной плоскости симметрии и обозначается sv. Если плоскость симметрии проходит через главную ось молекулы и делит пополам угол между двумя осями второго порядка, то она называется диагональной плоскостью симметрии и обозначается sd. 4. Зеркально-поворотная ось. Если молекула сначала поворачивается вокруг оси, и возникающая при этом конфигурация отражается в плоскости этой оси, и, если возникающая в конфигурация совпадает при наложении с исходной, то говорят, что молекула обладает зеркально-поворотной осью Sn порядка 5. Поворотно-инверсионная ось. Если молекула сначала поворачивается вокруг оси на угол j и с возникающей при этом конфигурацией молекулы проводится инверсия и, если возникающая конфигурация совпадает при положении с исходной, то эта операция называется поворотом с инверсией Совокупность перечисленных элементов симметрии образует точечную группу. По определению, точечной группой симметрии называется такая группа, при выполнении любой операции симметрии по крайней мере одна точка пространства остается неизменной.
1.5.4. Правила отнесения молекул к точечным группам симметрии (по Орчину и Джаффе). 1. Находим поворотную ось наивысшего порядка. Если эта ось имеет бесконечный порядок, т.е. молекула линейна, то она принадлежит к точечным группам 2. Если наивысшая поворотная ось является осью 3-го, 4-го или 5-го порядка, то следует искать другие оси того же порядка. (а) Если имеется несколько осей 5-го порядка, то молекула принадлежит к группе (б) Если имеются 3 поворотные оси 4-го порядка, то молекула принадлежит к группе (в) Если имеются 4 оси 3-го порядка, то возможны три случая: (а) если нет центра инверсии – группа (б) если есть центр инверсии – группа (в) если есть 6 плоскостей и 3 зеркально-поворотные оси 4-го порядка – группа 3. Если только одна ось имеет порядок n больше двух или, если наивысшая поворотная ось является осью 2-го порядка, то нужно проверить, есть ли у молекулы еще n-осей второго порядка, расположенных под прямым углом друг к другу. (а) Если эти оси существуют, и, если у молекулы нет плоскости симметрии, то группа обозначается (б) Если есть горизонтальная плоскость, то группа - (в) Если имеется n вертикальных плоскостей, но ни одной горизонтальной, то пространственной группой будет 4. Если существует единственная поворотная ось n-го порядка, то необходимо искать ось (а) если нет плоскостей – группа (б) если имеется n вертикальных плоскостей – группа (в) если есть горизонтальная плоскость, то группа 5. Если нет никаких осей, то при наличии плоскости молекулу относят к группе при наличии центра инверсии – к при отсутствии каких-либо элементов симметрии – группа
//////////1.5.5. Применение теории групп в квантовой химии для оценки интегралов. 1.5.5. Применение теории групп в квантовой химии. 1. Фундаментальным свойством волновых функций является то, что они могут использоваться в качестве базиса неприводимых представлений точечных групп молекул. Это утверждение является следствием теоремы Вигнера, согласно которой собственные функции молекулярной системы принадлежат к одному из типов симметрии данной группы. Поэтому знание точечной группы симметрии молекулы позволяет определить многие из свойств волновой функции молекулы, а иногда и конкретный вид этой функции. 2. Симметрия волновой функции позволяет часто определить величины интегралов, включающих волновые функции. В математике существует теорема о том, что интеграл от какой-либо функции по всей области изменения ее аргументов равен нулю тогда и только тогда, когда ее подынтегральной выражение является нечетным. Например,
Четность подынтегрального выражения определяется типом неприводимого представления, базисной функцией которого оно является. Поэтому можно утверждать, что
если f(t) преобразуется по полностью симметричному неприводимому представлению теории групп. Рассмотрим два важных частных случая. (а) Интегралы перекрывания волновых функций
Поскольку Рассмотрим далее интегралы
Можно показать, что Действительно, оператор
Важное замечание. К сожалению, применение симметрии для оценки интегралов помогает лишь определить, когда интегралы будут точно равны нулю. Однако, если согласно теории групп интеграл отличен от нуля, он, тем не менее, может быть равен нулю. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.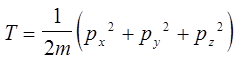

 , (1.36)
, (1.36) .
. ,
, (1.37)
(1.37) , проведенного от начала координат к частице, на импульс,
, проведенного от начала координат к частице, на импульс,  , т.е.
, т.е. .
.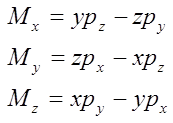
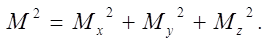
 (1.38)
(1.38) - векторный оператор импульса;
- векторный оператор импульса;  - радиус-вектор.
- радиус-вектор. (1.39)
(1.39) (1.40)
(1.40) (1.41)
(1.41) (1.42)
(1.42) Паули ввел операторы спина электрона
Паули ввел операторы спина электрона  .Чтобы данные теории соответствовали эксперименту необходимо предположить, что оператор
.Чтобы данные теории соответствовали эксперименту необходимо предположить, что оператор 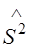 имеет только одно собственное значение
имеет только одно собственное значение  , а оператор
, а оператор  - два собственных значения
- два собственных значения  и
и  .
. , а b - спиновая собственная функция, соответствующая
, а b - спиновая собственная функция, соответствующая  .
. (1.43)
(1.43)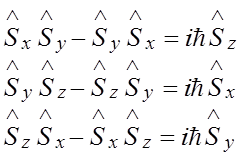 (1.44)
(1.44) (1.45)
(1.45)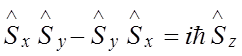
 на собственную функцию a.
на собственную функцию a.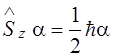
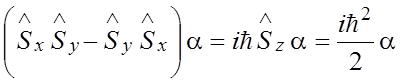
 .
.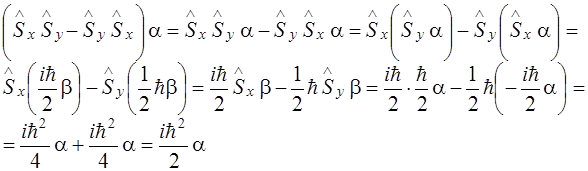
 и
и  принадлежат группе, то принадлежит группе и произведение
принадлежат группе, то принадлежит группе и произведение 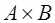 .
. , принадлежащих группе, справедлив ассоциативный закон умножения, т.е.
, принадлежащих группе, справедлив ассоциативный закон умножения, т.е.  .
. , который также принадлежит группе.
, который также принадлежит группе. также принадлежит группе.
также принадлежит группе.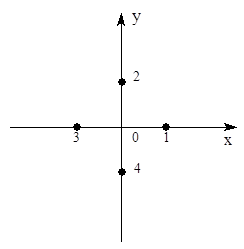
 ;
;  ;
;  ;
;  и т.п.
и т.п. ;
;  ;
;  ;
;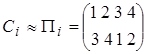 и т.п.
и т.п.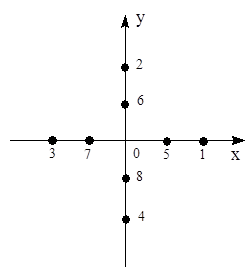
 ;
;  ;
;  ;
;  .
. ,
, . Описанная выше редукция будет иметь вид
. Описанная выше редукция будет иметь вид  .
. , две последних – для двухмерного
, две последних – для двухмерного  . Тогда
. Тогда
 невозможны; такие представления называются неприводимыми в отличие от исходных представлений
невозможны; такие представления называются неприводимыми в отличие от исходных представлений  , которые называются приводимыми.
, которые называются приводимыми. .
. матрицы
матрицы  размера m x n и матрицы
размера m x n и матрицы  размера m' x n' есть матрица
размера m' x n' есть матрица (1.46)
(1.46) представления
представления  равен произведению характера
равен произведению характера  представления
представления 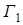 и характера
и характера  представления
представления  :
: (1.47)
(1.47)





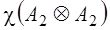
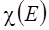 =
= 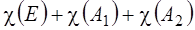

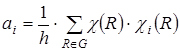 (1.48)
(1.48) - характер операции R в приводимом представлении;
- характер операции R в приводимом представлении;  - характер операции R в i-том неприводимом представлении.
- характер операции R в i-том неприводимом представлении.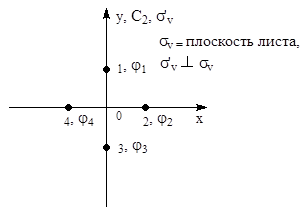

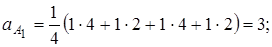
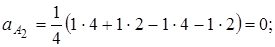
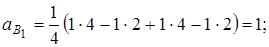
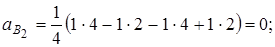
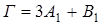
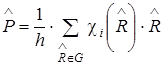
 - операция группы;
- операция группы; 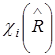 - характер операции
- характер операции 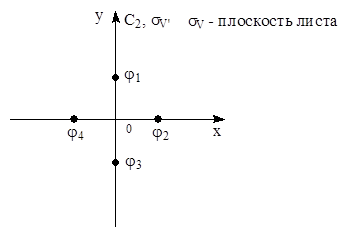
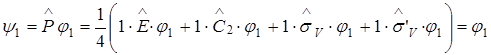
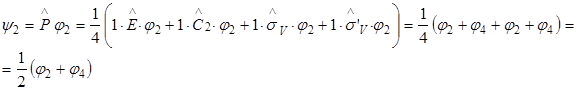
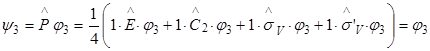
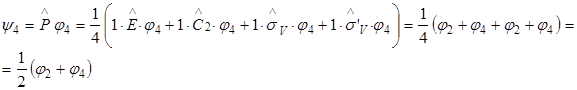
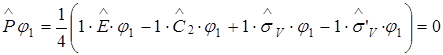
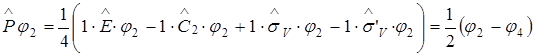
 и обозначается Cn.
и обозначается Cn. порядка
порядка  и
и  . Если молекула имеет центр инверсии, то она принадлежит к группе
. Если молекула имеет центр инверсии, то она принадлежит к группе  или
или  (в зависимости от того, есть ли у нее плоскости симметрии (
(в зависимости от того, есть ли у нее плоскости симметрии (  (есть плоскость симметрии) или
(есть плоскость симметрии) или  (плоскости симметрии нет).
(плоскости симметрии нет). ;
; ;
; .
. ;
; ;
; .
. . Если ось
. Если ось 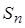 ; если оси
; если оси  ;
; ;
; .
. ;
; ;
; .
. , но
, но 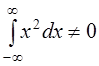

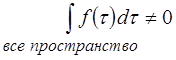 ,
,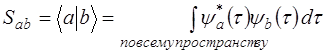
 тогда и только тогда, когда
тогда и только тогда, когда  преобразуется по полностью симметричному неприводимому представлению. Но последнее имеет место лишь, если
преобразуется по полностью симметричному неприводимому представлению. Но последнее имеет место лишь, если  и
и  преобразуются по одному и тому же неприводимому представлению (по теореме о прямом произведении).
преобразуются по одному и тому же неприводимому представлению (по теореме о прямом произведении).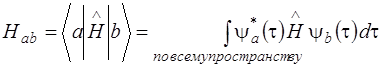
 , если
, если  всегда относится к полностью симметричному представлению. Следовательно, симметрия всего подынтегрального выражения будет определяться симметрией прямого произведения функций
всегда относится к полностью симметричному представлению. Следовательно, симметрия всего подынтегрального выражения будет определяться симметрией прямого произведения функций  и
и