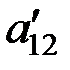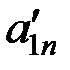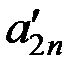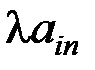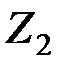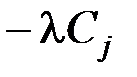|
|
Задачи линейного программированияПонятие линейного программирования. Линейное программирование – раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, её целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Методами ЗЛП могут решаться задачи: о наилучшем использовании ресурсов; о выборе оптимальных технологий; о размещении ремонтов специализированного оборудования; транспортная задача (задача развития электрических сетей); о размещении заказа и т.д. В перечисленных задачах может определяться или максимум или минимум целевой функции. Задача развития электрических сетей (транспортная задача). Модель транспортной задачи – транспортировка некоторого однородного продукта (электроэнергии) от производителей к потребителям, при этом должен иметься баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем потребителям безразлично, из каких пунктов производства будет поступать электроэнергия, лишь бы их заявки были полностью удовлетворены. Так как от схемы прикрепления потребителей к поставщикам существенно зависит объем передаваемой энергии, возникает задача о наиболее рациональной схеме электрических сетей (рациональное напряжение, количестве и сечений линий, трансформаций и др.), при котором потребности полностью удовлетворяются, все производство электроэнергии технологически обеспечивается, а затраты на проектирование сетей и передачу энергии потребителям минимальны. Задача формулируется так. Имеется m пунктов производства, в каждом из которых может быть произведено bi (i = 1,m) электроэнергии и n пунктов потребления электроэнергии, где потребность составляет aj (j = 1,n) единиц. Известны величины cij – затраты на транспортировку на единицу электроэнергии из i – го пункта в j – й пункт потребления. Обозначим через xij количество электроэнергии, передаваемого из i – го пункта производства в j – й пункт потребления. Матрица [cij] – называется матрицей тарифов, Х = [xij] – матрицей транспортировки. С целью удобства построения математической модели матрицы тарифов и транспортировки совмещают в одну, именуемую макетом транспортной задачи (развития сетей) (табл.5.1). Таблица 5.1 – Макет развития электрической сети
Математическая модель задачи развития электрической сети: целевая функция, описывающая транспортные затраты при ограничениях: на возможности производителя – весь продукт из пунктов производства может быть транспортирован
на спрос потребителей, который должен быть полностью удовлетворен:
при условии не отрицательности переменных, исключающем обратные перетоки
Основные виды записи ЗЛП. Общей задачей линейного программирования (ОЗЛП) называют задачу, которую математически представляют в виде следующих линейных соотношений: – целевая функция – W =
где – Сj , aij, bi – заданные действительные числа; xj ≥ 0 (j = 1,..,n) – искомые неотрицательные переменные параметры, удовлетворяющие условию задачи и ограничениям; Х = (Х1; ; Хп)t – план задачи. Канонической формой записи ЗЛП называют задачу
Каноническая форма записи ЗЛП может быть представлена в матричной форме и в векторной форме. Введем обозначения: A = где С – матрица-строка; А – матрица системы уравнений; Х – матрица – столбец переменных; А0 – матрица-столбец свободных членов. Каноническая форма задачи с использованием матричной записи примет вид
или min W = СХ, АХ = А0, Х ≥ 0.
Векторная форма записи ЗЛП. Для столбцов матрицы А введем обозначения: А1 = Тогда задача (5.7) – (5.9) в векторной форме записи примет вид: где cx – скалярное произведение векторов с=(с1;с2;...;сп) и х=(х1; х2;..; хп).
Геометрическая интерпретация задачи линейного планирования Геометрическая интерпретация задачи позволяет наглядно определить структуру, выявить особенности и открыть пути исследования более сложных свойств. Задачи линейного планирования с двумя переменными можно решить графически. В трехмерном пространстве графическое решение усложняется, а в n –мерном пространстве графическое решение невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства общей задачи линейного планирования, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации. Пусть дана задача: определить параметры Х1 ≥ 0, X2 ≥ 0, обеспечивающие максимум целевой функции и удовлетворяющие условиям ограничений
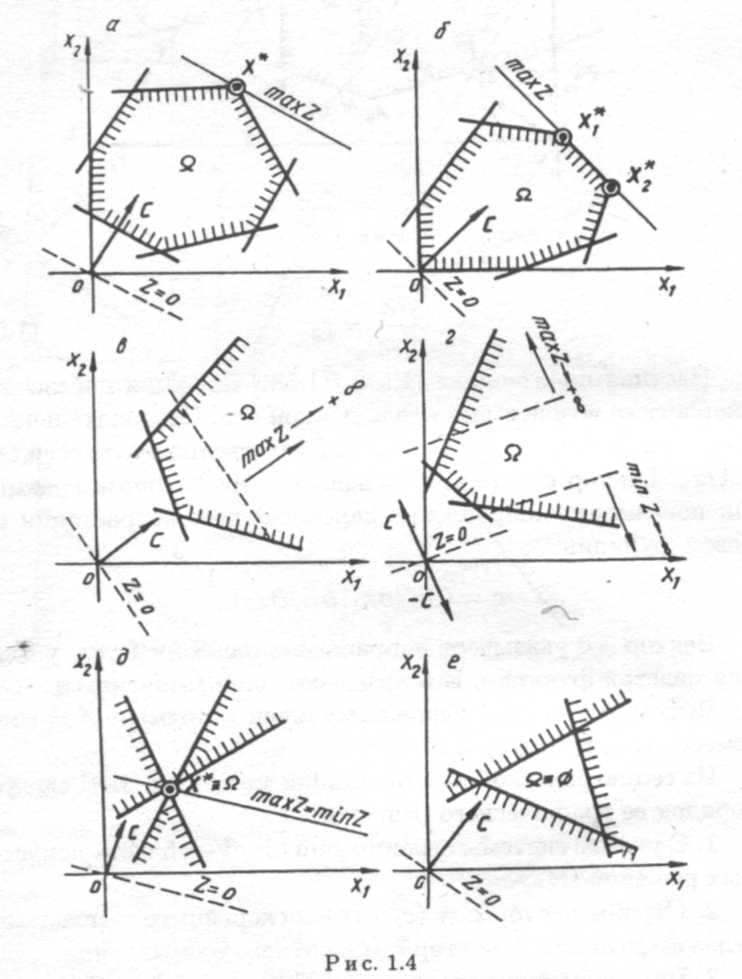
Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений (5.11) задаёт на плоскости х1Ох2 некоторую полуплоскость. Полуплоскость – выпуклое множество. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи (5.10) – (5.11) есть выпуклое множество. Представим на рис. 5.1 возможные ситуации, когда область допустимых решений (ОДР) задачи линейного планирования (ЗЛП): а) выпуклый многоугольник; б) неограниченная выпуклая многоугольная область; в) единственная точка; г) луч; д) отрезок; е) пустое множество.
Рис.5.1 Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП – непустое множество, например многоугольник АВСДЕ (рис.5.2). Выберем произвольное значение целевой функции Z = Zo. Получим с0 + с1х1 + с2х2 = Z0. Это уравнение прямой линии. В точках прямой MN целевая функция сохраняет одно и то же постоянное значение Z0. Считая в равенстве (5.10) Z параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения). Возникает вопрос: как установить направление возрастания (убывания) целевой функции? Найдём частные производные целевой функции по х1 и х2:
Частные производные (5.12) функции показывают скорость ее возрастания вдоль осей. Следовательно, с1 и с2 – скорость возрастания Z соответственно вдоль осей Ох1 и Ох2. Вектор G = (с1;с2) называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:
Вектор – G показывает направление наискорейшего убывания целевой функции. Его называют антиградиентом. Вектор Из геометрической интерпретации элементов ЗЛП следует порядок её графического решения. 1. С учетом системы ограничений строим область допустимых решений. 2. Строим вектор 3. Проводим произвольную линию уровня Z = Z0 (проще всего провести линию Z = c0, перпендикулярную к вектору G ). 4. При решении задачи на максимум перемещаем линию уровня Z = Z0 в направлении вектора G так, чтобы она касалась ОДР в её крайнем положении (крайней точке) (на рис.5.2 – до точки Д). В случае решения задачи на минимум линию уровня Z = Z0 перемещаем в направлении антиградиента (на рис. 5.2 – до точки В). 5. Определяем оптимальное решение, т.е. значения Х* = (х1*; х2*) и экстремальное значение целевой функции Z* = z( x*). Из геометрической интерпретации условий ограничений и целевой функции возможно выявить особенности решения ЗЛП, а именно (см. рис.5.3):
Рис.5.3 1) – оптимальное решение единственное: линия уровня и область допустимых решений в соответствующем положении имеют одну общую точку (рис.5.3, а); 2) – оптимальных решений бесконечное множество: в соответствующем положении линия уровня проходит через сторону области допустимых решений (рис.5.3, б); 3) – целевая функция не ограничена: линия уровня, сколько бы ее ни перемещали, не может занять соответствующего положения (рис.5.3, в,г); 4) – область допустимых решений состоит из единственной точки, где целевая функция достигает одновременно и максимального, и минимального значений (рис. 5.3, д); 5) – задача не имеет решения: область допустимых решений – пустое множество, т.е. система ограничений несовместна (рис.5.3 е). При количестве переменных более трех ЗЛП теряет геометрическую наглядность, но идея получения решения (графического) сохраняет смысл и для случая многомерного пространства. Переход к канонической форме. Как следует из общей задачи линейного планирования, в которой для целевой функции может определяться либо максимум, либо минимум, в них большинство ограничений задаются неравенствами. Наиболее же широко используемые методы решения задач линейного планирования применяются лишь к задачам, записанным в канонической форме. Поэтому приходится переходить от любой формы ЗЛП к ее каноническому виду, причем нужно быть уверенным, что эти формы эквивалентны. Пусть исходная ЗЛП имеет вид
Канонической формой записи ЗЛП называют задачу
При необходимости задачу максимизации можно заменить задачей минимизации, и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если Итак, То же самое имеет место и в случае функции многих переменных (n):
Преобразуем систему ограничений к каноническому виду. Введем m дополнительных неотрицательных переменных
Для того чтобы неравенства типа ≥ (5.15) преобразовать в равенства, из их левых частей вычтем дополнительные переменные
Дополнительные переменные
Задача (5.22) – (5.25) имеет каноническую форму. Задачи (5.13) –(5.16) и (5.22) – (5.25) тесно связаны между собой. Симплексный метод Для решения ЗЛП в аналитической форме применяют один из методов решения – симплекс метод (метод последовательного улучшения решения), который предполагает: 1) умение находить начальный опорный план; 2)наличие признака оптимальности плана; 3) умение переходить к не худшему опорному плану. Для построение начального опорного плана исходные данные задачи должны быть представлены в канонической форме. Пусть ЗЛП представлена системой ограничений в каноническом виде:
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при не отрицательности правой части (вi ≥ 0) левая часть ограничения содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения – равенства – с коэффициентом, равным нулю. Например, в системе ограничений x1 + 2x2 – 4x4 = 5, 2x2 + x3 + 2x4 = 8, x2 - 3x4 = 3 первое и второе ограничения имеют предпочтительный вид, третье –нет. Если каждое ограничение-равенство ЗЛП в каноническом виде содержит переменную, входящую в левую часть с коэффициентом, равным единице, а во все остальные с коэффициентом, равным нулю (при не отрицательности правых частей), то говорят, что система ограничений представлена в предпочтительном виде. В этом случае легко найти ее опорное решение (базисное с не отрицательными координатами): все свободные переменные нужно приравнять нулю, тогда базисные переменные (БП) будут равны свободным членам. Если полученный план будет иметь не более m отличных от нуля координат, то он будет опорным. Приравнивание предпочтительных переменных к правым частям дает базисное решение, т.е. крайнюю точку многоугольника. Поэтому предпочтительные – базисные. Переменные, приравниваемые нулю, - свободные. Пусть система ограничений имеет вид
Приведем систему к каноническому виду
которая имеет предпочтительный вид. Следовательно, начальный опорный план примет вид: Х0 = (0;0;……0; b1;b2; …….bm). В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю. Пусть система ограничений имеет вид
Приведем систему к каноническому виду
которая не имеет предпочтительный вид, так как дополнительные переменные xn+i входят в левую часть (при bi ≥ 0) с коэффициентом -1. Поэтому, базисный план Х0 = (0;0;...0; -b1; -b2;… -bm) является недопустимым. В практических задачах всегда имеются условия ограничений, которые в каноническом виде преобразуются из соотношений (5.18), поэтому можно перейти к улучшенному решению. Приведем последовательность шагов при решении задачи оптимизации: шаг первый: Приводим задачу к канонической форме Z = c0 – (
шаг второй: Находим начальный опорный план, приравняв шаг третий: Проверяем, оптимально ли найденное решение. Если решение оптимально, то вычисления окончены, в противном случае необходим переход к следующему опорному плану. Выполнение этого шаг требует анализа коэффициентов в функции цели при свободных переменных и проверки не отрицательности значений БП. Если значения БП удовлетворяют условию не отрицательности, то решение одно из допустимых (т.е. это одна из вершин ОДР). На оптимальность решения будут указывать отрицательные значения коэффициентов шаг четвертый: Переход к новой вершине ОДР, в которой значение целевой функции меньше начального. Наибольшее из положительных коэффициентов Приравнивают БП к нулю для всех ограничений на данном шаге. Находят отношения Все преобразования симплекс – метода можно выполнить в табличной форме. Табличная форма симплекс – метода предполагает представление исходной задачи в канонической форме (см. выше). Для внесения исходных данных в таблицу запишем условие задачи следующим образом:
Коэффициенты при свободных переменных в уравнениях БП и функции цели внесем в таблицу, причем разместим их в верхние части клеток со знаками, указанными в скобках соответствующих уравнений. Таблица 5.2
Столбец «свободные члены» определяет первое начальное решение при равенстве нулю свободных переменных: Z1( Далее выполняем шаги 3 и 4 симплекс - преобразований. Наибольший коэффициент при свободных переменных в функции цели определяет разрешающий столбец (пусть это будет хj). Находим наименьшее положительное отношение Дляпересчетакоэффициентов базисных переменных и функции цели через новые свободные переменные выполним следующее: 1) находим l = 1/аij; аij - генеральный элемент; 2) все коэффициенты разрешающей строки умножим на l (кроме генерального), а коэффициенты разрешающего столбца - на "-l" изапишем в нижней части клеток; 3) выделим старые значения коэффициентов разрешающей строки (┘) и новые значения коэффициентов разрешающего столбца (l); 4) числа, вводимые в нижнюю часть клетки на пересечении строки l и столбца S находим перемножением старого значения коэффициентов разрешающей строки и нового значения коэффициентов разрешающего столбца. После заполнения, всех клеток таблицы осуществляют ее преобразование в новую таблицу: Во все верхние отделения клеток разрешающей строки и разрешающего столбца заполняются значения из нижних отделений предыдущей таблицы; в остальные клетки помещают алгебраическую сумму значений данной клетки. Анализируя полученную таблицу, видим, что решение «улучшено», т.е. Z1 > Z2 . Далее выполняем действия, аналогичные вышеописанным. Таблица 5.3

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 min (5.1)
min (5.1)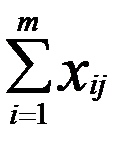 ≤ bi (i=1,…,m) (5.2)
≤ bi (i=1,…,m) (5.2) = ai (j=1,…,n) (5.3)
= ai (j=1,…,n) (5.3) (i = 1,..,m; j = 1,..,n) (5.4)
(i = 1,..,m; j = 1,..,n) (5.4) → max(min) (5.5)
→ max(min) (5.5) (5.6)
(5.6) (5.7)
(5.7) , i = (1,2, ,m ) (5.8)
, i = (1,2, ,m ) (5.8) (j = 1,…,n). (5.9)
(j = 1,…,n). (5.9)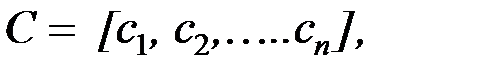
 , X =
, X = 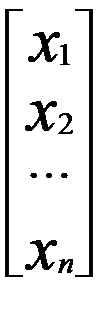 , A0 =
, A0 =  ,
, 
 =
= 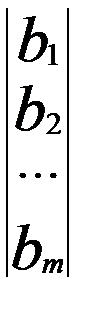 , X ≥0
, X ≥0  , А2 =
, А2 = 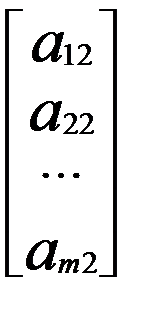 , А3 =
, А3 = 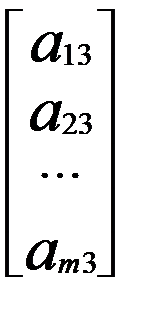 ,…, Аj =
,…, Аj =  ,…., Аn =
,…., Аn = 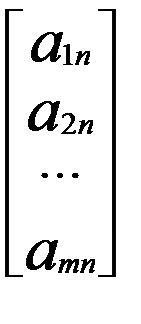 .
.
 x ≥ 0,
x ≥ 0, 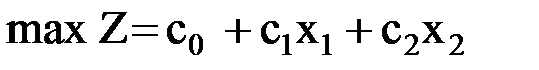 ; (5.10)
; (5.10)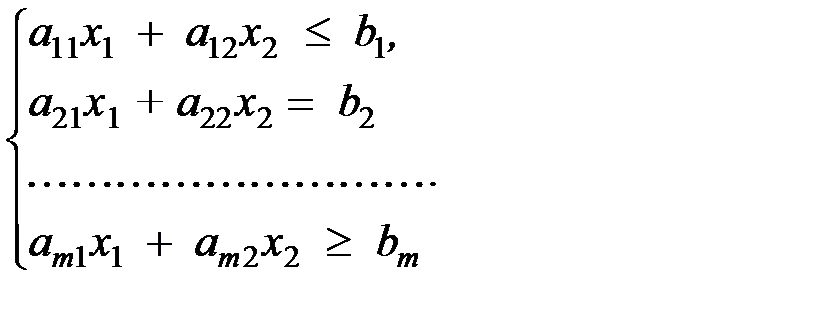 (5.11)
(5.11)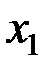
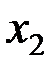


 ;
;  . (5.12)
. (5.12)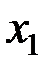
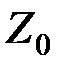



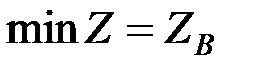
 .
.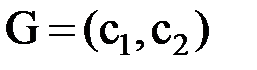 перпендикулярен к прямым Z = const семейства
перпендикулярен к прямым Z = const семейства  .
.
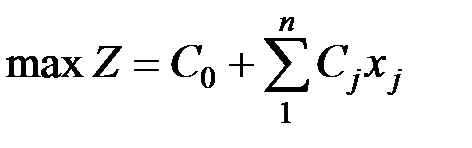 (5.13)
(5.13)
 (5.14)
(5.14)
 (5.15)
(5.15)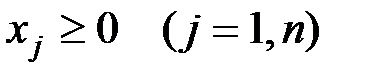 (5.16)
(5.16) (5.17)
(5.17)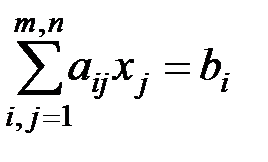 (5.18)
(5.18)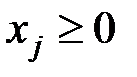 (j = 1,…,n). (5.19)
(j = 1,…,n). (5.19)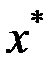 – точка максимума функции
– точка максимума функции  , то для функции
, то для функции 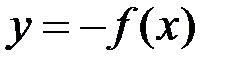 она является точкой минимума, так как графики функции
она является точкой минимума, так как графики функции  и
и  – симметричны относительно оси абсцисс (рис.5.4).
– симметричны относительно оси абсцисс (рис.5.4). .
. .
.


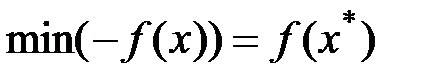


 . Для того чтобы неравенства типа ≤ (5.14) преобразовались в равенства, к их левым частям прибавим дополнительные переменные
. Для того чтобы неравенства типа ≤ (5.14) преобразовались в равенства, к их левым частям прибавим дополнительные переменные 
 , после чего система неравенств (5.14) примет вид:
, после чего система неравенств (5.14) примет вид: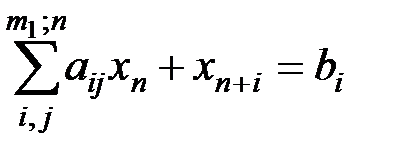 . (5.20)
. (5.20)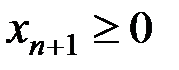
 . Получим
. Получим (5.21)
(5.21)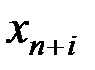
 в целевую функцию вводятся с коэффициентами, равными нулю. Целевую функцию умножаем на минус единицу. Получим задачу:
в целевую функцию вводятся с коэффициентами, равными нулю. Целевую функцию умножаем на минус единицу. Получим задачу: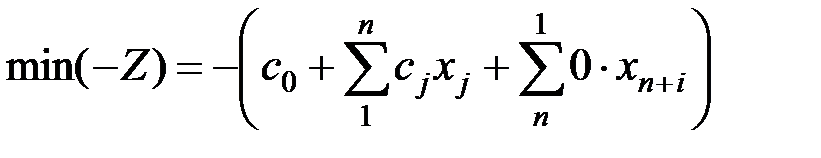 (5.22)
(5.22)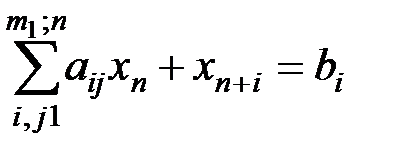 (5.23)
(5.23) (5.24)
(5.24)


 (5.25)
(5.25)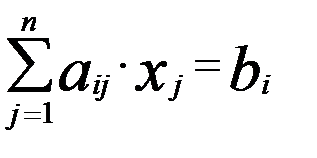 , bi ≥ 0 (i = 1, m).
, bi ≥ 0 (i = 1, m).  , bi ≥ 0 (i = 1, m).
, bi ≥ 0 (i = 1, m).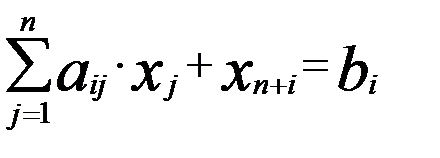 , bi ≥ 0 (i = 1, m),
, bi ≥ 0 (i = 1, m),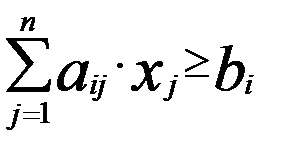 , bi ≥ 0 (i = 1,… m).
, bi ≥ 0 (i = 1,… m).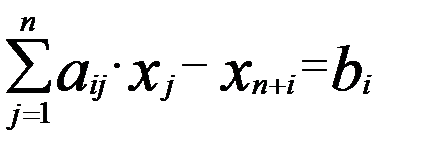 , bi ≥ 0 (i = 1,.. m),
, bi ≥ 0 (i = 1,.. m), ) → min;
) → min; – БП;
– БП;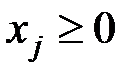 – свободные переменные.
– свободные переменные. , тогда Z = c0 ,
, тогда Z = c0 ,  .
.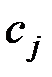 в целевой функции. В случае наличия положительных коэффициентов
в целевой функции. В случае наличия положительных коэффициентов  решение может быть улучшено.
решение может быть улучшено.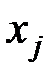 , которая может изменяться от нуля до значений, не нарушающих условия ограничений.
, которая может изменяться от нуля до значений, не нарушающих условия ограничений. для j – oй свободной переменной при условии равенства нулю других свободных переменных
для j – oй свободной переменной при условии равенства нулю других свободных переменных  . Наименьшее из положительных
. Наименьшее из положительных  укажет ту БП, которая станет свободной, т.е. укажет уравнение ограничений, из которого определится новая БП, выраженная через новые свободные переменные. Все остальные БП и функцию цели нужно пересчитать через новые свободные переменные. Т. о. будет получен очередной опорный план. Далее повторение шагов 3 и 4. Выполнение шагов один – четыре предполагает последовательные преобразования условий ограничений и функции цели. Поэтому, в дальнейшем будем говорить о решениях, полученных методом симплекс – преобразований.
укажет ту БП, которая станет свободной, т.е. укажет уравнение ограничений, из которого определится новая БП, выраженная через новые свободные переменные. Все остальные БП и функцию цели нужно пересчитать через новые свободные переменные. Т. о. будет получен очередной опорный план. Далее повторение шагов 3 и 4. Выполнение шагов один – четыре предполагает последовательные преобразования условий ограничений и функции цели. Поэтому, в дальнейшем будем говорить о решениях, полученных методом симплекс – преобразований. ) → min;
) → min; – БП;
– БП;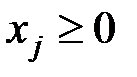 – свободные переменные.
– свободные переменные.






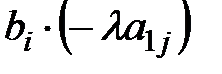
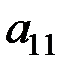
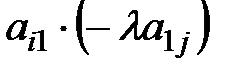



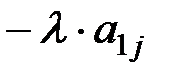

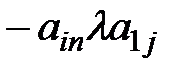








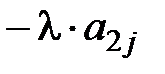

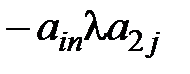









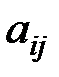
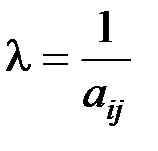
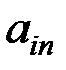








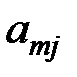

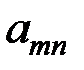
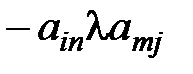
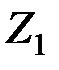
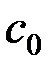



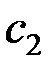

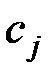



 )=c0 X
)=c0 X  .
.
 , которое определяет разрешающую строку. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, называют генеральным (обведем его кружком). Разрешающая строка показывает: какая базисная переменная поменяется со свободной переменной хi « xj .
, которое определяет разрешающую строку. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, называют генеральным (обведем его кружком). Разрешающая строка показывает: какая базисная переменная поменяется со свободной переменной хi « xj .