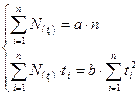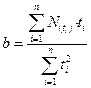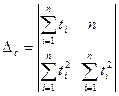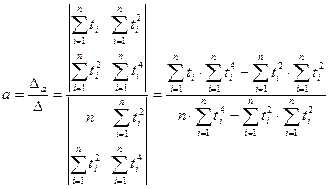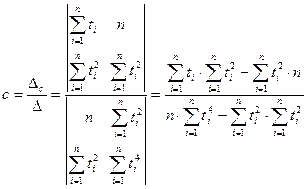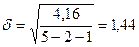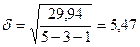|
|
Метод регрессионного анализаТранспортная логистика (в примерах и задачах)
Учебное пособие
Для специальности 24.01.00 «Организация перевозок и управление на транспорте (железнодорожном)»
Москва 2004 УДК 658.7 Л –
Лысенко Н.Е., Каширцева Т.И. Транспортная логистика (в примерах и задачах): Учебное пособие. — М.: МИИТ, 2004. ‑ 46с. Настоящее учебное пособие содержит методологические основы и примеры решения задач по курсу «Логистика», «Основы логистики» и «Транспортная логистика». Пособие предназначено для студентов, обучающихся по специальности «Организация перевозок и управление на транспорте (железнодорожном)», а также может быть использовано студентами других специальностей при выполнении практических занятий по указанным дисциплинам и выполнении работы. Ил.9, табл.8 прил.8, библиогр.8 назв. Рецензенты: Г.В. Бухало — к.т.н., доцент РГОТУПС А.В. Вакульчик — начальник службы грузовой и коммерческой работы Московской ж.д.
© Московский государственный университет путей сообщения (МИИТ), 2004 ВВЕДЕНИЕ В учебном пособии приведены методологические основы и примеры решения задач, наиболее часто решаемых в курсах «Логистика», «Основы логистики» и «Транспортная логистика». Приведенные задачи предлагаются для решения на практических занятиях по указанным дисциплинам. Для каждой задачи в пособии излагается методика решения в объеме, достаточном для ее выполнения и указывается литературный источник, из которого студенты могут пополнить и расширить свои знания по изучаемой теме. Ко всем задачам в пособии даны приложения, в которых приведены варианты исходных данных. Номера вариантов исходных данных задаются преподавателем, ведущим практические занятия. В пособии приведены примеры решения задач по определению размеров и прогнозированию материальных потоков, определению оптимального размера партии поставки, объемов работы и числа центров сервисного обслуживания, выбору места расположения сервисного центра (распределительного склада), определению границ рынка, равновесной цены, коэффициента эластичности, а также оптимизации распределения ресурсов между звеньями логистической транспортной цепи. Решение приведенного перечня задач позволит студентам закрепить теоретические знания и приобрести начальные навыки решения практических задач в изучаемой области науки. Учебное пособие рекомендуется для студентов, обучающихся по специальности «Организация перевозок и управление на транспорте (железнодорожном)», а также может быть использовано студентами других специальностей, изучающих основы логистики. Пособие издается нами впервые, и авторы будут весьма признательны читателям и пользователям за пожелания и замечания. Задача. Рассчитать величины входящего, выходящего, внешнего, внутреннего и суммарного материального потока для контейнерной площадки при следующих исходных данных: ü количество прибывших груженых контейнеров Nгрпр=120 конт/сут; ü количество отправленных груженых контейнеров Nгрот=110 конт/сут. Факторы, влияющие на величину суммарного материального потока. приведены в табл.1.1 Таблица 1.1
Методика и решение. Материальный поток — это совокупность товарно-материальных ценностей, рассматриваемая в процессе приложения к ним различных логистических операций и отнесенная к определенному временному интервалу. Входящий материальный поток — это поток, поступающий в логистическую систему из внешней среды. Для логистической системы «контейнерная площадка» входящий поток состоит из груженых и порожних контейнеров, выгружаемых на площадке из вагонов и автомобилей. Величина входящего потока определяется по формуле:
где Nпор — число порожних контейнеров, равное:
α* — доля порожних контейнеров, перегружаемых по прямому варианту, равная: α1 — если порожние контейнеры прибывают (Nгрпр<Nгрот), α2 — если порожние контейнеры отправляются (Nгрпр>Nгрот). Подставив исходные данные в формулу (1.1), получим:
Выходящий материальный поток — это поток, поступающий из логистической системы во внешнюю среду. Для логистической системы «контейнерная площадка» выходящий поток состоит из груженых и порожних контейнеров, перегружаемых с площадки в вагоны и автомобили. Величина выходящего потока в данном случае равна величине входящего потока:
Внутренний материальный поток — это поток, образуемый в результате осуществления логистических операций внутри логистической системы. Для логистической системы «контейнерная площадка» внутренний поток состоит из контейнеров, перемещаемых внутри площадки: в зону ремонта, в таможенную зону, при «свертывании» и «развертывании» площадки и т.д. Размер внутреннего потока определяется по формуле:
Его размер для заданных условий равен:
Внешний материальный поток — это поток, проходящий во внешней, по отношению к данной логистической системе, среде. Для логистической системы «контейнерная площадка» внешний поток состоит из контейнеров, перегружаемых по прямому варианту. Его величина определяется по формуле:
Для заданных условий его величина составит:
Суммарный материальный поток логистической системы определяется сложением материальных потоков, проходящих через ее отдельные участки и между участками. Величина суммарного материального потока определяется по формуле:
После подстановки вычисленных значений потоков получим:
Вывод. Суммарный суточный материальный поток в системе «контейнерная площадка» для заданных условий составляет 750 контейнеров. Варианты исходных данных (прил.1) для выполнения расчетов задается преподавателем. Прогнозирование материальных потоков Задача. Рассчитать прогнозируемое значение материального потока на 6 год при следующих исходных данных: за условный пятилетний период приведены в табл.2.1 Таблица 2.1 Изменение материального потока по годам
Методика и решение. Прогноз показателей функционирования логистической системы подразумевает оценку ожидаемых уровней спроса на продукцию, перевозки и т.д. в течение некоторого отрезка времени в будущем. В каждом конкретном случае оптимальный вариант прогнозирования выбирается на основании анализа состояния рынков сбыта, каналов распределения, методов планирования перевозок и т.д. Для прогнозирования материальных потоков могут быть использованы следующие методы прогнозирования. Метод наивного прогноза В этом случае прогнозируемый материальный поток принимается равным материальному потоку на конец анализируемого периода. Если обозначить прогноз как N(t+1), то получим:
В нашем случае значение прогноза на N(t+1) год составит: N(5+1)=N(5)=58,1 тыс. т/год Метод простой средней Значение прогноза рассчитывается как среднее арифметическое материальных потоков за предшествующие периоды:
где n — число значений материальных потоков, принятых для расчета;
Для исходных данных, приведенных в таблице 2.1, получим:
Метод скользящей средней Этот метод позволяет дать каждому значению материального потока оценку его веса. Метод предполагает, что значение анализируемой величины в конце предшествующего периода имеют большее влияние на прогнозируемое значение и должны иметь больший вес, а сумма весов за прогнозируемый период должна быть равна единице. При таких условиях значение прогноза рассчитывается по методу скользящей средней по формуле:
где αi — оценка веса i-го значения материального потока. Ограничение для αi имеет вид:
Для определения оценок веса αi можно использовать метод экспертных оценок. Предположим, что эксперты присвоили следующие оценки весов: α(1)=0,1, α(2)=0,1, α(3)=0,15, α(4)=0,25, α(5)=0,4. Расчет значения прогноза выполнен по формуле (2.3) при ограничении (2.4): N(5+1)=0,4·58,1+0,25·50,6+0,15·45,2+0,1·41,4+0,1·36,3=50,4 тыс. т/год
Метод регрессионного анализа Метод заключается в нахождении такой математической функции, которая обеспечивала бы описание изменения значений материального потока за предшествующие периоды и вычисление по этой функции значение прогноза. В общем виде уравнение искомой функции может быть записано следующим образом:
где F(t) — значение функции в t-й год; δ — погрешность, показывающая величину отклонения теоретических значений от экспериментальных.
Функция может иметь любой вид: полином, экспонента, логарифм и т.д. Выбор функции, наиболее точно описывающей заданные изменения материального потока осуществляется на основании минимизации значения погрешности δ, которое рассчитывается по формуле:
где N(t) — значение материального потока в t-й год (фактическое); n — число наблюдений; р — число параметров в уравнении тренда (число неизвестных).
Примем для анализа две функции: линейную и полином 2-го порядка:
где а — начальный уровень тренда; b — средний абсолютный прирост в единицу времени, константа линейного тренда; с — квадратичный параметр равный половине ускорения, константа параболического тренда. Значения коэффициентов a, b, c определены с помощью метода наименьших квадратов.
Продифференцируем каждое уравнение и составим систему нормальных уравнений: ü для линейного тренда:
ü для параболического тренда:
Для упрощения расчетов используем метод отсчета времени от условного начала. Обозначим в ряду изменения значений времени (t) таким образом, чтобы Представим метод расчета и его результаты в виде таблицы (табл.2.2). Таблица 2.2 Расчет параметров тренда
Перепишем уравнения с учетом ü для линейного тренда:
ü для параболического тренда:
Отсюда: ü для линейного тренда:
ü для параболического тренда:
Значения а и с найдем, решив систему методом определителей:
Рассчитанные значения f(ti) и f1(ti) при ti=[-2;2], и суммы квадратов разностей теоретических и практических значений приведены в табл.2.2 При t = –2 f(t-2)=46,32+5,28·(-2)=35,76 f1(t-2)=45,4+5,28·(-2)-0,46·4=33 При t = –1 f(t-1)=46,32+5,28·(-1)=35,76 f1(t-1)=45,4+5,28·(-1)-0,46·1=39,66=33 Для линейного тренда
Для параболического тренда
Так как 1,44<5,47, линейный тренд является боле предпочтительной функцией, т.е. F(t)=f(t). В этом случае прогноз искомого параметра целесообразно определять по формуле линейного тренда, т.е. F(3)=46,32+5,28·3=62,16 тыс. т/год Графики N(t) и F(t) приведены на рисунке 2.1.

Рис.2.1. Варианты исходных данных для выполнения индивидуальных заданий приведены в прил.2 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 — материальный поток за период ti.
— материальный поток за период ti. тыс. т/год
тыс. т/год

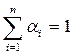


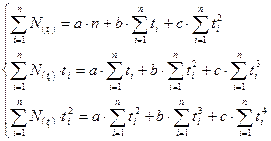
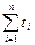 стала равна нулю.
стала равна нулю.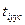



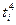



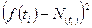


 и
и  :
: