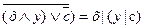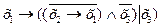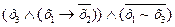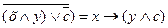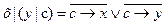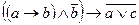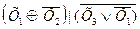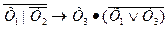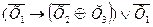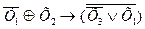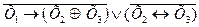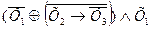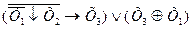|
|
Операция ИЛИ-НЕ стрелка Пирса (отрицание дизъюнкции)Нахождение истинности сложного высказывания ЦЕЛЬ РАБОТЫ 3.1.1 Изучить способы решения логических выражений. 3.1.2 Получить практические навыки по нахождению истинности сложного высказывания. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ 3.2.1 Методические указания по выполнению практической работы. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 3.3.1 Изучить основные способы решения логических выражений. 3.3.2 В соответствии с полученным вариантом выполнить задание. СОДЕРЖАНИЕ ОТЧЕТА 3.4.1 Цель работы. 3.4.2 Методические рекомендации. 3.4.3 Порядок выполнения работы. 3.4.4 Ответы на контрольные вопросы. 3.4.5 Выводы. КОНТРОЛЬНЫЕ ВОПРОСЫ 3.5.1 Логические операции. 3.5.2 Равносильность формул 3.5.3 Законы алгебры логики 3.5.4 Таблица истинности
ПРИЛОЖЕНИЕ 1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Операция отрицания НЕ (инверсия) Отрицанием высказывания А называется операция, результат которой F истинен, когда А ложно и ложен, когда А истинно. Отрицание обозначается черточкой над высказыванием А и читается так: F есть инверсия от А
Логическое сложение ИЛИ (дизъюнкция) Дизъюнкция – это логическая операция над двумя переменными А и В, результат F которой истинен, если хотя бы одна из составляющих его переменных истинна. Операция ИЛИ обозначается символом «V» или знаком «+»:
Логическое умножение И (конъюнкция) Конъюнкция – это логическая операция над двумя переменными А и В, результат F которой истинен, если истинны значения обеих переменных. Операция И обозначается символом «^» или знаком умножения «*»:
Операция равнозначности (эквивалентности) Эквивалентность – это логическая операция над двумя переменными А и В, результат F которой истинен, тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны. Операция Равнозначности обозначается символом «~» или «↔»:
Операция импликация Импликация – это логическая операция над двумя переменными А и В, результат F которой ложно, тогда и только тогда, когда одно высказывание истинно, а другое ложно. Операция Неравнозначности обозначается символом «→»:
Операция неравнозначности (сложение по модулю 2) Операция неравнозначности – функция истинна при неравных значениях переменных А и В. Операция сложение по модулю 2 обозначается символом «
Операция И-НЕ штрих Шеффера (отрицание конъюнкции) Штрих Шеффера – это функция, которая ложна только тогда, когда А и В истинны. В качестве знака этой операции используется символ «│»
F=A│B=
Операция ИЛИ-НЕ стрелка Пирса (отрицание дизъюнкции) Стрелка Пирса – функция, которая истинна только тогда, когда значения ее переменных А и В ложны. В качестве знака этой операции используется символ «↓»:
F=A↓B=
В математической логике, так же как и в алгебре, операции подчиняются определенным законам. С помощью этих законов (тождеств, равносильностей) можно упрощать составленные высказывания. Формулы, реализующие одну и ту же функцию, называются равносильными. 2 формулы называются равносильными,если при любых значениях х (всех переменных), входящих в эти формулы, эти формулы принимают одинаковое значение. Рассмотрим их для операций дизъюнкции и конъюнкции, учитывая свойство двойственности. Двойственность операций (таблица 1) заключается в том, что если в формуле, содержащей лишь операции дизъюнкции, конъюнкции и отрицания, заменить операции Законы Де Моргана называют переносом отрицания через логические связки. Таблица 1 -Законы алгебры логики
Приведем формулы с другими операциями, которые также будем считать основными:
Все эти формулы получаются простой проверкой по таблице истинности с четом истинности каждой операции, правильного раскрытия скобок и выполнения операций по приоритету. Знание законов математической логики помогает не только упрощать высказывания, но и правильно, логически рассуждать. Так, некоторые формулы помогают понять законы правильного мышления. С помощью введенных логических операций над высказываниями можно строить различные сложные высказывания. Использование скобок дает возможность установить порядок выполнения операций. Рассмотрим несколько примеров на установление истинности сложного высказывания. 1. Истинность сложного высказывания можно установить с помощью таблицы истинности (таблица 2). Введем порядок действий, определяющий последовательность столбцов в таблице истинности для высказывания 1) Таблица 2 -Таблица истинности для двух переменных
Для упрощения формул, содержащих скобки и различные логические операции, будем учитывать ряд правил. Так, при опускании скобок: o самой первой выполняется конъюнкция между элементарными высказываниями и их отрицаниями; o дизъюнкция выполняется раньше импликации и эквивалентности; o знак отрицания над формулой дает возможность опустить скобки, в которых эта формула заключена.
ПРИЛОЖЕНИЕ 2 КОНТРОЛЬНОЕ ЗАДАНИЕ Вариант 1 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 2 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 3 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 4 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности: (a | b) | c = a | (b | c) Вариант 5 1. Найдите истинность сложного высказывания: х1 ~ 2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 6 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 7 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 8 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 9 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 10 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 11 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности: (x | y) | c = x | (y | c) Вариант 12 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 13 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 14 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 15 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 16 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 17 1. Найдите истинность сложного высказывания: 2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 18 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 19 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности: (a | b) | c = a | (b | c) Вариант 20 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 21 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 22 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 23 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 24 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 25 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности: (a | b) | c = a | (b | c) Вариант 26 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 27 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 28 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 29 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 30 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 31 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности: (a | b) | c = a | (b | c) Вариант 32 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 33 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:
Вариант 34 1. Найдите истинность сложного высказывания:
2. Найдите корень логического уравнения, построением таблицы истинности:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

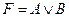 или
или 
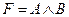 или
или 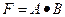 или F=А & В
или F=А & В или
или 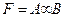
 или
или 
 »:
»:


 и
и 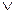 на
на 

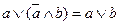

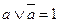

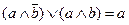

 - снятие двойного отрицания;
- снятие двойного отрицания; - снятие импликации;
- снятие импликации; - снятие эквивалентности;
- снятие эквивалентности; - снятие строгой дизъюнкции.
- снятие строгой дизъюнкции.
 ; 2)
; 2) 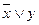 ; 3)
; 3) 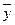 ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6) 
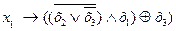

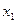 ~
~