Линейные дефекты (дислокации)

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Физический факультет

Кафедра физики полупроводников и микроэлектроники

Лабораторная работа

МЕТАЛЛОГРАФИЧЕСКОЕ ИЗУЧЕНИЕ ПОЛУПРОВОДНИКОВ

Воронеж 2005

Основные типы дефектов

Любое отклонение то периодической структуры кристалла называют дефектом.

Дефекты классифицируют по числу измерений, в которых нарушения кристалла простираются на расстояния, превышающие характерный параметр решетки. Выделяют точечные, линейные, поверхностные и объемные дефекты.

Точечные ( нульмерные ) дефекты

Размеры точечных дефектов во всех трех измерениях не превышают одного или нескольких межатомных расстояний. К ним относят вакансии, атомы в междоузлиях, атомы примесей в узлах или междоузлиях, а также сочетания примесь – вакансия, примесь – примесь, двойные и тройные вакансии и др.

Различают дефекты по Френкелю (рис.1а) и дефекты по Шоттки (рис.1б). Дефекты по Френкелю являются парными (вакансия – атом в междоузлии) и легче возникают в кристаллах, имеющих относительно рыхлые структуры (полупроводники со структурой алмаза - Ge,Si; вюрцита - CdS, CdSe, CdTe; сфалерита - GaAs,GaP,InSb). Дефекты по Шоттки преобладают в кристаллах с плотной упаковкой атомов (Mg, Be, Zn, Cd, Cu), где образование междоузельных атомов энергетически не выгодно. Они образуются, когда атомы из приповерхностного слоя выходят из кристалла на поверхность, а образовавшаяся вакансия мигрирует объем кристалла.

Рис.1. Точечные дефекты: а) Френкеля; б) Шоттки.

Вакансии являются равновесными дефектами, т.е. они всегда присутствуют в кристалле и их концентрация определяется термодинамическими условиями.

Равновесная концентрация пар Френкеля равна

, (1.1)

где N, N΄ - число атомов и междоузлий в единице объема, Е_ф – энергия образования пары.

Равновесная концентрация дефектов по Шоттки равна

, (1.2)

где E_v – энергия образования вакансий.

В общем случае кристалл содержит и дефекты по Френкелю и дефекты по Шоттки. Однако преобладают те нарушения, для образования которых требуется меньшая энергия.

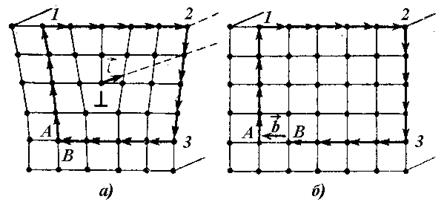
Линейные дефекты (дислокации)

Различают два основных типа дислокаций – краевую и винтовую. Промежуточные случаи можно считать комбинацией двух основных типов.

На рис.2 приведен пример краевой (линейной) дислокации. Дислокация образуется в результате сдвига верхней части кристалла относительно нижней части вдоль плоскости скольжения xz. В результате сдвига на один период решетки атомная плоскость верхней части кристалла не находит себе продолжения в нижней. Линия ЕЕ, являющаяся краем этой прерванной атомной плоскости внутри кристалла, называется краевой дислокацией.

Винтовые дислокации (дислокации Бюргерса) образуются, когда скольжение происходит параллельно линии дислокации (рис.3). Линией дислокации, или осью винтовой дислокации, является линия ЕЕ (рис.3в).

Рис.2. Линейная дислокация: а) образование; б) структура.

Рис.3. Винтовая дислокация: а) образование; б) структура вдоль оси дислокации; в) структура в плоскости сдвига: “○” , “+” – атомы нижележащей и вышележащей плоскостей, соответственно; “− − −” – атомный ряд, изогнутый при образовании дислокации

Рис.4 Контур Бюргерса в кристалле с краевой дислокацией (а) и в исходном идеальном кристалле (б).

Рис.5 Контур Бюргерса в кристалле с винтовой дислокацией (а) и в исходном идеальном кристалле (б).

Одной из важнейших характеристик дислокации является вектор смещения – вектор Бюргерса , определяемый следующим образом. Рассмотрим две кристаллические решетки: одну реальную, содержащую дефекты различного типа, и другую – идеальную, не содержащую никаких дефектов. Любую область реального кристалла, где можно установить взаимно однозначное соответствие с идеальным кристаллом, называют областью хорошего кристалла. Участки, где такое соответствие установить нельзя, называют областью плохого кристалла.

Контуром Бюргерса называют замкнутый контур произвольной формы, построенный в реальном кристалле так, что от атома к атому переходят последовательно, не выходя из области хорошего кристалла. Если в реальном кристалле контур проведен вокруг дислокации (рис.4а, рис.5а), то соответствующий контур в идеальном кристалле оказывается разомкнутым (рис.4б, рис.5б). Вектор, замыкающий контур в идеальном кристалле, называют вектором Бюргерса. Вектор Бюргерса всегда является одним из векторов трансляций решетки. Поэтому его модуль и направление ограничены рядом дискретных значений, определяемых структурой кристалла.

Между дислокациями существует сильное упругое взаимодействие. Дислокации, находящиеся на расстоянии ~ (10³÷10⁴)b, могут начать скольжение, вызванное полем упругих напряжений, которое создается вокруг дислокаций.

Энергия дислокации зависит от вектора Бюргерса по квадратичному закону:

, (1.3)

где G – модуль сдвига, R – внешний радиус дислокационной трубки (~10⁴b), r_o – радиус ядра дислокации (~b), ν – коэффициент Пуассона.

Количество дислокаций не зависит от температуры так как энергия образования дислокаций очень велика. Плотность дислокаций в кристаллt зависит в основном от его предшествующей истории, т.е. метода выращивания, способа и степени легирования, термической и механической обработок.

Не нашли, что искали? Воспользуйтесь поиском по сайту: