
|
|
Методы Эйлера и Рунге-Кутта.Принцип этих методов состоит в переходе от непрерывной искомой функции к дискретной, то есть существующей только для заданных значений аргумента. Значений аргумента не может быть много, так как при вычислениях накапливается ошибка. Шаг (
Количество шагов ( Метод Эйлераявляется самым простым. Он дает относительно большую погрешность, поэтому практически не применяется. Но позволяет понять принцип методов Рунге-Кутта. Пусть дано дифференциальное уравнение первого порядка Для первого значения аргумента:
Аналогично находят следующие значения функции:
По этим формулам находят все значения функции для заданных значений аргумента. Заметим, что расчетная формула является рекуррентной, то есть, чтобы найти значение
Метод Рунге-Куттапозволяет вычислитьзначения функции более точно. Его можно представить рекуррентными формулами нескольких порядков. Формулы более высокого порядка обеспечивают более высокую точность ( · Формула 1-го порядка
является формулой Эйлера. · Формула 2-го порядка
где
· Формула 3-го порядка
где
· Формула 4-го порядка
где
Формулы 2-го и 3-го порядка применяются для вычислений на калькуляторе, а формулы 4-го порядка – только на ЭВМ. Погрешности вычисленийобусловлены двумя причинами. Первая – переходом к дискретным значениям функции, что требует округления этих значений. Вторая – рекуррентностью расчетных формул, что приводит к накоплению погрешности. Уменьшение шага позволяет уменьшить погрешности. Однако при этом увеличивается число дискретов на заданном интервале аргумента. Что приводит к увеличению накопленной погрешности. Чтобы найти оптимальный шаг применяют оценки погрешностей расчетных формул. Они приведены рядом с расчетными формулами. Так, для формулы 4-го порядка оценка: ( Окончательно, чтобы после выполнения расчетов выяснить, достигнута ли требуемая точность, применяют прием Рунге. Он заключается в том, что расчеты повторяют с шагом, уменьшенным вдвое, и сравнивают результаты. Погрешность определяют по формуле
где
Если погрешность результатов вычислений оказалась больше заданной, то вычисления повторяют, уменьшив шаг ещё в 2 раза. После этого сравнивают результаты второго и третьего вычислений.
ПРИМЕР 4.1. Найти приближенное решение дифференциального уравнения РЕШЕНИЕ. Имеем дифференциальное уравнение первого порядка. Расчеты будем выполнять по формуле Рунге – Кутта 2-го порядка. Ширину шага аргумента берем из оценки: Число шагов: Вычисления выполняем в таблице 4.1. Вторые строки в "шапке" таблицы означают действия с числами соответствующих колонок. Стрелки означают, что числа надо брать из предыдущей строки. Например, вычисления второй строки:
Таблица 4.1.
Результаты решения представлены в колонках 1 и 6 таблицы. Вычисления выполнены с точностью выше требуемой на 2 знака. Согласно приему Рунге повторяем вычисления, уменьшив шаг вдвое ( Результаты вычислений приведены в таблице 4.2. Таблица 4.2.
Определяем погрешность согласно (4.8.):

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 интервал между смежными значениями аргумента) обычно берется постоянным.
интервал между смежными значениями аргумента) обычно берется постоянным.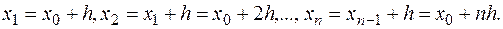
 ) определяется требуемой точностью.
) определяется требуемой точностью. и начальное условие
и начальное условие  .
. . Так как искомая функция дискретна, то производную нельзя понимать в полном смысле согласно её определению
. Так как искомая функция дискретна, то производную нельзя понимать в полном смысле согласно её определению
 , так как приращение аргумента не стремится к нулю, а является шагом вычислений (
, так как приращение аргумента не стремится к нулю, а является шагом вычислений ( 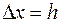 ). Поэтому можно записать приближение:
). Поэтому можно записать приближение: 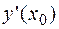
 . Тогда дифференциальное уравнение принимает вид:
. Тогда дифференциальное уравнение принимает вид: 

 . (4.1.)
. (4.1.)
 ,
,  (4.2.)
(4.2.)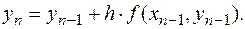
 надо знать предыдущее значение
надо знать предыдущее значение  . И, следовательно, ошибка, допущенная при вычислении
. И, следовательно, ошибка, допущенная при вычислении  ) при том же шаге (
) при том же шаге (  ). Метод позволяет дискретно решать дифференциальные уравнения 1-го порядка.
). Метод позволяет дискретно решать дифференциальные уравнения 1-го порядка.
 , (
, (  . (4.3.)
. (4.3.) (
(  (4.4.)
(4.4.)
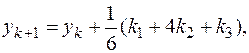 (
( 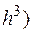 (4.5.)
(4.5.)
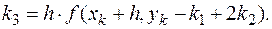
 (
( 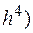 (4.6.)
(4.6.)

 . Например, при требуемой точности вычислений
. Например, при требуемой точности вычислений  , рекомендуется брать шаг аргумента
, рекомендуется брать шаг аргумента  .
. , (4.7.)
, (4.7.) приближенное решении е последнего вычисления при
приближенное решении е последнего вычисления при  ом шаге;
ом шаге; порядок используемой формулы. Так, если используется формула 2-го порядка, то
порядок используемой формулы. Так, если используется формула 2-го порядка, то  =2
=2 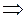

 . (4.8.)
. (4.8.) на отрезке
на отрезке  с точностью
с точностью  . Если
. Если 
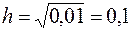 .
.
 = 0 – 1 = -1;
= 0 – 1 = -1;  = 0,1*(-1);
= 0,1*(-1);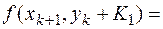 0,1- (1+(-0,1)) = -0,8;
0,1- (1+(-0,1)) = -0,8;  = 0,1*(-0,8) = -0,08;
= 0,1*(-0,8) = -0,08;  =1+
=1+  = 0,91.
= 0,91.
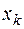







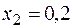



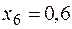




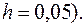 При этом в расчетной таблице в 3 и 5 колонках 5 умножение выполняют на 0,05, а не на 0,1, как в таблице 4.1.
При этом в расчетной таблице в 3 и 5 колонках 5 умножение выполняют на 0,05, а не на 0,1, как в таблице 4.1.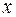

 Следовательно требуемая точность достигнута, и данные таблицы 4.2 являются искомым решением.
Следовательно требуемая точность достигнута, и данные таблицы 4.2 являются искомым решением.