
|
|
Расчётные сочетания усилий.Расчетные эпюры изгибающих моментов, эпюры продольных и поперечных сил приведены на рисунках Расчётным сечением является сечение 2 в элементе 3 с максимальным положительным изгибающим моментом и соответствующей продольной силе: Мрасч= +232,95 кН*м; Nсоотв= -229,46 кН. Расчётным сечением по отрицательному изгибающему моменту является сечении 3 загружение 5 элемент 28, с расчётным изгибающим моментом и соответствующей продольной силой: М= -225,32 кН*м; Nсоотв= -229.37 кН. Максимальное значение продольной силы в левой и правой опорах арки равно при загружении кратковременной снеговой нагрузкой по 2 – ому варианту загружения: Nоп= -435,99 кН; Qсоотв= 35,96 кН.
Расчёт элементов арки по предельным состояниям первой группы. Проверка прочности принятого сечения при положительном изгибающем моменте. Мрасч=+ 232,95 кН*м; Nсоотв= -229,46 кН; Fрасч= b×h = 0,205·0,957 = 0,196 м2 Wрасч = bh2/6 =0,205·0,9572 / 6 = 0,03129 м3 Проверяем прочность сечения по формуле 28 [1]:
где ξ – коэффициент, учитывающий дополнительный момент от продольной силы;
λx=L0/rx=12,13/0,277=43,86; rx=0,289×h=0,289·0,957=0,277м
Rс – расчетное сопротивление сжатию; Rс =Rcм= Rи =16*mв*mп*mсл*mб=16*1*0,8*1*0,8=10,24 МПа
Проверка прочности принятого сечения арки при отрицательном изгибающем моменте М= -225,32*м; Nсоотв= - 229,37 кН; Так как величина отрицательного изгибающего момента меньше положительного, а продольная сила изменилась незначительно, поэтому в данном случае необходимость проверку прочности сечения при отрицательном М отсутствует.
Рис. 5. Поперечное сечение арки
Проверка устойчивости арки в плоскости кривизны как центрально-сжатого стержня Расчётное усилие Nо = - 275,13 кН. Согласно п. 6.27 [1] проверку производим по формуле:
где φ - коэффициент продольного изгиба, определяемый по формуле 7 [2].
λx=L0/rx=13.44/0,277=48,54; rx=0,289×h=0,289·0,957=0,277 м L0=0,58*S=0.58*23.18=13.44 м Fрасч= b×h = 0,205·0,957 = 0,196 м2
Устойчивость арки в плоскости кривизны обеспечена.
Проверка устойчивости плоской формы деформирования арки При действии положительного изгибающего момента сжатой является верхняя кромка арки, к которой прикрепляются плиты покрытия. Расстояния между рабочими раскреплениями кромки составляет Lр=0,5 м. Растянутая кромка на такой длине не имеет закрепления, значит, проверка устойчивости производиться по формуле 33 [1]:
Расчётные усилия: N= -229,46 кН; Мд=254,59кН*м. n=2 - для элементов без закрепления растянутой зоны из плоскости деформирования, согласно п. 6.20 [2].
φм- коэффициент продольного изгиба, определяемый для гибкости участка элемента расчётной длинной Lp из плоскости деформирования, определяемый по формуле (23) [1]:
где kф=1 – коэффициент, зависящий от формы эпюры изгибающих моментов на участке Lp, определяемый по табл. 2 прил. 4 [1]; mб=0,8. Дальнейшие вычисления можно не выполнять, поскольку
При действии отрицательного изгибающего момента сжатой является нижняя кромка арки. Закрепление нижней кромки арки от выхода из плоскости изгиба осуществлена продольными связями. В левой полуарке в связи со значительной длиной дуги S1/2 = 11,59 м раскрепление нижней кромки производим в четырех точках с Lр=(11,59-1-1)/4=2,4м. Вертикальные продольные связи целесообразно расположить в каждой полуарке вблизи ключевого сечения и опорного башмака, на расстоянии 1,0м от их оси. Расчётное расстояние между точками раскрепления правой полуарки из плоскости изгиба составляет Lp=(11,59-1,0-1,0)/4=2,4м. Проверку устойчивости при действии отрицательного момента производим также по формуле 33 [1]:
n=1 - для элементов с закреплениями растянутой зоны из плоскости деформирования, согласно п. 6.20 [2]. М= -225,32кН*м; Nсоотв= - 229,37 кН; Nо = - 211,37кН.
λx=L0/rx=13,44/0,277=48,52; rx=0,289×h=0,289·0,957=0,277м L0=0,58×S=0,58×23,18=13,44 м Fрасч= b×h = 0,205·0,957 = 0,1962 м2 Wрасч=bh2/6=0,205·0,9572/6=31,29·10-3 м3
т.к. число закреплений растянутой кромки на участке lp=2.4 >4, то. коэф. m=1 по п.6.14 [2]
Дальнейшие вычисления можно не выполнять, поскольку
Расчёт и конструирование узлов арки. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
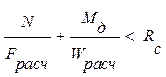
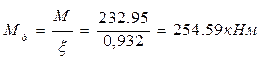 - изгибающий момент, определённый по деформированной схеме
- изгибающий момент, определённый по деформированной схеме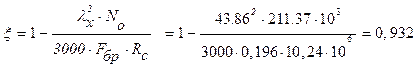
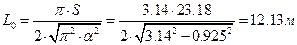
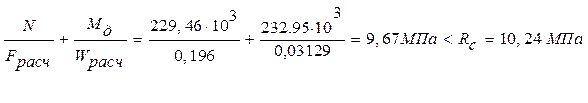
 Условие прочности выполнено.
Условие прочности выполнено.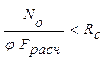
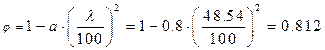
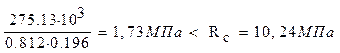
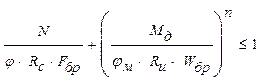
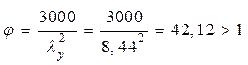
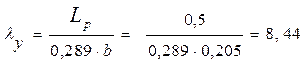
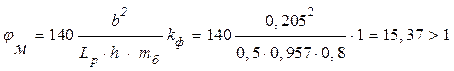
 и
и  , то проверка устойчивости плоской формы деформирования арки не требуется.
, то проверка устойчивости плоской формы деформирования арки не требуется.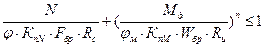
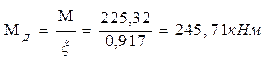
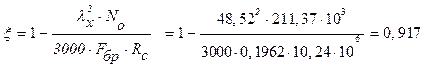

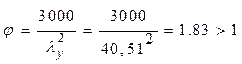
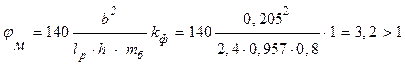
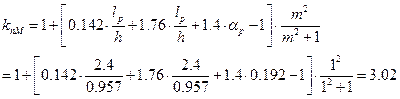
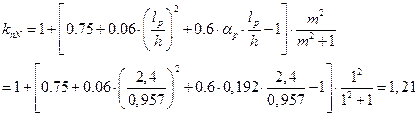
 =0.192 – центральный угол криволинейного участка lp=2.4,
=0.192 – центральный угол криволинейного участка lp=2.4, 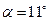
 то проверка устойчивости плоской формы деформирования арки не требуется.
то проверка устойчивости плоской формы деформирования арки не требуется.