|
Невыразимые предикаты: элиминация кванторов
Иногда всё не так просто. Просто – но не так J. Бывают сигнатуры, у которых просто нет ни одного автоморфизма. Но это отнюдь не означает, что в них выразимы все предикаты. Другой способ доказательства невыразимости – указать некоторое семейство Ξ предикатов, содержащее все выразимые предикаты, но не содержащее рассматриваемого. Очень часто семейство Ξ состоит из предикатов, выразимых бескванторными формулами. Для этого следует показать, что любая формула задаёт предикат, который можно задать и другой формулой, которая не содержит кванторов (формулы, задающие один и тот же предикат, назовём эквивалентными). Соответствующая процедура преобразования формул называется элиминацией (постепенным удалением) кванторов.
Пример 1.Плотный линейный порядок
Рассмотрим предметное множество Q с сигнатурой  и обычной интерпретацией. и обычной интерпретацией.
Теорема 7.2.Любая формула в этой интерпретации эквивалентна некоторой бескванторной формуле.
Доказательство.(а) Достаточно элиминировать один квантор: если их несколько, их можно элиминировать по одному изнутри. Можно считать, что этот квантор Е, потому что формулы  и и  эквивалентны. Итак, рассмотрим формулу вида эквивалентны. Итак, рассмотрим формулу вида  , выражающую некоторый n-местный предикат. При этом атомарные формулы имеют вид , выражающую некоторый n-местный предикат. При этом атомарные формулы имеют вид  или или  . Можно считать, что формула q записана в дизъюнктивной нормальной форме, то есть – в виде дизъюнкции конъюнкций формул вида . Можно считать, что формула q записана в дизъюнктивной нормальной форме, то есть – в виде дизъюнкции конъюнкций формул вида  , ,  , ,  и и  . Можно заменить . Можно заменить  на эквивалентную на эквивалентную  , а , а  – на эквивалентную – на эквивалентную  . После этого можно воспользоваться дистрибутивностью, получив ДНФ уже без отрицаний. . После этого можно воспользоваться дистрибутивностью, получив ДНФ уже без отрицаний.
(б) Заметим, что формулы  и и  эквивалентны (например, потому, что квантор существования есть своего рода «бесконечная дизъюнкция»!), поэтому достаточно научиться элиминировать квантор из формул вида эквивалентны (например, потому, что квантор существования есть своего рода «бесконечная дизъюнкция»!), поэтому достаточно научиться элиминировать квантор из формул вида  , где все , где все  – суть атомарные формулы следующих видов: – суть атомарные формулы следующих видов:  , ,  , ,  , , 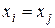 , ,  . Два последних типа атомарных формул не содержат переменную x, поэтому могут быть вынесены перед квантором, поэтому, не умаляя общности, можно считать, что все формулы . Два последних типа атомарных формул не содержат переменную x, поэтому могут быть вынесены перед квантором, поэтому, не умаляя общности, можно считать, что все формулы  содержат переменную x. содержат переменную x.
(в) Если среди атомарных формул есть формула вида  , то рассматриваемая формула эквивалентна бескванторной формуле , то рассматриваемая формула эквивалентна бескванторной формуле  , где формула , где формула  получается из формулы получается из формулы  заменой переменной x на переменную заменой переменной x на переменную  , так как во всех оценках, на которых истинна эта формула, переменные x и , так как во всех оценках, на которых истинна эта формула, переменные x и  должны принимать одинаковые значения. Поэтому можно считать, что все атомарные формулы должны принимать одинаковые значения. Поэтому можно считать, что все атомарные формулы  имеют вид имеют вид  или или  . .
(г) Переобозначим (для простоты) переменные, так, чтобы рассматриваемая формула приобрела вид  . Если все неравенства одного знака, то формула тождественно истинна (в Q нет наибольшего и наименьшего элементов). Если же присутствуют оба вида неравенств, то рассматриваемая формула означает, что существует некоторое число x, которое больше всех чисел . Если все неравенства одного знака, то формула тождественно истинна (в Q нет наибольшего и наименьшего элементов). Если же присутствуют оба вида неравенств, то рассматриваемая формула означает, что существует некоторое число x, которое больше всех чисел  и меньше всех чисел и меньше всех чисел  . Поскольку тех и других – конечное число, то (для рациональных чисел) это означает, что любое число . Поскольку тех и других – конечное число, то (для рациональных чисел) это означает, что любое число  меньше любого числа меньше любого числа  (потому что между любыми двумя рациональными числами найдётся ещё одно, например – их среднее арифметическое). Поэтому рассматриваемая формула эквивалентна (бескванторной!) конъюнкции всех формул вида (потому что между любыми двумя рациональными числами найдётся ещё одно, например – их среднее арифметическое). Поэтому рассматриваемая формула эквивалентна (бескванторной!) конъюнкции всех формул вида  . .
QED
Замечания.(1) Заменив Q на R, мы не почувствуем разницы. В действительности рассматривать R даже удобнее: в нужный момент можно просто сослаться на аксиому полноты. Вообще подойдёт любое плотное линейно упорядоченное множество без наибольшего и наименьшего элементов. Во всех этих интерпретациях истинны одни и те же формулы. Немного позднее мы назовём такие интерпретации элементарно эквивалентными.
(2) Бескванторная формула есть, по сути, формула пропозициональной логики (в которой простые высказывания – суть атомарные формулы). Поэтому теория плотного линейного порядка, состоящая из формул, истинных во всех рассмотренных интерпретациях, разрешима (как часть пропозициональной теории).
(3) Если добавить к рассматриваемой сигнатуре сложение и рациональные константы, то ситуация, как ни странно, не усложнится. Здесь поможет приём, который можно назвать «использование конечного представительного набора термов».
Теорема 7.3.Любая формула в сигнатуре  эквивалентна некоторой бескванторной формуле. Ситуация останется такой же, если рассмотреть любой другой набор рациональных констант, лишь бы в нём содержались как положительные, так и отрицательные числа. эквивалентна некоторой бескванторной формуле. Ситуация останется такой же, если рассмотреть любой другой набор рациональных констант, лишь бы в нём содержались как положительные, так и отрицательные числа.
Доказательство.Как уже (вскользь) отмечалось, квантор существования есть, по сути, «бесконечная дизъюнкция». Точнее, утверждение  равносильно «псевдоформуле» равносильно «псевдоформуле»  , где слева стоит дизъюнкция всех формул вида , где слева стоит дизъюнкция всех формул вида  при при  . Вполне возможно, что нет необходимости рассматривать «вот так прямо» все рациональные числа, а можно ограничиться некоторым их «представительным набором», отражающим все существенно различные случаи расположения значения переменной x относительно параметров формулы. Сигнатура, в которой нет сложения, не позволяет сконструировать таковой набор, но появления сложения и констант . Вполне возможно, что нет необходимости рассматривать «вот так прямо» все рациональные числа, а можно ограничиться некоторым их «представительным набором», отражающим все существенно различные случаи расположения значения переменной x относительно параметров формулы. Сигнатура, в которой нет сложения, не позволяет сконструировать таковой набор, но появления сложения и констант  такую возможность предоставляет. Правда при этом увеличивается и набор атомарных формул, но это обстоятельство оказывается непринципиальным. такую возможность предоставляет. Правда при этом увеличивается и набор атомарных формул, но это обстоятельство оказывается непринципиальным.
Действительно, атомарные формулы приобретут вид  или или  , где , где  – суть линейные комбинации переменных с целыми коэффициентами и, возможно, свободным членом, равным такой же линейной комбинации разрешённых констант. Откуда возьмутся целые коэффициенты (умножения-то нет)? Они возникнут из сумм вида – суть линейные комбинации переменных с целыми коэффициентами и, возможно, свободным членом, равным такой же линейной комбинации разрешённых констант. Откуда возьмутся целые коэффициенты (умножения-то нет)? Они возникнут из сумм вида  , которые естественно заменить на , которые естественно заменить на  . .
Любая такая атомарная формула эквивалентна «разрешённой» формуле вида  , ,  или или  : в формуле можно «по-школьному» выразить переменную x через остальные, получив линейную комбинацию, вообще говоря, с рациональными коэффициентами. Это не совсем хорошо, но в любой такой формуле можно (будет потом J) привести коэффициенты к общему знаменателю и на него умножить, получив нечто целочисленное. Отрицательные коэффициенты можно перенести на другую сторону, получив нечто выразимое в рассматриваемой сигнатуре. После этого следует рассмотреть «представительный набор термов», состоящий из всех получившихся термов : в формуле можно «по-школьному» выразить переменную x через остальные, получив линейную комбинацию, вообще говоря, с рациональными коэффициентами. Это не совсем хорошо, но в любой такой формуле можно (будет потом J) привести коэффициенты к общему знаменателю и на него умножить, получив нечто целочисленное. Отрицательные коэффициенты можно перенести на другую сторону, получив нечто выразимое в рассматриваемой сигнатуре. После этого следует рассмотреть «представительный набор термов», состоящий из всех получившихся термов  , их средних арифметических , их средних арифметических  , и сдвигов , и сдвигов  (или какие там у нас окажутся константы разных знаков…). Обозначим этот набор термов (или какие там у нас окажутся константы разных знаков…). Обозначим этот набор термов  . Теперь, очевидно, фрагмент формулы . Теперь, очевидно, фрагмент формулы  можно заменить на более длинный, зато – бескванторный и эквивалентный можно заменить на более длинный, зато – бескванторный и эквивалентный 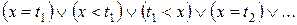
QED
Теорема 7.3. имеет любопытное следствие.
Теорема 7.4.Пусть единичный квадрат разрезан на несколько меньших квадратов. Тогда все они имеют рациональные стороны.
Доказательство.Пусть дано такое разрезание на n квадратов. Опишем его формулой, содержащей  параметров: n длин сторон квадратов, и параметров: n длин сторон квадратов, и 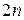 координат (например) левых нижних вершин квадратов (выписываются условия: квадраты содержатся внутри единичного квадрата, не пересекаются, покрывают все точки единичного квадрата). После этого на координаты вершин навешиваются кванторы существования, после чего образуется формула с n параметрами координат (например) левых нижних вершин квадратов (выписываются условия: квадраты содержатся внутри единичного квадрата, не пересекаются, покрывают все точки единичного квадрата). После этого на координаты вершин навешиваются кванторы существования, после чего образуется формула с n параметрами 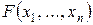 , которая истинна тогда и только тогда, когда единичный квадрат можно разрезать на квадраты со сторонами , которая истинна тогда и только тогда, когда единичный квадрат можно разрезать на квадраты со сторонами 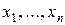 . .
Согласно теореме 7.3, эту формулу можно подвергнуть элиминации кванторов, после чего из неё получится бескванторная формула 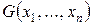 – логическая комбинация линейных уравнений и линейных неравенств (строгих: у нас есть только отношение <). На этом использование логических соображений заканчивается J. – логическая комбинация линейных уравнений и линейных неравенств (строгих: у нас есть только отношение <). На этом использование логических соображений заканчивается J.
Рассмотрим произвольное разрезание, пусть стороны квадратов этого разрезания – суть действительные числа  . Тогда . Тогда  . При этом некоторые равенства, которые входят в G становятся верными, а некоторые – нет. Рассмотрим те из них, которые оказались верными в этом случае, как систему линейных уравнений. Если эта система имеет ровно одно решение, то оно рационально (ну там – формула Крамера, метод исключения, любые подобные соображения…). Осталось показать, что это так и есть, то есть – эти уравнения «достаточно разнообразны». . При этом некоторые равенства, которые входят в G становятся верными, а некоторые – нет. Рассмотрим те из них, которые оказались верными в этом случае, как систему линейных уравнений. Если эта система имеет ровно одно решение, то оно рационально (ну там – формула Крамера, метод исключения, любые подобные соображения…). Осталось показать, что это так и есть, то есть – эти уравнения «достаточно разнообразны».
Пусть это не так. Тогда существует целая прямая, состоящая из решений этой системы. Пусть  – направляющий вектор этой прямой. Тогда существует достаточно малое число ε, такое, – направляющий вектор этой прямой. Тогда существует достаточно малое число ε, такое,  . Действительно, ε можно выбрать настолько малым, чтобы все неравенства, которые верны для набора . Действительно, ε можно выбрать настолько малым, чтобы все неравенства, которые верны для набора  остались бы верными и для набора остались бы верными и для набора  . Поэтому «с точки зрения» формулы G второй набор окажется неотличим от первого. . Поэтому «с точки зрения» формулы G второй набор окажется неотличим от первого.
Итак, получается, что единичный квадрат можно разрезать и на квадраты со сторонами  . Поэтому . Поэтому  на небольшом отрезке, но всё-таки – ненулевой длины. Левая часть этого равенства – квадратичный трёхчлен от ε. Он может быть тождественно равен константе только если его коэффициент при на небольшом отрезке, но всё-таки – ненулевой длины. Левая часть этого равенства – квадратичный трёхчлен от ε. Он может быть тождественно равен константе только если его коэффициент при  равен нулю, то есть равен нулю, то есть  , но это противоречит тому, что вектор , но это противоречит тому, что вектор  ненулевой. Полученное противоречие завершает доказательство. ненулевой. Полученное противоречие завершает доказательство.
QED
Замечание.Насколько существенна в этом доказательстве ссылка на возможность элиминации кванторов? Видя конкретное разрезание, систему линейных уравнений для сторон входящих в него квадратов написать нетрудно. Но всё-таки – почему такую систему можно написать всегда? Потому что трудно представить себе разрезание, для которого её нельзя написать, что ли J? Слабый аргумент…
Пример 2.Теория равенства
Случается, что все кванторы элиминировать невозможно. Например, рассмотрим сигнатуру  . Теорией равенства назовём множество всех формул этой сигнатуры, истинных во всех нормальных интерпретациях. Совершенно ясно, что формула . Теорией равенства назовём множество всех формул этой сигнатуры, истинных во всех нормальных интерпретациях. Совершенно ясно, что формула  выражает свойство «(в рассматриваемом множестве) существует не менее трёх различных элементов». Записать это свойство без кванторов невозможно (в рассматриваемой теории вообще мало что можно записать без кванторов). выражает свойство «(в рассматриваемом множестве) существует не менее трёх различных элементов». Записать это свойство без кванторов невозможно (в рассматриваемой теории вообще мало что можно записать без кванторов).
Значит ли это, что заниматься элиминацией кванторов в данном случае бессмысленно? Нет. Можно разделить все кванторы на «ручные», без которых невозможно обойтись, и которые ведут себя «контролируемо» и «не мешают», и «дикие», которые следует элиминировать. После этого (на самом деле – до J) за счёт расширения сигнатуры можно устранить и «ручные» кванторы.
Обозначим приведённую формулу символом  и определим аналогично счётное множество нульарных отношений и определим аналогично счётное множество нульарных отношений  , расширив тем самым рассматриваемую сигнатуру. Далее, будем рассматривать только те интерпретации, на которых символы , расширив тем самым рассматриваемую сигнатуру. Далее, будем рассматривать только те интерпретации, на которых символы  означают то же, что они означали до своего появления J. Произведённое расширение не меняет класса выразимых предикатов. Уменьшить его оно не может, не может и увеличить: все добавленные символы являются символами выразимых отношений. означают то же, что они означали до своего появления J. Произведённое расширение не меняет класса выразимых предикатов. Уменьшить его оно не может, не может и увеличить: все добавленные символы являются символами выразимых отношений.
Теорема 7.5.Рассматриваемая теория допускает элиминацию кванторов.
Доказательство.Как и в теореме 7.2, достаточно избавиться от одного квантора существования вида  , где р есть конъюнкция формул , где р есть конъюнкция формул  , ,  , ,  , ,  . Теперь элиминация кванторов сводится к нескольким простым замечаниям. . Теперь элиминация кванторов сводится к нескольким простым замечаниям.
а) Наличие формулы  позволяет сразу заменить рассматриваемую формулу эквивалентной бескванторной позволяет сразу заменить рассматриваемую формулу эквивалентной бескванторной  . .
б) Аналогично, формулы вида  можно удалить, просто уменьшив число переменных, если это не противоречит какой-то формуле вида можно удалить, просто уменьшив число переменных, если это не противоречит какой-то формуле вида  . Если же такое противоречие обнаружилось, формула является тождественно ложной. . Если же такое противоречие обнаружилось, формула является тождественно ложной.
в) Формулы вида  не содержат подкванторной переменной и могут быть вынесены перед квантором. Это приведёт к формуле вида не содержат подкванторной переменной и могут быть вынесены перед квантором. Это приведёт к формуле вида  . .
г) Заметим, что формула  эквивалентна формуле эквивалентна формуле  : утверждается наличие элемента, не совпадающего ни с одним из k отмеченных. : утверждается наличие элемента, не совпадающего ни с одним из k отмеченных.
QED
Пример 3.Теорема Тарского-Зайденберга
Теорема 7.6. (теорема Тарского-Зайденберга) В элементарной теории действительных чисел (сигнатура  ) выполнима элиминация кванторов. ) выполнима элиминация кванторов.
Замечания.
(1) Бескванторная формула рассматриваемой сигнатуры представляет собой совокупность (или одно, или другое…) нескольких систем алгебраических уравнений и неравенств. Множества, которые можно описать при помощи таких совокупностей, называются полуалгебраическими.
(2) Переход от формулы  к формуле к формуле  соответствует проектированию полуалгебраического множества параллельно оси x. Поэтому теорема Тарского-Зайденберга равносильна тому, что проекция полуалгебраического множества является полуалгебраическим множеством. соответствует проектированию полуалгебраического множества параллельно оси x. Поэтому теорема Тарского-Зайденберга равносильна тому, что проекция полуалгебраического множества является полуалгебраическим множеством.
(3) В частности, проекция полуалгебраического множества (на самом деле – просто алгебраического) в  , заданного уравнением , заданного уравнением  , вдоль оси x, есть полуалгебраическое множество. Немного подумав, мы даже можем написать неравенство, которое его описывает: , вдоль оси x, есть полуалгебраическое множество. Немного подумав, мы даже можем написать неравенство, которое его описывает:  . Соответствующая конструкция для алгебраических уравнений других видов тоже называется дискриминант. Теорема Тарского-Зайденберга гарантирует его существование в любой ситуации J. . Соответствующая конструкция для алгебраических уравнений других видов тоже называется дискриминант. Теорема Тарского-Зайденберга гарантирует его существование в любой ситуации J.
(4) Аналогично, рассмотрение системы двух алгебраических уравнений приводит к неконструктивному доказательству существования того, что обычно называют результантом.
(5) Практически все теоремы курса элементарной геометрии могут быть записаны в координатах. Возможность элиминации кванторов означает разрешимость соответствующей теории, так что из теоремы Тарского-Зайденберга следует разрешимость элементарной геометрии (которая была обещана в предисловии).
Доказательство.Как и ранее, достаточно элиминировать квантор из формулы  , где формула , где формула  уже является бескванторной. Следует доказать, что эта формула эквивалентна некоторой бескванторной формуле уже является бескванторной. Следует доказать, что эта формула эквивалентна некоторой бескванторной формуле  . Не умаляя общности, можно считать, что атомарные формулы, входящие в В, суть полиномиальные уравнения . Не умаляя общности, можно считать, что атомарные формулы, входящие в В, суть полиномиальные уравнения  или неравенства или неравенства  . .
Вспоминая, что  , мы обретаем возможность переписать эти формулы в виде уравнений и неравенств на многочлены от переменной x, коэффициенты которых являются многочленами от переменных , мы обретаем возможность переписать эти формулы в виде уравнений и неравенств на многочлены от переменной x, коэффициенты которых являются многочленами от переменных  . Формула . Формула  выражает некоторое свойство этих многочленов, и нам следует показать, что множество тех многочленов, для которых она истинна, является полуалгебраическим. выражает некоторое свойство этих многочленов, и нам следует показать, что множество тех многочленов, для которых она истинна, является полуалгебраическим.
С этой целью вводится понятие диаграммы набора многочленов. Пусть  , ,  , …, , …,  – набор многочленов. Пусть – набор многочленов. Пусть  – упорядоченный набор всех чисел, являющихся корнями каких-то многочленов рассмотренного набора. Составим таблицу, k строк которой соответствуют рассмотренным многочленам, а 2m+1 столбец – числам – упорядоченный набор всех чисел, являющихся корнями каких-то многочленов рассмотренного набора. Составим таблицу, k строк которой соответствуют рассмотренным многочленам, а 2m+1 столбец – числам  и интервалам между ними. Таблица заполнена символами +, – и 0, соответствующим тому, является ли многочлен положительным, отрицательным, или он равен нулю в соответствующей точке или на соответствующем промежутке. Эта таблица и называется диаграммой набора. и интервалам между ними. Таблица заполнена символами +, – и 0, соответствующим тому, является ли многочлен положительным, отрицательным, или он равен нулю в соответствующей точке или на соответствующем промежутке. Эта таблица и называется диаграммой набора.
Пример. Две тройки многочленов:  , ,  , 0 и , 0 и  , ,  , 0 имеют одинаковую диаграмму: , 0 имеют одинаковую диаграмму:

В том случае, когда коэффициенты многочленов от переменной x являются, в свою очередь, многочленами от переменных  , соответствующая диаграмма, конечно, тоже зависит от , соответствующая диаграмма, конечно, тоже зависит от  . При этом количество строк не меняется, а количество столбцов не превосходит числа . При этом количество строк не меняется, а количество столбцов не превосходит числа 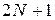 , где N – сумма степеней по переменной x рассматриваемых многочленов. Следовательно, количество возможных диаграмм для данного набора многочленов конечно, поэтому пространство , где N – сумма степеней по переменной x рассматриваемых многочленов. Следовательно, количество возможных диаграмм для данного набора многочленов конечно, поэтому пространство  всевозможных значений векторов всевозможных значений векторов  разбивается на конечное число частей, каждая из которых соответствует некоторой диаграмме. разбивается на конечное число частей, каждая из которых соответствует некоторой диаграмме.
Заметим, что для доказательства теоремы достаточно доказать, что все эти части будут полуалгебраическими множествами. Действительно, область истинности формулы  является объединением нескольких таких частей, тех самых, на которых все уравнения, входящие в формулу является объединением нескольких таких частей, тех самых, на которых все уравнения, входящие в формулу  обращаются в верные равенства, а все неравенства имеют верный знак для какой-то конъюнкции, входящей в ДНФ (не умаляя общности можно считать, что обращаются в верные равенства, а все неравенства имеют верный знак для какой-то конъюнкции, входящей в ДНФ (не умаляя общности можно считать, что  есть ДНФ). есть ДНФ).
Теперь приступим к изложению доказательства заявленного факта.
Во-первых, заметим, что уменьшение набора многочленов не может разрушить это свойство. В самом деле, диаграмма многочленов меньшего семейства получается из диаграммы для большего семейства удалением лишних строк и слиянием соседних столбцов, оказавшихся после удаления строк идентичными (такие наборы столбцов возникают на месте столбцов, соответствовавших корням удалённых многочленов и соседних с ними). При этом, возможно, некоторые «соседние» части сливаются в одну, но объединение частей не может лишить их свойства «быть полуалгебраическими множествами». Поэтому утверждение необязательно доказывать для множества всевозможных наборов многочленов. Можно ограничиться рассмотрением некоторого множества наборов многочленов, такого что для любого набора в этом множестве найдётся некоторый набор, содержащий данный (больший по включению). Другими словами, при необходимости мы всегда можем добавить к рассматриваемому набору любое конечное множество «новых» многочленов.
Во-вторых, рассмотрим следующие четыре операции над многочленами.
а) Отбрасывание старшего (по переменной x) члена некоторого многочлена из набора. Эта операция уменьшает на единицу степень «оперируемого» многочлена.
б) Взятие старшего (снова по переменной x) коэффициента некоторого многочлена. Степень многочлена при этом уменьшается до нуля.
в) Дифференцирование некоторого многочлена по переменной x.
г) Взятие модифицированного остатка от деления одного многочлена на другой.
Введение понятия модифицированного остатка связано с тем, что кольцо  , как и , как и  не является, вообще говоря, евклидовым. При делении «уголком» часто приходится делить на старший коэффициент делимого (поэтому в кольце не является, вообще говоря, евклидовым. При делении «уголком» часто приходится делить на старший коэффициент делимого (поэтому в кольце  обычное деление с остатком возможно лишь на многочлены со старшими коэффициентами обычное деление с остатком возможно лишь на многочлены со старшими коэффициентами  ). Для получения модифицированного остатка, который в ). Для получения модифицированного остатка, который в  определён всегда, требуется предварительно умножить делимое на некоторую степень старшего коэффициента делителя, необходимую для того, чтобы деление с остатком можно было бы произвести. Очевидно, что достаточно умножить делимый многочлен на определён всегда, требуется предварительно умножить делимое на некоторую степень старшего коэффициента делителя, необходимую для того, чтобы деление с остатком можно было бы произвести. Очевидно, что достаточно умножить делимый многочлен на  , где , где 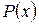 – делимое, – делимое,  – делитель, – делитель,  –старший коэффициент –старший коэффициент  . Окончательно: модифицированным остатком от деления многочлена . Окончательно: модифицированным остатком от деления многочлена 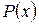 на многочлен на многочлен  в кольце в кольце  называется остаток от деления на называется остаток от деления на  многочлена многочлена  (при этом, разумеется, можно предполагать, что (при этом, разумеется, можно предполагать, что 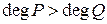 , иначе деление происходит тривиально и модифицированный остаток есть , иначе деление происходит тривиально и модифицированный остаток есть  ). ).
Совершенно очевидно, что для любого конечного набора многочленов из кольца  существует также конечный (но гораздо больший!) набор многочленов, содержащий исходный и замкнутый относительно рассмотренных операций. Поэтому, не умаляя общности, можно ограничиться рассмотрением только таких наборов многочленов. существует также конечный (но гораздо больший!) набор многочленов, содержащий исходный и замкнутый относительно рассмотренных операций. Поэтому, не умаляя общности, можно ограничиться рассмотрением только таких наборов многочленов.
В третьих, имеет место следующее утверждение.
Лемма 7.7. Пусть F – конечное множество многочленов кольца  , замкнутое относительно рассмотренных четырёх операций, , замкнутое относительно рассмотренных четырёх операций,  – подмножество этого множества, состоящее из многочленов нулевой степени (по переменной x). Тогда диаграмма множества F при данных значениях переменных – подмножество этого множества, состоящее из многочленов нулевой степени (по переменной x). Тогда диаграмма множества F при данных значениях переменных  однозначно определяется соответствующей диаграммой для множества однозначно определяется соответствующей диаграммой для множества  . .
Доказательство леммы 7.7. Достаточно показать, что добавление к множеству многочленов ещё одного, такого, что результаты всех операций с ним и уже имеющимися в множестве многочленами также лежат в этом множестве, соответствует некоторому однозначно определённому преобразованию диаграммы множества. При этом многочлены можно добавлять в порядке неубывания их степеней. Если начать эту процедуру с множества  , то, в силу конечности множества F мы через конечное число шагов доберёмся до множества F. При этом преобразование диаграммы на каждом шаге будет однозначным, поэтому «окончательная» диаграмма (для множества F) однозначно определяется «исходной» (для множества , то, в силу конечности множества F мы через конечное число шагов доберёмся до множества F. При этом преобразование диаграммы на каждом шаге будет однозначным, поэтому «окончательная» диаграмма (для множества F) однозначно определяется «исходной» (для множества  ). ).
Итак, пусть на очередном шаге мы добавили к множеству многочлен 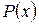 . Поскольку все необходимые многочлены меньших степеней в множестве уже содержатся, там уже содержится старший коэффициент многочлена . Поскольку все необходимые многочлены меньших степеней в множестве уже содержатся, там уже содержится старший коэффициент многочлена 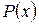 . Следовательно, в диаграмме уже содержится соответствующая строка. Если в ней содержатся только нули, то при данных значениях переменных . Следовательно, в диаграмме уже содержится соответствующая строка. Если в ней содержатся только нули, то при данных значениях переменных  многочлен многочлен 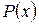 совпадает с многочленом, полученным из совпадает с многочленом, полученным из 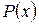 отбрасыванием старшего члена, который тоже уже содержится в множестве, и нам, попросту, следует продублировать соответствующую строку диаграммы. отбрасыванием старшего члена, который тоже уже содержится в множестве, и нам, попросту, следует продублировать соответствующую строку диаграммы.
Осталось рассмотреть случай, когда старший коэффициент не равен нулю. При этом пополнение диаграммы будет происходить в два этапа. На первом этапе мы заполним для нового многочлена все имеющиеся к текущему моменту столбцы диаграммы. На втором этапе мы увеличим количество столбцов диаграммы за счёт «новых» корней многочлена 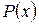 , не являющихся корнями никаких многочленов, ранее входивших в множество, и заполним соответствующие столбцы для всех многочленов. , не являющихся корнями никаких многочленов, ранее входивших в множество, и заполним соответствующие столбцы для всех многочленов.
Первый этап. Определим сначала знаки многочлена 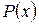 в столбцах, соответствующих корням «старых» многочленов. Пусть столбец соответствует корню α многочлена в столбцах, соответствующих корням «старых» многочленов. Пусть столбец соответствует корню α многочлена  . Можно считать, что его старший коэффициент отличен от нуля при данных значениях переменных . Можно считать, что его старший коэффициент отличен от нуля при данных значениях переменных  (иначе его можно отбросить, перейдя к другому уже имеющемуся многочлену). Знак этого старшего коэффициента многочлена (иначе его можно отбросить, перейдя к другому уже имеющемуся многочлену). Знак этого старшего коэффициента многочлена  тоже известен, так как в множестве содержится соответствующая этому коэффициенту строка. Применим к многочленам тоже известен, так как в множестве содержится соответствующая этому коэффициенту строка. Применим к многочленам 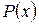 и и  операцию модифицированного деления с остатком: операцию модифицированного деления с остатком:  . Заметим, что . Заметим, что  , так как , так как  , многочлены , многочлены  и β содержатся в множестве, поэтому знак многочлена и β содержатся в множестве, поэтому знак многочлена 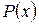 в точке α определяется однозначно. в точке α определяется однозначно.
Далее, определим, на каких участках, соответствующих столбцам диаграммы, содержатся «новые» корни многочлена 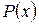 . Для этого вспомним, что в множестве содержится производная по переменной x этого многочлена. . Для этого вспомним, что в множестве содержится производная по переменной x этого многочлена.
а) Если в двух столбцах, соответствующих соседним «старым» корням многочлен 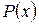 имеет один и тот же знак, то он имеет этот же знак и на промежутке между этими корнями. Действительно, будь это не так, между этими «старыми» корнями обязательно бы находился экстремум многочлена, то есть – корень его производной, и корни не были бы соседними корнями диаграммы. имеет один и тот же знак, то он имеет этот же знак и на промежутке между этими корнями. Действительно, будь это не так, между этими «старыми» корнями обязательно бы находился экстремум многочлена, то есть – корень его производной, и корни не были бы соседними корнями диаграммы.
б) Если в одном из соседних столбцов, или в обоих столбцах, соответствующих «старым» корням многочлен 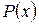 принимает значение 0, то в интервале между этими корнями многочлен принимает значение 0, то в интервале между этими корнями многочлен 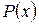 также не имеет корней, иначе эти корни снова не были бы соседними в силу теоремы Ролля: «между корнями функции есть корень производной». также не имеет корней, иначе эти корни снова не были бы соседними в силу теоремы Ролля: «между корнями функции есть корень производной».
в) Если в соседних столбцах многочлен 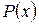 имеет разные знаки, то один корень на соответствующем интервале у многочлена имеется по крайней мере один корень (теорема Больцано-Коши). Но два или более их быть не может (снова по теореме Ролля), поэтому такой корень ровно один, и рассматриваемый столбец диаграммы превращается в три. При этом понятно, как заполняются клетки этих столбцов, соответствующие многочлену имеет разные знаки, то один корень на соответствующем интервале у многочлена имеется по крайней мере один корень (теорема Больцано-Коши). Но два или более их быть не может (снова по теореме Ролля), поэтому такой корень ровно один, и рассматриваемый столбец диаграммы превращается в три. При этом понятно, как заполняются клетки этих столбцов, соответствующие многочлену 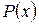 . .
г) Аналогично проводится рассуждение и для лучей, находящихся на краях диаграммы: там знак многочлена в пределе определяется знаком его старшего коэффициента.
Второй этап оказывается тривиален. «Новые» корни ничем не хуже «старых», и заполнить для них остальные строки диаграммы, начав с самого низа, не составляет труда (а знаки старших коэффициентов, находящихся на нижнем уровне, постоянны во всей диаграмме). Тем самым, доказательство леммы 7.7 завершено.
QED
Завершение доказательства теоремы 7.6.теперь тоже почти тривиально: как уже говорилось, диаграмма для множества  состоит из строк-«констант», поэтому на этом этапе диаграмма состоит всего из одного столбца. Поэтому различным вариантам этих диаграмм соответствуют различные варианты полуалгебраических множеств. Эти множества и составляют искомое разбиение. состоит из строк-«констант», поэтому на этом этапе диаграмма состоит всего из одного столбца. Поэтому различным вариантам этих диаграмм соответствуют различные варианты полуалгебраических множеств. Эти множества и составляют искомое разбиение.
QED
Учебное издание
Пушкарёв Игорь Александрович
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКУЮ ЛОГИКУ
Учебное пособие
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 и обычной интерпретацией.
и обычной интерпретацией. и
и  эквивалентны. Итак, рассмотрим формулу вида
эквивалентны. Итак, рассмотрим формулу вида  , выражающую некоторый n-местный предикат. При этом атомарные формулы имеют вид
, выражающую некоторый n-местный предикат. При этом атомарные формулы имеют вид  или
или  . Можно считать, что формула q записана в дизъюнктивной нормальной форме, то есть – в виде дизъюнкции конъюнкций формул вида
. Можно считать, что формула q записана в дизъюнктивной нормальной форме, то есть – в виде дизъюнкции конъюнкций формул вида  и
и  . Можно заменить
. Можно заменить  , а
, а  . После этого можно воспользоваться дистрибутивностью, получив ДНФ уже без отрицаний.
. После этого можно воспользоваться дистрибутивностью, получив ДНФ уже без отрицаний. и
и  эквивалентны (например, потому, что квантор существования есть своего рода «бесконечная дизъюнкция»!), поэтому достаточно научиться элиминировать квантор из формул вида
эквивалентны (например, потому, что квантор существования есть своего рода «бесконечная дизъюнкция»!), поэтому достаточно научиться элиминировать квантор из формул вида  , где все
, где все  – суть атомарные формулы следующих видов:
– суть атомарные формулы следующих видов:  ,
,  ,
,  ,
, 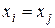 ,
,  . Два последних типа атомарных формул не содержат переменную x, поэтому могут быть вынесены перед квантором, поэтому, не умаляя общности, можно считать, что все формулы
. Два последних типа атомарных формул не содержат переменную x, поэтому могут быть вынесены перед квантором, поэтому, не умаляя общности, можно считать, что все формулы  , где формула
, где формула  получается из формулы
получается из формулы  , так как во всех оценках, на которых истинна эта формула, переменные x и
, так как во всех оценках, на которых истинна эта формула, переменные x и  . Если все неравенства одного знака, то формула тождественно истинна (в Q нет наибольшего и наименьшего элементов). Если же присутствуют оба вида неравенств, то рассматриваемая формула означает, что существует некоторое число x, которое больше всех чисел
. Если все неравенства одного знака, то формула тождественно истинна (в Q нет наибольшего и наименьшего элементов). Если же присутствуют оба вида неравенств, то рассматриваемая формула означает, что существует некоторое число x, которое больше всех чисел  . Поскольку тех и других – конечное число, то (для рациональных чисел) это означает, что любое число
. Поскольку тех и других – конечное число, то (для рациональных чисел) это означает, что любое число  .
. эквивалентна некоторой бескванторной формуле. Ситуация останется такой же, если рассмотреть любой другой набор рациональных констант, лишь бы в нём содержались как положительные, так и отрицательные числа.
эквивалентна некоторой бескванторной формуле. Ситуация останется такой же, если рассмотреть любой другой набор рациональных констант, лишь бы в нём содержались как положительные, так и отрицательные числа. равносильно «псевдоформуле»
равносильно «псевдоформуле»  , где слева стоит дизъюнкция всех формул вида
, где слева стоит дизъюнкция всех формул вида  при
при  . Вполне возможно, что нет необходимости рассматривать «вот так прямо» все рациональные числа, а можно ограничиться некоторым их «представительным набором», отражающим все существенно различные случаи расположения значения переменной x относительно параметров формулы. Сигнатура, в которой нет сложения, не позволяет сконструировать таковой набор, но появления сложения и констант
. Вполне возможно, что нет необходимости рассматривать «вот так прямо» все рациональные числа, а можно ограничиться некоторым их «представительным набором», отражающим все существенно различные случаи расположения значения переменной x относительно параметров формулы. Сигнатура, в которой нет сложения, не позволяет сконструировать таковой набор, но появления сложения и констант  такую возможность предоставляет. Правда при этом увеличивается и набор атомарных формул, но это обстоятельство оказывается непринципиальным.
такую возможность предоставляет. Правда при этом увеличивается и набор атомарных формул, но это обстоятельство оказывается непринципиальным. или
или  , где
, где  – суть линейные комбинации переменных с целыми коэффициентами и, возможно, свободным членом, равным такой же линейной комбинации разрешённых констант. Откуда возьмутся целые коэффициенты (умножения-то нет)? Они возникнут из сумм вида
– суть линейные комбинации переменных с целыми коэффициентами и, возможно, свободным членом, равным такой же линейной комбинации разрешённых констант. Откуда возьмутся целые коэффициенты (умножения-то нет)? Они возникнут из сумм вида  , которые естественно заменить на
, которые естественно заменить на  .
. ,
,  или
или  : в формуле можно «по-школьному» выразить переменную x через остальные, получив линейную комбинацию, вообще говоря, с рациональными коэффициентами. Это не совсем хорошо, но в любой такой формуле можно (будет потом J) привести коэффициенты к общему знаменателю и на него умножить, получив нечто целочисленное. Отрицательные коэффициенты можно перенести на другую сторону, получив нечто выразимое в рассматриваемой сигнатуре. После этого следует рассмотреть «представительный набор термов», состоящий из всех получившихся термов
: в формуле можно «по-школьному» выразить переменную x через остальные, получив линейную комбинацию, вообще говоря, с рациональными коэффициентами. Это не совсем хорошо, но в любой такой формуле можно (будет потом J) привести коэффициенты к общему знаменателю и на него умножить, получив нечто целочисленное. Отрицательные коэффициенты можно перенести на другую сторону, получив нечто выразимое в рассматриваемой сигнатуре. После этого следует рассмотреть «представительный набор термов», состоящий из всех получившихся термов  , их средних арифметических
, их средних арифметических  , и сдвигов
, и сдвигов  (или какие там у нас окажутся константы разных знаков…). Обозначим этот набор термов
(или какие там у нас окажутся константы разных знаков…). Обозначим этот набор термов  . Теперь, очевидно, фрагмент формулы
. Теперь, очевидно, фрагмент формулы  можно заменить на более длинный, зато – бескванторный и эквивалентный
можно заменить на более длинный, зато – бескванторный и эквивалентный 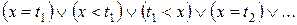
 параметров: n длин сторон квадратов, и
параметров: n длин сторон квадратов, и 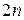 координат (например) левых нижних вершин квадратов (выписываются условия: квадраты содержатся внутри единичного квадрата, не пересекаются, покрывают все точки единичного квадрата). После этого на координаты вершин навешиваются кванторы существования, после чего образуется формула с n параметрами
координат (например) левых нижних вершин квадратов (выписываются условия: квадраты содержатся внутри единичного квадрата, не пересекаются, покрывают все точки единичного квадрата). После этого на координаты вершин навешиваются кванторы существования, после чего образуется формула с n параметрами 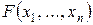 , которая истинна тогда и только тогда, когда единичный квадрат можно разрезать на квадраты со сторонами
, которая истинна тогда и только тогда, когда единичный квадрат можно разрезать на квадраты со сторонами 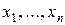 .
.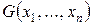 – логическая комбинация линейных уравнений и линейных неравенств (строгих: у нас есть только отношение <). На этом использование логических соображений заканчивается J.
– логическая комбинация линейных уравнений и линейных неравенств (строгих: у нас есть только отношение <). На этом использование логических соображений заканчивается J. . Тогда
. Тогда  . При этом некоторые равенства, которые входят в G становятся верными, а некоторые – нет. Рассмотрим те из них, которые оказались верными в этом случае, как систему линейных уравнений. Если эта система имеет ровно одно решение, то оно рационально (ну там – формула Крамера, метод исключения, любые подобные соображения…). Осталось показать, что это так и есть, то есть – эти уравнения «достаточно разнообразны».
. При этом некоторые равенства, которые входят в G становятся верными, а некоторые – нет. Рассмотрим те из них, которые оказались верными в этом случае, как систему линейных уравнений. Если эта система имеет ровно одно решение, то оно рационально (ну там – формула Крамера, метод исключения, любые подобные соображения…). Осталось показать, что это так и есть, то есть – эти уравнения «достаточно разнообразны». – направляющий вектор этой прямой. Тогда существует достаточно малое число ε, такое,
– направляющий вектор этой прямой. Тогда существует достаточно малое число ε, такое,  . Действительно, ε можно выбрать настолько малым, чтобы все неравенства, которые верны для набора
. Действительно, ε можно выбрать настолько малым, чтобы все неравенства, которые верны для набора  . Поэтому «с точки зрения» формулы G второй набор окажется неотличим от первого.
. Поэтому «с точки зрения» формулы G второй набор окажется неотличим от первого. на небольшом отрезке, но всё-таки – ненулевой длины. Левая часть этого равенства – квадратичный трёхчлен от ε. Он может быть тождественно равен константе только если его коэффициент при
на небольшом отрезке, но всё-таки – ненулевой длины. Левая часть этого равенства – квадратичный трёхчлен от ε. Он может быть тождественно равен константе только если его коэффициент при  равен нулю, то есть
равен нулю, то есть  , но это противоречит тому, что вектор
, но это противоречит тому, что вектор  . Теорией равенства назовём множество всех формул этой сигнатуры, истинных во всех нормальных интерпретациях. Совершенно ясно, что формула
. Теорией равенства назовём множество всех формул этой сигнатуры, истинных во всех нормальных интерпретациях. Совершенно ясно, что формула  выражает свойство «(в рассматриваемом множестве) существует не менее трёх различных элементов». Записать это свойство без кванторов невозможно (в рассматриваемой теории вообще мало что можно записать без кванторов).
выражает свойство «(в рассматриваемом множестве) существует не менее трёх различных элементов». Записать это свойство без кванторов невозможно (в рассматриваемой теории вообще мало что можно записать без кванторов). и определим аналогично счётное множество нульарных отношений
и определим аналогично счётное множество нульарных отношений  , расширив тем самым рассматриваемую сигнатуру. Далее, будем рассматривать только те интерпретации, на которых символы
, расширив тем самым рассматриваемую сигнатуру. Далее, будем рассматривать только те интерпретации, на которых символы  , где р есть конъюнкция формул
, где р есть конъюнкция формул  ,
,  ,
,  ,
,  . Теперь элиминация кванторов сводится к нескольким простым замечаниям.
. Теперь элиминация кванторов сводится к нескольким простым замечаниям. .
. .
. эквивалентна формуле
эквивалентна формуле  : утверждается наличие элемента, не совпадающего ни с одним из k отмеченных.
: утверждается наличие элемента, не совпадающего ни с одним из k отмеченных. ) выполнима элиминация кванторов.
) выполнима элиминация кванторов. к формуле
к формуле  соответствует проектированию полуалгебраического множества параллельно оси x. Поэтому теорема Тарского-Зайденберга равносильна тому, что проекция полуалгебраического множества является полуалгебраическим множеством.
соответствует проектированию полуалгебраического множества параллельно оси x. Поэтому теорема Тарского-Зайденберга равносильна тому, что проекция полуалгебраического множества является полуалгебраическим множеством. , заданного уравнением
, заданного уравнением  , вдоль оси x, есть полуалгебраическое множество. Немного подумав, мы даже можем написать неравенство, которое его описывает:
, вдоль оси x, есть полуалгебраическое множество. Немного подумав, мы даже можем написать неравенство, которое его описывает:  . Соответствующая конструкция для алгебраических уравнений других видов тоже называется дискриминант. Теорема Тарского-Зайденберга гарантирует его существование в любой ситуации J.
. Соответствующая конструкция для алгебраических уравнений других видов тоже называется дискриминант. Теорема Тарского-Зайденберга гарантирует его существование в любой ситуации J. , где формула
, где формула  уже является бескванторной. Следует доказать, что эта формула эквивалентна некоторой бескванторной формуле
уже является бескванторной. Следует доказать, что эта формула эквивалентна некоторой бескванторной формуле  . Не умаляя общности, можно считать, что атомарные формулы, входящие в В, суть полиномиальные уравнения
. Не умаляя общности, можно считать, что атомарные формулы, входящие в В, суть полиномиальные уравнения  или неравенства
или неравенства  .
. , мы обретаем возможность переписать эти формулы в виде уравнений и неравенств на многочлены от переменной x, коэффициенты которых являются многочленами от переменных
, мы обретаем возможность переписать эти формулы в виде уравнений и неравенств на многочлены от переменной x, коэффициенты которых являются многочленами от переменных  ,
,  , …,
, …,  – набор многочленов. Пусть
– набор многочленов. Пусть  – упорядоченный набор всех чисел, являющихся корнями каких-то многочленов рассмотренного набора. Составим таблицу, k строк которой соответствуют рассмотренным многочленам, а 2m+1 столбец – числам
– упорядоченный набор всех чисел, являющихся корнями каких-то многочленов рассмотренного набора. Составим таблицу, k строк которой соответствуют рассмотренным многочленам, а 2m+1 столбец – числам  и интервалам между ними. Таблица заполнена символами +, – и 0, соответствующим тому, является ли многочлен положительным, отрицательным, или он равен нулю в соответствующей точке или на соответствующем промежутке. Эта таблица и называется диаграммой набора.
и интервалам между ними. Таблица заполнена символами +, – и 0, соответствующим тому, является ли многочлен положительным, отрицательным, или он равен нулю в соответствующей точке или на соответствующем промежутке. Эта таблица и называется диаграммой набора. ,
,  , 0 и
, 0 и  ,
,  , 0 имеют одинаковую диаграмму:
, 0 имеют одинаковую диаграмму:
 , соответствующая диаграмма, конечно, тоже зависит от
, соответствующая диаграмма, конечно, тоже зависит от  . При этом количество строк не меняется, а количество столбцов не превосходит числа
. При этом количество строк не меняется, а количество столбцов не превосходит числа 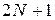 , где N – сумма степеней по переменной x рассматриваемых многочленов. Следовательно, количество возможных диаграмм для данного набора многочленов конечно, поэтому пространство
, где N – сумма степеней по переменной x рассматриваемых многочленов. Следовательно, количество возможных диаграмм для данного набора многочленов конечно, поэтому пространство  всевозможных значений векторов
всевозможных значений векторов  разбивается на конечное число частей, каждая из которых соответствует некоторой диаграмме.
разбивается на конечное число частей, каждая из которых соответствует некоторой диаграмме. , как и
, как и  не является, вообще говоря, евклидовым. При делении «уголком» часто приходится делить на старший коэффициент делимого (поэтому в кольце
не является, вообще говоря, евклидовым. При делении «уголком» часто приходится делить на старший коэффициент делимого (поэтому в кольце  , где
, где 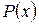 – делимое,
– делимое,  – делитель,
– делитель,  –старший коэффициент
–старший коэффициент  (при этом, разумеется, можно предполагать, что
(при этом, разумеется, можно предполагать, что 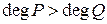 , иначе деление происходит тривиально и модифицированный остаток есть
, иначе деление происходит тривиально и модифицированный остаток есть  – подмножество этого множества, состоящее из многочленов нулевой степени (по переменной x). Тогда диаграмма множества F при данных значениях переменных
– подмножество этого множества, состоящее из многочленов нулевой степени (по переменной x). Тогда диаграмма множества F при данных значениях переменных  .
. . Заметим, что
. Заметим, что  , так как
, так как  , многочлены
, многочлены  и β содержатся в множестве, поэтому знак многочлена
и β содержатся в множестве, поэтому знак многочлена