
|
|
ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИОсновные понятия и формулы Кинематическое уравнение движения материальной точки (центра масс твердого тела)
где r(t) — зависимость радиуса - вектора точки от времени.[1] Мгновенная, средняя и средняя путевая скорости выражаются формулами
где Dr — перемещение, Ds — путь, пройденный точкой за интервал времени Dt. Путь Ds не может убывать и принимать отрицательные значения, т.е. Ds³0. Мгновенное и среднее ускорения
В случае прямолинейного равнопеременного (a=const) движения справедливы формулы
где a>0 для случая равноускоренного движения и a<0 для равнозамедленного. Кинематическое уравнение движения материальной точки по окружности имеет вид:
Угловая скорость
Угловая скорость является псевдовектором (условным вектором). Она параллельна оси вращения точки или тела, а ее направление зависит от направления вращения (направления изменения угла j) и определяется правилом правого винта. Угловое ускорение Направлено также как и угловая скорость в случае ускоренного вращения и в противоположную сторону в случае замедленного. В случае вращения по окружности с постоянным угловым ускорением (ε=const) справедливы формулы
где ε>0 для случая равноускоренного движения по окружности и ε<0 для равнозамедленного. Связь между линейными и угловыми величинами, характеризующими движение точки по окружности:
где v — линейная скорость; aτ и an — тангенциальное и нормальное ускорения; ω — угловая скорость; ε — угловое ускорение; R — радиус окружности. Полное линейное ускорение точки, движущейся по окружности,
Угол между полным а и нормальным an ускорениями
Уравнение гармонических колебаний материальной точки
где х — смещение точки от положения равновесия; А — амплитуда колебаний; ω — круговая или циклическая частота; j — начальная фаза. Скорость и ускорение материальной точки, совершающей гармонические колебания:
Сложение гармонических колебаний одного направления и одинаковой частоты: а) амплитуда результирующего колебания
б) начальная фаза результирующего колебания
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях
а) б) в) Уравнение плоской бегущей волны, распространяющейся в направлении оси x,
где x — смещение из положения равновесия любой из точек среды с координатой х в момент времени t, v — скорость распространения колебаний в среде, j — начальная фаза. Связь разности фаз Dj колебаний точек среды в волне с расстоянием Dх между ними, отсчитанным в направлении распространения колебаний
где l — длина волны. Импульс материальной точки массой m, движущейся со скоростью v
Второй закон Ньютона
где F — результирующая сила, действующая на материальную точку, Fdt - импульс силы, вызвавшей изменение импульса dp. Одна из форм записи второго закона Ньютона для тел с постоянной массой
Силы, рассматриваемые в механике: а) сила упругости
где k — коэффициент упругости (в случае пружины применяется также название — жесткость); х — абсолютная деформация; б) сила тяжести
в) сила гравитационного взаимодействия
где G — гравитационная постоянная; т1 и m2 — массы взаимодействующих тел; r — расстояние между телами (тела рассматриваются как материальные точки); г) сила трения скольжения
где f — коэффициент трения скольжения; N — сила нормального давления. Закон сохранения импульса для системы из N материальных точек
или для двух тел (i=2)
где v1 и v2— скорости тел в начальный момент времени (например, до соударения), u1 и u2— скорости тех же тел в конечный момент времени (например, после соударения). Центр масс (инерции) системы — точка: положение которой определяется радиусом вектором
где ri — радиус-вектор точки системы массой mi. Импульс системы равен произведению массы всей системы на скорость движения ее центра масс
В однородном поле силы тяжести центр масс совпадает с центром тяжести — точкой системы или тела, к которой приложена равнодействующая всех сил тяжести, действующих на систему или тело. Сумма моментов сил тяжести относительно центра тяжести равна нулю. Кинетическая энергия тела, движущегося поступательно,
Потенциальная энергия: а) деформированной упругой пружины
б) гравитационного взаимодействия
в) тела, находящегося в однородном поле силы тяжести
где h — высота тела над уровнем, принятым за нулевой (формула справедлива при условии h<<R, где R—радиус Земли). Закон сохранения механической энергии (выполняется в поле консервативных сил)
Элементарная работаdА, совершаемая результирующей силой F за бесконечно малый промежуток времени dt, определяется как скалярное произведение
где dr — перемещение тела за время dt, a — угол между направлениями силы и перемещения. Работа А, совершаемая результирующей силой, может быть определена также как мера изменения кинетической энергии материальной точки:
Мгновенная мощность определяется формулой
Момент силы материальной точки или тела относительно любой выбранной неподвижной точки (полюса) определяется как векторное произведение
где r — радиус вектор, направленный от полюса к материальной точке или, в случае тела, к точке приложения силы F. Момент импульса материальной точки относительно неподвижной точки (полюса)
где p— импульс точки. В случае тела момент импульса равен векторной сумме моментов импульса всех N точек тела относительно полюса
Основное уравнение динамики вращательного движения тела относительно любой точки (полюса)
где M — результирующий момент внешних сил, действующих на тело, относительно полюса; L — момент импульса тела относительно полюса. Основное уравнение динамики вращательного движения тела относительно неподвижной оси z записывается в форме
или Здесь Мz — результирующий момент внешних сил, действующих на тело, относительно оси z (или проекция на ось z результирующего момента внешних сил M относительно любой точки оси z); ε —угловое ускорение; Jz — момент инерции тела относительно оси вращения z. Значение момента силы Мz определяется как
где F — сила, действующая на тело, l — плечо силы, т.е. кратчайшее расстояние (перпендикуляр) от оси вращения z до прямой, вдоль которой действует сила (линии действия силы). Момент инерции материальной точки массой m относительно оси z
где r — радиус вращения точки вокруг оси z. Момент инерции относительно оси z системы или тела, которые состоят из N материальных точек, равен сумме моментов инерции этих точек относительно данной оси
Моменты инерции некоторых однородных симметричных тел массой m относительно оси симметрии z, проходящей через центр масс: а) стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его середину
б) обруча (или тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (плоскости поперечного сечения цилиндра) и проходящей через его центр
где R — радиус обруча (цилиндра); в) диска (однородного цилиндра) радиусом R относительно оси, перпендикулярной плоскости диска и проходящей через его центр
г) шара радиусом R относительно оси, проходящей через его центр
Момент инерции тела массой m относительно произвольной оси z, не проходящей через центр масс (теорема Штейнера):
где Jc — момент инерции относительно оси, проходящей через центр масс и параллельной оси z, d — расстояние между этими осями. Момент импульса относительно неподвижной оси z тела, вращающегося относительно данной оси с угловой скоростью ω (или проекция момента импульса L тела на ось z),
Закон сохранения момента импульса системы N тел, вращающихся вокруг неподвижной оси z,
Кинетическая энергия тела, вращающегося вокруг неподвижной оси z,
Период физического маятника
где J — момент инерции физического маятника относительно горизонтальной оси, не проходящей через центр масс, d — расстояние от точки подвеса до центра масс. Приведенная длина физического маятника
Период математического маятника
где l — длина математического маятника. Период пружинного маятника
где m — масса маятника, k — жесткость пружины. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
, ,
,  ,
,  ,
, ,
,  .
. ,
,  ,
,  ,
, .
. .
. .
. ,
,  ,
,  ,
, ,
,  ,
,  ,
, или
или  .
. .
. ,
, и
и  .
.
 .
. и
и  :
: , если разность фаз j=0;
, если разность фаз j=0; , если разность фаз j=±p;
, если разность фаз j=±p; , если разность фаз j=±p/2.
, если разность фаз j=±p/2. ,
, ,
, .
. или
или  ,
, .
. ,
, ;
; ,
,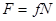 ,
,
 ,
, ,
, .
. или
или 
 ,
, ,
, ,
, .
. ,
, .
. .
. ,
, ,
, ,
, ,
, , если
, если 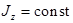 ,
, , если Jz изменяется со временем.
, если Jz изменяется со временем. ,
, ,
, .
. ;
; ,
, ;
; .
.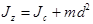 ,
, .
. .
. или
или
 ,
, .
. ,
, ,
,