
|
|
Алгоритмы модулярной арифметикиЕсли взять некое множество взаимно простых натуральных чисел m1, m2, …, mr и число u, меньшее произведения m=m1∙m2∙…∙mr, то u однозначно представимо остатками этого числа (u1, u2, …, ur), где u1=u mod m1, u2=u mod m2, …, ur=u mod mr. И наоборот, совокупности остатков соответствует единственное число по модулю m. Другими словами, между числами u в указанном интервале и совокупностью его остатков по заданным модулям есть взаимно-однозначное соответствие: u ↔ (u1, u2, …, ur). Считаем, что если целое число u рассматривается как (u1, u2, …, ur), то оно имеет модулярное представление. Операциям сложения, вычитания и умножения с числами u и v по модулю m соответствуют покомпонентные операции с их остатками по заданным взаимно простым модулям m1, m2, …, mr. Утверждается, что если u ↔ (u1, u2, …, ur) и v ↔ (v1, v2, …, vr), то (u+v) mod m ↔ ((u1+v1) mod m1, (u2+v2) mod m2, …, (ur+vr) mod mr), (u – v) mod m ↔ ((u1–v1) mod m1, (u2–v2) mod m2, …, (ur–vr) mod mr), (u∙v) mod m ↔ ((u1∙v1) mod m1, (u2∙v2) mod m2, …, (ur∙vr) mod mr). Пример. Пусть m1=3, m2=7 и m3=31. Числа от 0 до 3∙7∙31–1=650 единственным образом представимы через совокупность остатков по данным модулям. Так для чисел 9, 53, 478 имеем: 9=(0, 2, 9), 53=(2, 4, 22), 478=(1, 2, 13). 53+9=62 → (2, 4, 22) + (0, 2, 9) = (2+0, 4+2, 22+9) = (2, 6, 0). 53–9=44 → (2, 4, 22) – (0, 2, 9) = (2–0, 4–2, 22–9) = (2, 2, 13). 53∙9=477 → (2, 4, 22) ∙ (0, 2, 9) = (2∙0, 4∙2, 22∙ 9) = (0, 1, 12). Применим схему вычисления, основанную на китайском алгоритме об остатках, например, к системе сравнений · y1=2 mod 3; · k2=3, t2=3–1 mod 7=5, y2=3∙(5∙(2–2) mod 7)+2=0+2=2; · k3=3∙7=21, t3=21–1 mod 31 =3, y3=21∙(3∙(13–2) mod 31)+2=21∙2+2=44. Для операции умножения имеем: · y1=0 mod 3; · k2=3, t2=3–1 mod 7=5, y2=3∙(5∙(1–0) mod 7)+0=3∙5+0=15; · k3=3∙7=21, t3=21–1 mod 31=2, y3=21∙(2∙(12–1) mod 31) +15 =21∙22+15=477. Итак, операции сложения, вычитания и, самое главное, умножения могут выполняться гораздо быстрее за счет появившейся возможности параллельных (одновременных) действий по различным модулям. К сожалению, этого не скажешь об операциях деления, сравнения, определения знака числа и так далее, а без этого эффективной арифметики не построишь. Логически возможны два пути. Поиск быстродействующих алгоритмов реализации операций в модулярной арифметике или преобразование из модулярного представления в обычное, выполнение операции и обратное преобразование. Но в последнем случае теряется эффект от применения модулярной арифметики, операции перехода затратные. Однако, не все так безнадежно. Рассмотрим вариант реализации модулярной арифметики (его основы), в котором операции преобразования из обычного представления в модулярное и обратно достаточно эффективны. Выберем в качестве модулей mi числа вида Любое целое число u, определенное по модулю числа М. Мерсенна m=2p–1, можно представить p-разрядным словом: В результате сложения чисел u и v, определенным таким образом, получается (p+1)-разрядное число w: w=u+v= Умножение целого числа u на степень 2v по модулю m=2p–1 (w=u∙2v mod (2p–1)) можно представить в виде: w= Поскольку 2p≡1 mod (2p–1) и каждый перенос в разряд p соответствует прибавлению единицы к младшему разряду, то умножение сводится к циклическому сдвигу числа на v разрядов влево. Пример. Пусть p=7, u=83, v=5. Имеем 83∙25 mod 127=116. Двоичное представление числа u=10100112. Циклический сдвиг на 5 разрядов дает число 11101002=11610. Операция умножения многоразрядных чисел реализуется через рассмотренные примитивы (сложение, умножение на число, равное степени двойки). Покажем, что в случае выбора в качестве модулей mi взаимно простых чисел М. Мерсенна для перевода числа u в модулярное представление не требуется выполнять операцию деления. Пример. Пусть m1=22–1=3, m2=23–1=7, m3=25–1=31 и используется 16 разрядов для представления чисел. Тогда m1=0000000000000011, m2=0000000000000111, m3=0000000000011111. Требуется перевести число u=2149210 в модулярное представление. Схема перевода приведена на рис. 1.29. Двоичное представление числа разбивается на группы по i бит (i=2, 3, 5) справа налево. Так как числа 2q∙i (q=0, 1, …,
Рис. 1.29.. Схема перевода числа в модулярное представление Рассмотрим перевод чисел из модулярного представления в обычное, то есть обратимся вновь к анализу китайского алгоритма. В энциклопедии Д. Кнута упоминается коротко о результате Х. Л. Гарнера (1958 год) по способу перехода от модулярного представления числа к его обычному виду, который фактически сводится к ранее рассмотренному четвертому варианту нахождения решения (п. 1.6.2). Напомним, что результат решение системы из r сравнений x≡ci(mod mi) при попарно взаимно простых числах m1, m2,..., mrнаходится путем последовательности вычислений: y1=c1 mod m1, y2=k2∙(t2∙(c2–y1)mod m2)+y1, y3=k3∙(t3∙(c3–y2)mod m3)+y2, ……………………………. yr=kr∙(tr∙(cr–yr–1)mod mr)+yr–1, где Числа ki и ti при известных модулях m1, m2,..., mr можно вычислить заранее, они становятся константами и хранятся в соответствующих элементах одноименных массивов. Тогда логика преобразования сводится к простому повторению операций, выполняемых по модулю чисел М. Мерсенна.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , что соответствует выполненной операции вычитания над остатками. Вычисляем:
, что соответствует выполненной операции вычитания над остатками. Вычисляем: . Вычисляем:
. Вычисляем: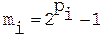 (числа М. Мерсенна, pi – простые числа). Особенность таких чисел в том, что в двоичном представлении они имеют вид 00…01…1. Количество единиц равно pi.
(числа М. Мерсенна, pi – простые числа). Особенность таких чисел в том, что в двоичном представлении они имеют вид 00…01…1. Количество единиц равно pi.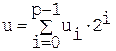 , где ui=(0, 1).
, где ui=(0, 1). +wp∙2p. Поскольку 2p≡1 mod (2p–1), то w=
+wp∙2p. Поскольку 2p≡1 mod (2p–1), то w=  +
+  .
. ) сравнимы с единицей по модулю 2i–1, то остается просуммировать числа (коэффициенты) при соответствующих степенях двойки.
) сравнимы с единицей по модулю 2i–1, то остается просуммировать числа (коэффициенты) при соответствующих степенях двойки.
 и
и  – обратный элемент к ki, такой, что ti∙ki≡1 (mod mi). Значение yr является ответом задачи.
– обратный элемент к ki, такой, что ti∙ki≡1 (mod mi). Значение yr является ответом задачи.