
|
|
В этом случае интегральная ф-ла Лапласа12 Замечание: Иногда в литературе под ф-ей Лапласа подразумевается др. ф-ия
В этом случае интегральная ф-ла Лапласа
В9. Понятие случайной величины и ее закона распределения. Функция распределения случайной величины и ее свойства. График функции распределения случайной величины. Примеры. Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений. Случайная величина обычно обозначается прописной латинской буквой ( Случайные величины делятся на дискретные и непрерывные. 1) Величина называется дискретной, если она может принимать определенные, фиксированные значения. 2) Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга. Законом распределения случайной дискретной величины называется совокупность пар чисел ( Как для дискретной величины, так и для непрерывной вводится понятие функции распределения. Рассмотрим функцию распределения · Если · Если · Если · Аналогично, если Свойства функции распределения: 1) Функция распределения принимает значения из промежутка 2) Вероятность того, что случайная величина примет значение из полуинтервала 3) Функция распределения – неубывающая функция, т.е. 4) 5) Если 6) Если
В10,11. Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Плотность распределения вероятностей случайной величины, являющейся функцией случайной величины. Примеры. Свойства функции распределения: 1) Функция распределения принимает значения из промежутка 2) Вероятность того, что случайная величина примет значение из полуинтервала 3) Функция распределения – неубывающая функция, т.е. 4) 5) Если 6) Если В12. Математическое ожидание дискретной случайной величины и его свойства. Математическое ожидание дискретной случайной величины – это сумма парных произведений всех возможных ее значений на соответствующие вероятности:
где Очевидно, математическое ожидание случайной величины Математическое ожидание Свойства математического ожидания: 1) Теорема. Математическое ожидание постоянной величины 2) Теорема. Математическое ожидание суммы двух (или нескольких) случайных величин
Следствие. Если
3) Теорема. Математическое ожидание произведения двух независимых случайных величин
Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин. Действительно, например, для трех взаимно независимых случайных величин
Следствие. Постоянный множитель можно выносить за знак математического ожидания, т.е. Если
Следствие. Математическое ожидание разности двух случайных величин
В13. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение и моменты дискретной случайной величины. Теорема. Для любой случайной величины
Дисперсией (рассеянием) случайной величины
Очевидно, что дисперсия случайной величины постоянна, т.е. является числовой характеристикой этой величины. Свойства дисперсии можно сформулировать в виде теорем. Теорема. Дисперсия постоянной величины равна нулю. Теорема. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат Теорема. Дисперсия случайной величины равна разности математического ожидания ее квадрата и квадрата математического ожидания самой величины: Теорема. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. Следствие 2. Если Следствие 3. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин, т.е. если случайные величины Средним квадратичным отклонением

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ), ее конкретные значения – строчными буквами (
), ее конкретные значения – строчными буквами (  ).
). ), где
), где  – возможные значения случайной величины, а
– возможные значения случайной величины, а 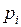 – вероятности, с которыми она принимает эти значения, причем
– вероятности, с которыми она принимает эти значения, причем  .
. случайной дискретной величины
случайной дискретной величины  , принимающей значения
, принимающей значения  .
. , то
, то  , так как в этом случае событие
, так как в этом случае событие  является невозможным.
является невозможным. , то событие
, то событие  , поэтому
, поэтому 
 .
. , то событие
, то событие  и
и 
 .
. , то
, то  .
. :
:  .
. , равна разности
, равна разности  :
:  .
. при
при  .
. .
. , то
, то  .
. , то
, то  .
. ,
, случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины
случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины  равно этой величине.
равно этой величине. равно разности их математических ожиданий:
равно разности их математических ожиданий: .
.
 .
. :
: , и т.д.
, и т.д. .
. .
. .
. .
. .
. .
. .
.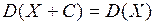 .
. .
. (или стандартом) случайной величины
(или стандартом) случайной величины  этой величины:
этой величины:  .
.