
|
|
Второй этап (получение минимальной формы).Совершенная дизъюнктивная нормальная форма (СДНФ). Дизъюнктивной нормальной формой (ДНФ)называется такая форма представления функции, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждый из которых является простой конъюнкцией аргументов или их инверсий. Если в каждом члене ДНФ представлены все аргументы (или их инверсии) функции, то такая форма носит название совершенной дизъюнктивной нормальной формы (СДНФ).Выражение (3.9) не является СДНФ, так как в нем лишь третий член содержит все аргументы функции. Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, в Совершенная конъюнктивная нормальная форма (СКНФ). Конъюнктивной нормальной формой (КНФ)называется форма представления функции в виде конъюнкции ряда членов, каждый из которых является простой дизъюнкцией аргументов (или их инверсий). Примером КНФ может служить следующая форма представления функции: Приведем формы представления функций, не являющиеся КНФ: (здесь третий член не является простой дизъюнкцией аргументов или их инверсий); (эта форма также не является КНФ, так как в ней первый член не связан с остальными операцией конъюнкции). В совершенной конъюнктивной нормальной форме (СКНФ)в каждом члене КНФ должны быть представлены все аргументы. Для перехода от КНФ к СКНФ необходимо добавить к каждому члену, не содержащему всех аргументов, члены вида , где хi— аргумент, не представленный в члене. Так как ,то такая операция не может повлиять на значение функции. Добавление к некоторому члену образует выражение вида , которое можно привести к виду Справедливость данного равенства вытекает из распределительного закона; она может быть показана также путем раскрытия скобок в правой части выражения: Минимизация логических функций методом квайна Метод Квайнаотносится к числу таких методов минимизации функции алгебры логики, которые позволяют представлять функции в ДНФ или КНФ с минимальным числом членов и минимальным числом букв в членах. Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемойсокращенной форме,на втором этапе—переход от сокращенной формы логического выражения кминимальной форме.
Первый этап (получение сокращенной формы). Пусть заданная функция fпредставлена в СДНФ. Переход к сокращенной форме основан на последовательном применении двух операций: операции склеиванияиоперации поглощения. Для выполнения операции склеивания выявляются в выражении пары членов вида и , различающихся лишь тем, что один из аргументов в одном из членов представлен без инверсии, в другом—с инверсией. Затем проводится склеивание таких пар членов: , и резуль-таты склеивания w вводятся в выражение функции в качестве дополнительных членов. Далее проводится операция поглощения. Она основана на равенстве (член wпоглощает членw? z). При проведении этой операции из логического выражения вычеркиваются все члены, поглощаемые членами, которые введены в результате проведения операции склеивания. Операции склеивания и поглощения проводятся последовательно до тех пор, пока их выполнение оказывается возможным. Второй этап (получение минимальной формы). Сокращенная форма может содержать лишние члены, исключение которых из выражения функции не повлияет на значение функции. Таким образом, дальнейшее упрощение логического выражения достигается исключением из выражения лишних членов. В этом и заключается содержание второго этапа минимизации. Покажем этот этап минимизации логического выражения на примере построения логического устройства для функции в табл. 3.6. рис 3.27
Совершенная ДНФ.данной функции
Для получения сокращенной формы проводим операции склеивания и поглощения Полученное выражение представляет собой сокращенную форму логического выражения заданной функции, а члены его — простые импликантыфункции. Минимизация логических функций методом карт Вейча Метод Квайна имеет четко сформулированные правила проведения отдельных операций, благодаря чему он может быть использован для минимизации функций с использованием ЭВМ в тех случаях, когда минимизируемая функция достаточно сложна (содержит большое число аргументов и каноническая форма имеет большое число членов). Однако для минимизации функции ручным способом (без использования ЭВМ) этот метод оказывается весьма трудоемким. Трудоемкость метода Квайна связана с необходимостью попарного сравнения всех членов выражения для выявления склеиваемых членов. Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется пои минимизации относительно несложных функций (с числом аргументов до 5) ручным способом. В отличие от метода Квайна этот метод требует элементов изобретательности и не может быть использован для решения задачи минимизации с помощью ЭВМ. Карга Вейча прдставляет собой определенную форму таблицы истинности. Табл. 3.10 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов. Каждая клетка карты соответствует определенному набору значений аргументов. Этот набор аргументов определяется присвоением значения лог. 1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 3.10,в) клегки первой строки соответствуют следующим комбинациям аргументов:
Число клеток карты равно числу всех возможных наборов значений аргументов 2n(n– число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности в форме, которая использовалась ранее (табл. 3.11). Таблица истинности этой функции в форме карты Вейча представлена табл. 3.12. Как видим, карта Вейча определяет значения функции на всех возможных наборах значений аргументов и, таким образом, является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При всяком переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.
Сформулируем правила получения МДНФ функций с помощью карт Вейча. Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2k, гдеk= 0, 1, 2, ... Таким образом, допустимое число клеток в области – 1, 2, 4, 8,... Области могут пересекаться и одни и те же клетки могут входить в разные области. Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на kменьше общего числа аргументов функцииn(т. е. равноn – k). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией). Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции). Синтез логических устройств в базисе ИЛИ_НЕ и И-НЕ Построение логического устройства на элементах ИЛИ-НЕ может быть выполнено при следующей последовательности действий: заданная функция минимизируется с получением МКНФ; производится запись полученного логического выражения через операции ИЛИ-НЕ. Рассмотрим последовательность синтеза на примере построения логического устройства, реализующего функцию, приведенную в табл. 3.28. Для минимизации функции воспользуемся методом Вейча. В табл. 3.29 приведена карта Вейча для рассматриваемой функции.
1 2
3. Шифратор Шифраторы – устройства, осуществляющие преобразование десятичных чисел в двоичный код. Шифратор содержит mвходов, последовательно пронумерованных десятичными числами (0,1,2, ..., m-1) и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n-разрядного двоичного кода, соответствующего номеру возведенного входа (таблица 3.5). Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Двоичные шифраторы преобразуют код «1 из N» в двоичный код, т. е. выполняют микрооперацию, обратную микрооперации дешифраторов. При возбуждении одной из входных цепей шифратора на его выходах формируется слово, отображающее номер возбужденной цепи.
Таблица 3.5 – Таблица функционирования шифратора
Полный двоичный шифратор имеет 2n входов и п выходов. Одно из основных применений шифратора – ввод данных с клавиатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры (тетрады двоично-десятичного кода). В этом случае нужен неполный шифратор «10х4» (рисунок 3.11, а), на примере которого рассмотрим принципы построения шифраторов. Из таблицы 3.5 следует, что
Рисунок 3.11 – Схема ввода данных с клавиатуры (а) и дешифратор «10х4» (б)
Для реализации шифратора на элементах ТТЛ, часто применяемых в периферийных устройствах, следует выразить полученные соотношения через операцию И–НЕ. Тогда
На основании этих выражений строится шифратор, показанный на рисунке 3.11, б. Для указания старшей единицы (поиск разряда слова) используют шифраторы приоритета (рисунок 3.12). На вход этого шифратора поступает восьмиразрядное слово (инвертированное), на его выходе в виде трёхразрядного кода вырабатывается номер разряда содержащего старшую единицу.
Рисунок 3.12 – Упрощенная схема шифратора приоритета
Функции Z2, Z1, и Z0 реализующая с помощью комбинационной схемы КС, структура которой определяется полученными выше зависимостями. Кроме того, схема имеет дополнительный вход Вход Указатели старшей единицы с выходом в коде «один из N» можно получить путем дешифрации выхода шифратора приоритетов. Если позволяют требования к быстродействию, то эту же задачу можно решить проще — путем последовательного опроса разрядов в схеме на рисунке 3.13, где единичный сигнал опроса, подаваемый на схему со стороны старшего разряда, может распространяться от разряда к разряду (вправо) только до первого разряда, содержащего единицу. Если в данном разделе нуль, то сигнал опроса пропускается дальше, а на выходе данного разряда остается нулевой сигнал. Если же в данном разряде единица, то на его выходе конъюнктор оказывается блокированным нулевым значением инвертированной переменной и дальнейшее распространение сигнала опроса прекращается. Одновременно на выходе данного разряда возникает единичный сигнал. 4. Дать определение дешифратора. Рассказать о назначении, применении и синтезе дешифратора. Дешифраторы – устройства, предназначенные для преобразования двоичного n-разрядного кода в комбинацию управляющих сигналов. В условных обозначениях дешифраторов и шифраторов используются буквы DC и CD (от слов decoder и coderсоответственно). Двоичные дешифраторы преобразуют двоичный код в код «1 из N». Иными словами, в зависимости от входного кода на выходе возбуждается одна из цепей. Так как с помощью n-разрядного двоичного кода можно отобразить 2п кодовых комбинаций, число выходов полного дешифратора равно 2п. Если часть входных наборов не используется, то дешифратор называют неполным и у него Nвых<2n. Функционирование дешифратора описывается системой логических выражений вида:
где mi – минтермы п входных переменных. В зависимости от разрядности дешифруемого кода и функциональных возможностей логических интегральных схем дешифратор можно выполнить на основе одноступенчатой (или линейной) и многоступенчатой схем дешифрации. Среди многоступенчатых схем можно выделить прямоугольные (матричные) и пирамидальные схемы построения дешифраторов. Дешифраторы широко используются в устройствах вывода информации и управления. Мультиплексор – коммутатор логических сигналов, обеспечивающий передачу информации, поступающей по нескольким входным линиям связи, на одну выходную линию (рисунок 3.14, a). Выбор входной линии Аi осуществляется в соответствии с поступающим адресным кодом. При наличии m адресных входов можно реализовать M=2m комбинаций адресных сигналов, каждая из которых обеспечивает выбор одной из М вводных линий. Мультиплексор состоит из дешифратора адреса входной линии, схем И и схемы объединения ИЛИ. Функциональная схема мультиплексора приведена на рисунке 3.12, б. Двоичный код, воздействующий на адресные входа, откроет одну из схем И, которая соединит с выходом соответствующую входную линию. При этом информация на выходе определяется состоянием выбранного входного канала и не зависит от состояния других каналов.
Мультиплексор «4>1», выполненный на элементах И-ИЛИ-НЕ, показан на рисунке 3.15, а.
Рисунок 3.15 – Схема мультиплексора «4>1» на элементах И-ИЛИ-НЕ (а), схема управления кодом «1 из N» (б), пример обозначения (в)
В условных графических обозначениях функция мультиплексирования именуется MUX (от слова multiplexor). Пример обозначения для мультиплексора «4>1» показан на рисунке 3.15, в. Управление мультиплексором может производиться не только с помощью двоичного кода, но и кодом «1 из N». В этом случае число управляющих входов увеличивается становится равным числу информационных входов (рисунок 3.15, б). Такой режим мультиплексора используется, в частности, в межразрядных цепях реверсивных счетчиков и регистров. В сериях микросхем встречаются мультиплексоры «4>1», «8>1», «16>1» Мультиплексоры на большее число входов, как правило, приходится строить из мультиплексоров меньшей размерности. Если необходим мультиплексор «N>1», а имеются ИМС с числом входов N1, то потребуются L ИMC, где L= N/N1-, которые совместно обеспечат нужное число входов. Для каждой ИМС разрядность управляющего кода составит n1=log2N1, тогда как разрядность управляющего кода всей схемы в целом равна n= log2N- . Число разрядов, равное разности п-ni, используется для организации поочередной передачи выходов отдельных ИМС и общий выходной канал. При этом имеет значение тип выходного каскада ИМС. Если это каскады обычного типа, то потребуется дополнительно объединяющий мультиплексор на выходе схемы (рисунок 3.16).
Рисунок 3.16 – Наращивание размерности мультиплексора
Функционирование такой схемы покажем на конкретных примерах. Пусть, например, управляющий код равен 10101. Значит, на выходах мультиплексоров первого яруса будут сигналы с их пятых информационных входов (y2y1y0=101). На выходной мультиплексор подается управляющий код 10, и на выход схемы попадает сигнал x2 выходного мультиплексора, т. е. пятый выход третьего мультиплексора, номер которого равен 21, что и соответствует двоичному числу 10101. Если ИМС имеют выходы с тремя состояниями, то можно непосредственно объединять эти выходы, а поочередное подключение ИМС к выходной цепи осуществить с помощью дешифратора, управляющего стробирующими входами ИМС (рисунок 3.17). Недостаток такого способа наращивания схем – суммирование емкостей в выходном узле, что в ряде случаев (например, для схем на МОП-транзисторах) может существенно снизить быстродействие мультиплексора.
Рисунок 3.17 – Наращивание размерности мультиплексора, имеющего выходные каскады с тремя состояниями
Мультиплексоры можно использовать для синтеза логических функций от нескольких переменных (x1, x2, …, xn). Если число адресных входов мультиплексора mадр, то из общего числа n переменных функции mадр можно подать на адресные входы. Тогда на информационные входы мультиплексора через дополнительную логическую схему подаются n-mадр переменных. Структуру такой логической схемы можно определить табличным метолом или с помощью диаграмм Вейча.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




 и два дополнительных выхода—
и два дополнительных выхода— 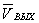 и
и  , обеспечивающие возможность каскадирования шифраторов приоритета для анализа положения старшей единицы в слове, разрядность которого превышает 8.
, обеспечивающие возможность каскадирования шифраторов приоритета для анализа положения старшей единицы в слове, разрядность которого превышает 8.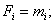
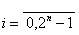
 Рисунок 3.14 – Принцип работы мультиплексора (а), принцип реализации (б)
Рисунок 3.14 – Принцип работы мультиплексора (а), принцип реализации (б)

