
|
|
Лекция11: Алгоритмы обработки данных.Цель лекции: изучить понятие и классификации алгоритмов обработки данных, трудоемкости алгоритмов и методов ее оценки, научиться выработке критериев и оценке трудоемкости алгоритмов с учетом критериев на примере реализаций и задач на языке C++. Понятие "алгоритм обработки данных" в компьютерных науках используется для описания метода решения задачи, который в дальнейшем возможно реализовать в выбранной среде программирования. Тщательная разработка алгоритма является весьма эффективной частью процесса решения задачи в любой области применения. При разработке алгоритма для реальной задачи значительные усилия должны быть потрачены на осознание степени ее сложности, выяснение ограничений на входные данные, разбиение задачи на менее трудоемкие подзадачи. Алгоритм не должен быть привязан к конкретной реализации. В силу разнообразия используемых средств программирования, их требований к аппаратным ресурсам и платформенной зависимости сходные по структуре, но различные в реализации, алгоритмы могут выдавать отличающиеся по эффективности результаты. При этом некоторые среды программирования содержат встроенные библиотечные функции, реализующие базовые алгоритмы обработки данных (например, в MS Visual Studio 2010 в библиотеки С++ входит функция быстрой сортировки массивов данных). Чтобы решения были переносимыми и оставались актуальными, не рекомендуется их ориентировать на процедурную реализацию среды. Поэтому главным в рассматриваемом подходе является выбор метода решения с учетом специфики задачи. Адаптация к среде осуществляется позднее. Выбор того или иного метода обработки данных определяется не только сложностью задачи. Учитывать необходимо и массовость применения разработанного кода: при однократном или редком обращении к реализации предпочтительнее бывают простые алгоритмы, которые несложны в разработке. При этом, однако, допускается возможным увеличение времени работы программы. Массовое использование алгоритмов обработки данных требует поиска наилучшего алгоритма решения. Такой процесс бывает весьма сложен, так как требует выработки критериев оценки и применения математических методов для получения количественных характеристик. Направление компьютерных наук, занимающееся изучением оценки эффективности алгоритмов, называется анализом алгоритмов. Ресурсная эффективность алгоритмов Определение ресурсной эффективности алгоритмов – необходимая составляющая этапа анализа разработанного программного обеспечения. Повышение ресурсной эффективности вычислительных алгоритмов актуально при обработке больших объемов данных, когда аппаратных и/или программных ресурсов может быть недостаточно для корректного завершения работы программного кода. Наиболее значимыми характеристиками ресурсной эффективности алгоритмов являются оценки временной и емкостной сложности, отражающие ресурсы процессора, оперативной памяти, а также внешних носителей данных (при использовании). Под трудоемкостью алгоритма А на входе D будем понимать количество элементарных операций, которые учитываются при анализе алгоритма. Под худшим случаем трудоемкости понимают наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n. Определим лучший случай трудоемкости, как наименьшее количество операций в аналогичном алгоритме и при той же размерности входа. Средний случай трудоемкости определяется средним количеством операций рассматриваемого алгоритма и входных данных. Зависимость трудоемкости алгоритма А от значения параметров на входе D определяетфункцию трудоемкости алгоритма А для входа D. Классический анализ алгоритмов в данном контексте связан, прежде всего, с оценкой временной сложности. Большинство алгоритмов имеют основной параметр, который в значительной степени влияет на время выполнения операций. Если же определяющих параметров несколько, то, как правило, один их них выражается как функция от остальных. Иногда используют и такой подход: рассматривают только один параметр, считая остальные константами. Результатом анализа является асимптотическая оценка выполняемых алгоритмом операций в зависимости от длины входа, которая указывает порядок роста функции и результаты сравнения работы алгоритмов для больших данных. При этом оценка на реальных данных отличается от асимптотической тем, что она ориентирована на конкретные длины входов и число выполняемых алгоритмом операций. Временная сложность алгоритма определяется асимптотической оценкой функции трудоемкости алгоритма для худшего случая, обозначается O(f(n)) и читается как "О большое" или "О-нотация". Асимптотический класс функций О включает в себя как средний, так и лучший случай, потому что запись O(f(n)) обозначает класс функций, скорость роста которых не более, чем f(n) с точностью до некоторой положительной константы. В зависимости от вида функции f(n) выделяют следующие классы сложности алгоритмов.
Классы сложности алгоритмов в зависимости от функции трудоемкости
На основании математических методов исследования асимптотических функций трудоемкости на бесконечности выделены пять классов алгоритмов. Класс Класс Класс Класс Класс Состояние памяти при выполнении алгоритма определяется значениями, требующими для размещения определенных участков. При этом в ходе решения задачи может быть задействовано дополнительное количество ячеек. Под объемом памяти, требуемым алгоритмом А для входа D, понимаем максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма. Емкостная сложность алгоритма определяется как асимптотическая оценка функции объема памяти алгоритма для худшего случая. Таким образом, ресурсная сложность алгоритма в худшем, среднем и лучшем случаях определяется как упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю. Методы оценки ресурсной эффективности алгоритмов Основными алгоритмическими конструкциями в процедурном программировании являются следование, ветвление и цикл. Для получения функций трудоемкости для лучшего, среднего и худшего случаев при фиксированной размерности входа необходимо учесть различия в оценке основных алгоритмических конструкций.
Реализация цикла с предусловием и с постусловием не меняет методики оценки его трудоемкости. На каждом проходе выполняется оценка трудоемкости условия, изменения параметров (при наличии) и тела цикла. Общие рекомендации для оценки циклов с условиями затруднительны. Так как в значительной степени зависят от исходных данных. В случае использования вложенных циклов их трудоемкости перемножаются. Таким образом, для оценки трудоемкости алгоритма может быть сформулирован общий метод получения функции трудоемкости. Декомпозиция алгоритма предполагает выделение в алгоритме базовых конструкций и оценку и трудоемкости. При этом рассматривается следование основных алгоритмических конструкций. Построчный анализ трудоемкости по базовым операциям языка подразумевает либо совокупный анализ (учет всех операций), либо пооперационный анализ (учет трудоемкости каждой операции). Обратная композиция функции трудоемкости на основе методики анализа базовых алгоритмических конструкций для лучшего, среднего и худшего случаев. Особенностью оценки ресурсной эффективности рекурсивных алгоритмов является необходимость учета дополнительных затрат памяти и механизма организации рекурсии. Поэтому трудоемкость рекурсивных реализаций алгоритмов связана с количеством операций, выполняемых при оном рекурсивном вызове, а также с количеством таких вызовов. Учитываются также затраты на возвращения значений и передачу управления в точку вызова. Для анализа трудоемкости механизма рекурсивного вызова-возврата будем учитывать следующие параметры: p – количество передаваемых фактических параметров, r – количество сохраняемых в стеке регистров, k – количество возвращаемых по адресной ссылке значений, l – количество локальных ячеек функции. Тогда функция трудоемкости на одни вызов-возврат примет вид: f=2(p+k+r+l+1), где дополнительная единица учитывает операции с адресом возврата. Оценка требуемой памяти стека может быть получена следующим образом: так как рекурсивные вызовы обрабатываются последовательно, то в конкретный момент времени в стеке хранится не фрагмент дерева рекурсии, а цепочка рекурсивных вызовов – унарный фрагмент дерева. Поэтому объем стека определяется максимально возможным числом одновременно полученных рекурсивных вызовов. Анализ совокупной трудоемкости рекурсивного алгоритма можно выполнять разными способами в зависимости от формирования итоговой суммы базовых операций: по цепочкам рекурсивных вызовов и возвратов, по вершинам рекурсивного дерева. Пример 1. Оценка временной сложности функции пузырьковой сортировки.
//Описание функции сортировки методом "пузырька" void BubbleSort (int k,int x[max]) { int i,j,buf; for (i=k-1;i>0;i--) for (j=0;j<i;j++) if (x[j]>x[j+1]) { buf=x[j]; x[j]=x[j+1]; x[j+1]=buf; } } Оценим временную сложность функции пузырьковой сортировки в худшем случае, т.е. когда исходные данные отсортированы в обратном порядке. В этом случае внутренний цикл для каждого i выполнится i-1 раз и произойдет Оценим временную сложность алгоритма пузырьковой сортировки в среднем случае, т.е. когда исходные данные имеют произвольный порядок. В этом случае условие во внутреннем цикле может выполниться 1,2,...,i-1раз. Складывая, получим Пример 2. Оценка временной сложности функции вычисления биномиального коэффициента
//Описание функции вычисления биномиального коэффициента int Binom (int n,int m) { if (m==0) return 1; //база рекурсии return Binom(n-1,m-1)*n/m; //декомпозиция } Оценим временную сложность функции в худшем случае, т.е. когда m=n. Будет выполнено ( n+1 ) обращений к функции, которая выполнит в n случаях три операции, а в одном возвратит значение. Функция при каждом обращении передает два параметра, не использует локальных переменных, а при возвращении ( n+1 ) раз передает управление в точку вызова. Соответственно сложность алгоритма в худшем случае составит O(n) илиO(m). Оценим временную сложность функции в среднем случае, т.е. когда m<n. При этом выполняются рассуждения, аналогичные худшему случаю, только количество рекурсивных вызовов составит ( m+1 ). Соответственно сложность алгоритма в среднем случае составит O(m). Лучший случай достигается при m=0, когда выполняется единственный вызов функции, передача двух параметров и возвращение в точку вызова, то есть оценка лучшего случая O(1). Базовые алгоритмы обработки данных Базовые алгоритмы обработки данных являются результатом исследований и разработок, проводившихся на протяжении десятков лет. Но они, как и прежде, продолжают играть важную роль во все расширяющемся применении вычислительных процессов. К базовым алгоритмам процедурного программирования можно отнести:
Ключевые термины Алгоритм обработки данных – это описание метода решения задачи в компьютерных науках, который в дальнейшем возможно реализовать в выбранной среде программирования. Анализ алгоритмов – это направление компьютерных наук, занимающееся изучением оценки эффективности алгоритмов. Трудоемкость алгоритма – это количество элементарных операций, которые учитываются при анализе алгоритма. Худший случай трудоемкости – это наибольшее количество операций, задаваемых алгоритмом А на всех входах D определенной размерности n. Лучший случай трудоемкости – это наименьшее количество операций в алгоритме А на всех входах D определенной размерности n. Средний случай трудоемкости – это среднее количество операций в алгоритме А на всех входах D определенной размерности n. Функция трудоемкости алгоритма – это зависимость трудоемкости алгоритма А от значения параметров на входе D. Временная сложность алгоритма – это асимптотическая оценка функции трудоемкости алгоритма для худшего случая. Объем памяти – это максимальное количество ячеек памяти, задействованных в ходе выполнения алгоритма А для входа D. Емкостная сложность алгоритма – это асимптотическая оценка функции объема памяти алгоритма для худшего случая. Ресурсная сложность алгоритма в худшем, среднем и лучшем случаях – это упорядоченная пара классов функций временной и емкостной сложности, заданных асимптотическими обозначениями и соответствующих рассматриваемому случаю. Алгоритмы работы со структурами данных – это алгоритмы, которые определяют базовые принципы и методологию, используемые для получения представление о методах обработки данных. Алгоритмы сортировки – это алгоритмы, предназначенные для упорядочения массивов и файлов. Алгоритмы поиска – это алгоритмы, предназначенные для поиска конкретных элементов в больших коллекциях данных. Алгоритмы на графах – это алгоритмы, предназначенные для реализации стратегий обходов и поиска на графах. Алгоритмы обработки строк – это алгоритмы, которые включают ряд методов обработки последователей символов. Геометрические алгоритмы – это алгоритмы решения задач с использованием геометрических объектов. Краткие итоги 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Когда N удваивается, тогда время выполнения более чем удваивается.
. Когда N удваивается, тогда время выполнения более чем удваивается.
 0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1). Промежуточное состояние занимают алгоритмы со сложностью O(log N), которые также относят к данному классу.
0 – это класс быстрых алгоритмов с постоянным временем выполнения, их функция трудоемкости O(1). Промежуточное состояние занимают алгоритмы со сложностью O(log N), которые также относят к данному классу. обменов. Соответственно сложность алгоритма в худшем случае составит O(k2) обменов.
обменов. Соответственно сложность алгоритма в худшем случае составит O(k2) обменов.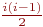 и, соответственно, условие во внутреннем цикле для каждого i выполнится в среднем
и, соответственно, условие во внутреннем цикле для каждого i выполнится в среднем 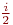 раз и произойдет
раз и произойдет  обменов. Соответственно сложность алгоритма в среднем случае составит O(k2).
обменов. Соответственно сложность алгоритма в среднем случае составит O(k2).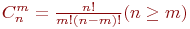 .
.