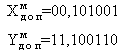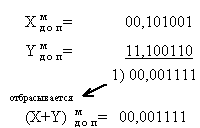|
|
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно.12
При переводе в восьмеричную с.с. двоичное число разбиваем на группы по 3 цифры справа налево начиная с младшего разряда. Затем каждую тройку цифр заменяем соответственно цифрой восьмеричной с.с.. Дробную часть разбиваем от запятой вправо на группы по 3 цифры. Обратный переход - от восьмеричной с.с. к двоичной - осуществляется заменой каждой восьмеричной цифры ее двоичным эквивалентом (тремя двоичными цифрами). Для шестнадцатеричной с.с. - четырьмя двоичными цифрами. Таблица переводов является производной от Таблицы 1,фактически дублируя ее. Таблицы переводов
Примеры 1) Переведите двоичные числа в восьмеричную с.с.. a) б)
2) Переведите двоичные числа в шестнадцатеричную с.с.. a) б)
Перевод смешанных чисел. Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой с.с. целая часть отделяется от дробной запятой (точкой).
Пример Перевести десятичное число 315,1875 в восьмеричную и в шестнадцатеричную с.с.. Из рассмотренных выше примеров следует: 315.187510=473.148=13B.316 .
Основные арифметические операции
Рассмотрим основные арифметические операции: сложение, вычитание,умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным с.с.. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
Таблицы сложения легко составить, используя Правило Счета. Сложение в двоичной системе
Сложение в восьмеричной системе
Сложение в шестнадцатиричной системе
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных с.с..
Шестнадцатеричная: F16+616
Ответ: 15+6 = 2110 = 101012 = 258= 1516.
Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2*81 + 5*80 = 16 + 5 = 21, 1516 = 1*161 + 5*160 = 16+5 = 21.
Пример 2. Сложим числа 15, 7 и 3.
Шестнадцатеричная: F16+716+316
Ответ: 15+7+3 = 2510 = 110012 = 318= 1916.
Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3*81 + 1*80 = 24 + 1 = 25, 1916 = 1*161 + 9*160 = 16+9 = 25
Пример 3. Сложим числа 141,5 и 59,75
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 = 311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду: 11001001,012 = 27 + 26 + 23 + 20 + 2-2 = 201,25 311,28 = 3*82 + 1•81 + 1*80 + 2*8-1 = 201,25 C9,416 = 12*161 + 9*160 + 4*16-1 = 201,25
Вычитание
Пример 1. Вычтем единицу из чисел 102, 108 и 1016
Пример 2. Вычтем единицу из чисел 1002, 1008 и 10016.
Пример 3. Вычтем число 59,75 из числа 201,25.
Ответ: 201,2510 – 59,7510 = 141,510 = 10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду: 10001101,12 = 27 + 23 + 22 + 20 + 2–1 = 141,5; 215,48 = 2*82 + 1*81 + 5*80 + 4*8–1 = 141,5; 8D,816 = 8*161 + D*160 + 8*16–1 = 141,5.
Умножение
Выполняя умножение многозначных чисел в различных позиционных с.с. , можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
Умножение в двоичной системе
Умножение в восьмеричной системе
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
Пример1. Перемножим числа 5 и 6.
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21 = 30; 368 = 3•81 + 6•80 = 30.
Пример 2. Перемножим числа 115 и 51.
Ответ: 115*51 = 586510 = 10110111010012 = 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27 + 26 + 25 + 23 + 20 = 5865; 133518 = 1*84 + 3*83 + 3*82 + 5*81 + 1*80 = 5865.
Деление
Деление в любой позиционной с.с. производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.
Пример 1. Разделим число 30 на число 6.
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 2. Разделим число 5865 на число 115.
Восьмеричная: 133518 :1638
Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20 = 51; 638 = 6*81 + 3*80 = 51.
Пример 3. Разделим число 35 на число 14.
Восьмеричная: 438 : 168
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2*80 + 4*8-1 = 2,5.
3. Формы представления чисел в ЭВМ. При проектировании ЭВМ, создании инструментального и прикладного программного обеспечения разработчикам приходится решать вопрос о представлении в ЭВМ числовых данных. Для решения большинства прикладных задач обычно достаточно использовать целые и вещественные числа. Запись целочисленных данных в запоминающем устройстве ЭВМ не представляет затруднений: число переводится в двоичную систему и записывается в прямом коде. Диапазон представляемых чисел в этом случае ограничивается количеством выделенных для записи разрядов. Для вещественных данных обычно используются две формы записи: число с фиксированной точкой (ЧФТ) и число с плавающей точкой (ЧПТ). 3.1. Числа с фиксированной точкой. Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной техники. Запись числа с фиксированной точкой обычно имеет знаковый и цифровой разряды. Фиксированная точка означает, что на этапе конструирования ЭВМ было определено, сколько и какие разряды машинного слова отведены под изображение целой и дробной частей числа. Запятая в разрядной сетке может быть зафиксирована, в принципе, после любого разряда.
Пример
Как частный случай числа с фиксированной точкой может быть рассмотрена запись целого числа (в этом случае все разряды, кроме знакового, используются для записи целой части).
Пример
К достоинствам использования чисел с фиксированной точкой относятся простота выполнения арифметических операций и высокая точность изображения чисел. К недостаткам - небольшой диапазон представления чисел. 3.2 Числа с плавающей точкой. Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа: N = ± mq ± p где q- основание системы счисления, p - порядок числа, m - мантисса числа N. Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или вправо. 12510=12.5*101=1.25*102=0.125*103=0.0125*104=... Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 1/q ≤ | m | < 1. Таким образом в нормализованных числах цифра после точки должна быть значащей.
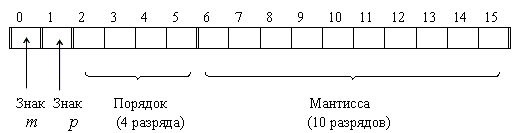
Пример Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка:
б) представление чисел в формате слова
Число А=-3.510=-11.12=-0.111·1010
Максимальным числом представимым в формате слова будет A=(0.1111...1·101111111)2
Таким образом числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от -1·2127 до 1·2127 (2127
4. Основы машинной арифметики с двоичными числами. Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32-разрядный формат (машинное слово), 16-разрядный формат (полуслово) и 64-разрядный формат (двойное слово). 4.1 Коды чисел. В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования: Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт.
Пример В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа -1101 прямой код 1,0001101. Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Пример Для числа +1101 прямой код 0,0001101; обратный код 0,0001101. Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Пример Для числа +1101:
Для числа -1101:
4.2 Особенности сложения чисел в обратном и дополнительном кодах. При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается. При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов. Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также, как и обратный, с последующим прибавлением единицы к младшему разряду.
Пример Сложить двоичные числа X и Y в обратном и дополнительном кодах. а) X= 111, Y= -11; 1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)обр=(X+Y)доп=(X+Y)пр. б) X= -101,Y= -11; 1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код: (X+Y)обр=1,1110100 (X+Y)доп=1,1110101 4.3 Модифицированные обратный и дополнительный коды. При переполнении разрядной сетки, происходит перенос единицы в знаковый разряд. Это приводит к неправильному результату, причем положительное число, получившееся в результате арифметической операции может восприниматься как отрицательное (так как в знаковом разряде "1") и наоборот.
Пример : Здесь X и Y - коды положительных чисел, но ЭВМ воспринимает результат их сложения как код отрицательного числа ("1" в знаковом разряде). Для обнаружения переполнения разрядной сетки вводятся модифицированные коды. В модифицированном обратном и модифицированном дополнительном кодах под знак числа отводится не один, а два разряда: "00" соответствует знаку "+", "11" - знаку "-". Любая другая комбинация ("01" или "10"), получившаяся в знаковых разрядах служит признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах. Рассмотрим предыдущий пример, выполнив сложение в модифицированном обратном коде:
Комбинация "01" в знаковых разрядах означает, что произошло переполнение и получившийся результат - неверный.
Даны два числа: X=101001 и Y= -11010. Сложить их в модифицированном дополнительном коде. 1) Переведем X и Y в модифицированный дополнительный код:
2) Выполним сложение:
Переполнения нет (в знаковых разрядах "00"), поэтому полученный результат - верный (X+Y=1111) 1. Перевести данное число из десятичной системы счисления в двоичную: а) 464(10); б) 380,1875(10); в) 115,94(10) (получить пять знаков после запятой в двоичном представлении).
а) 464 | 0 б) 380 | 0 |1875 в) 115 | 1 |94 232 | 0 190 | 0 0|375 57 | 1 1|88 116 | 0 95 | 1 0|75 28 | 0 1|76 58 | 0 47 | 1 1|5 14 | 0 1|52 29 | 1 23 | 1 1|0 7 | 1 1|04 14 | 0 11 | 1 3 | 1 0|08 7 | 1 5 | 1 1 | 1 0|16 3 | 1 2 | 0 1 | 1 1 | 1
а) 464(10) = 111010000(2); б) 380,1875(10) = 101111100,0011(2); в) 115,94(10) » 1110011,11110(2) (в настоящем случае было получено шесть знаков после запятой, после чего результат был округлен)
Переведем из двоичной системы в восьмеричную число 1111010101,11(2).
001 111 010 101,110(2) = 1725,6(8).
Переведем из двоичной системы в шестнадцатеричную число 1111010101,11(2).
0011 1101 0101,1100(2) = 3D5,C(16).
2. Перевести данное число в десятичную систему счисления. 1000001(2)
1000001(2)=1× 26+0× 25+0× 24+0× 23+0× 22+ 0× 21+1× 20 = 64+1=65(10).
Замечание. Очевидно, что если в каком-либо разряде стоит нуль, то соответствующее слагаемое можно опускать.
б) 1000011111,0101(2).
1000011111,0101(2)=1×29 + 1×24 + 1×23 + 1×22 + 1×21 + 1×20 + 1×2-2 + 1×2-4 = 512 + 16 + 8 + 4 + 2 + 1 + 0,25 + 0,0625 = 543,3125(10).
в) 1216,04(8). 1216,04(8)=1×83+2×82+1×81+6×80+4× 8-2 = 512+128+8+6+0,0625 = 654,0625(10).
г) 29A,5(16).
29A,5(16) = 2×162+9×161+10×160+5×16-1 = 512+144+10+0,3125 = 656,3125(10).
а) 10000000100(2) + 111000010(2) б) 223,2(8) + 427,54(8) в) 3B3,6(16) + 38B,4(16)
10000000100 223,2 3B3,6 + 111000010 + 427,54 +38B,4 ------------ ------- ----- 10111000110 652,74 73E,A
а) 10000000100(2) + 111000010(2) = 10111000110(2). б) 223,2(8) + 427,54(8) = 652,74(8). в) 3B3,6(16) + 38B,4(16) = 73E,A(16).
Выполним проверку результатов расчетов переводом в десятичную систему счисления. Для этого переведем каждое слагаемое и сумму в десятичную систему счисления, выполним сложение слагаемых в десятичной системе счисления. Результат должен совпасть с суммой.
а) 10000000100(2)=1×210+1× 22 = 1024+4=1028(10)
111000010(2)=1×28+ 1×27+ 1×26+ 1×21 = 256+128+64+2 = 450(10)
10111000110(2)=1×210+ 1×28+ 1×27+ 1×26+ 1×22+ 1×21 = 1024+256+128+64+4+2 = 1478(10)
1028(10)+450(10) = 1478(10)
Результаты совпадают, следовательно, вычисления в двоичной системе счисления выполнены верно!
б) 223,2(8)=2×82+ 2×81+ 3×80+ 2×8-1 = 128+16+3+0,25 = 147,25(10)
427,54(8)= 4×82+ 2×81+ 7×80+ 5×8-1+ 4×8-2 = 256+16+7+0,625+0,0625 = 279,6875(10)
652,74(8)= 6×82+ 5×81+ 2×80+ 7×8-1+ 4×8-2 = 384+40+2+0,875+0,0625 = 426,9375(10)
147,25(10)+279,6875(10) = 426,9375(10)
Результаты совпадают, следовательно, вычисления в восьмеричной системе счисления выполнены верно!
в) 3B3,6(16)= 3×162+ 11×161+ 3×160+ 6×16-1 = 768+176+3+0,375 = 947,375(10)
38B,4(16)= 3×162+ 8×161+ 11×160+ 4×16-1 = 768+128+11+0,25 = 907,25(10)
73E,A(16)= 7×82+ 3×81+ 14×80+ 10×8-1 = 1792+48+14+0,625 = 1854,625(10)
947,375(10)+907,25(10) = 1854,625(10)
Результаты совпадают, следовательно, вычисления в шестнадцатеричной системе счисления выполнены верно!
4. Выполнить вычитание: а) 1100000011,011(2) - 101010111,1(2) = 110101011,111(2). б) 1510,2(8) - 1230,54(8) = 257,44(8). в) 27D,D8(16) - 191,2(16) = EC,B8(16).
1100000011,011 1510,2 27D,D8 - 101010111,1 -1230,54 -191,2 -------------- ------- ------ 110101011,111 257,44 EC,B8
5. Выполнить умножение: а) 100111(2) * 1000111(2) б) 1170,64(8) * 46,3(8) в) 61,A(16) * 40,D(16)
100111 1170,64 61,A *1000111 * 46,3 *40,D ------------- -------------- ---------- 100111 355234 4F52 + 100111 + 732470 + 1868 100111 474320 ---------- 100111 ------------- 18B7,52 ------------- 57334,134
а) 100111(2) * 1000111(2) = 101011010001(2). б) 1170,64(8) * 46,3(8) = 57334,134(8). в) 61,A(16) * 40,D(16) = 18B7,52(16).
6. Выполнить деление:
а) 100110010011000(2) : 101011(2) б) 46230(8) : 53(8) в) 4C98(16) : 2B(16)
а) 100110010011000(2) : 101011(2)=111001000(2); б) 46230(8) : 53(8)=710(8); в) 4C98(16) : 2B(16)=1C8(16).
Задачи по теме "Позиционные системы счисления. Арифметические операции"
Задания к работе
1. Перевести данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
2. Перевести данное число в десятичную систему счисления.
3. Сложить числа.
4. Выполнить вычитание.
5. Выполнить умножение.
6. Выполнить деление.
Примечание. В заданиях 3–6 проверять правильность вычислений переводом исходных данных и результатов в десятичную систему счисления. В задании 1д получить пять знаков после запятой в двоичном представлении.
Вариант 1
1. а) 666(10); б) 305(10); в) 153,25(10); г) 162,25(10); д) 248,46(10)
2. а) 1100111011(2); б) 10000000111(2); в) 10110101,1(2); г) 100000110,10101(2); д) 671,24(8); е) 41A,6(16).
3. а) 10000011(2)+1000011(2); б) 1010010000(2)+1101111011(2); в) 110010,101(2)+1011010011,01(2); г) 356,5(8)+1757,04(8); д) 293,8(16)+3CC,98(16).
4. а) 100111001(2)-110110(2); б) 1111001110(2)-111011010(2); в) 1101111011,01(2)-101000010,0111(2); г) 2025,2(8)-131,2(8); д) 2D8,4(16)-A3,B(16).
5. а) 1100110(2)* 1011010(2); б) 2001,6(8)* 125,2(8); в) 2C,4(16)* 12,98(16).
6. а) 110011000(2) : 10001(2); б) 2410(8) : 27(8); в) D4A(16) : 1B(16);
Вариант 2
1. а) 164(10); б) 255(10); в) 712,25(10); г) 670,25(10); д) 11,89(10)
2. а) 1001110011(2); б) 1001000(2); в) 1111100111,01(2); г) 1010001100,101101(2); д) 413,41(8); е) 118,8C(16).
3. а) 1100001100(2)+1100011001(2); б) 110010001(2)+1001101(2); в) 111111111,001(2)+1111111110,0101(2); г) 1443,1(8)+242,44(8); д) 2B4,C(16)+EA,4(16).
4. а) 1001101100(2)-1000010111(2); б) 1010001000(2)-1000110001(2); в) 1101100110,01(2)-111000010,1011(2); г) 1567,3(8)-1125,5(8); д) 416,3(16)-255,3(16).
5. а) 100001(2)* 1001010(2); б) 1723,2(8)* 15,2(8); в) 54,3(16)* 9,6(16).
6. а) 10010100100(2) : 1100(2); б) 2760(8) : 23(8); в) 4AC(16) : 17(16);
Вариант 3
1. а) 273(10); б) 661(10); в) 156,25(10); г) 797,5(10); д) 53,74(10)
2. а) 1100000000(2); б) 1101011111(2); в) 1011001101,00011(2); г) 1011110100,011(2); д) 1017,2(8); е) 111,B(16).
3. а) 1110001000(2)+110100100(2); б) 1001001101(2)+1111000(2); в) 111100010,0101(2)+1111111,01(2); г) 573,04(8)+1577,2(8); д) 108,8(16)+21B,9(16).
4. а) 1010111001(2)-1010001011(2); б) 1110101011(2)-100111000(2); в) 1110111000,011(2)-111001101,001(2); г) 1300,3(8)-464,2(8); д) 37C,4(16)-1D0,2(16).
5. а) 1011010(2)* 1000010(2); б) 632,2(8)* 141,34(8); в) 2A,7(16)* 18,8(16).
6. а) 111010110(2) : 1010(2); б) 4120(8) : 23(8); в) 4F8(16) : 18(16);
Вариант 4 1. а) 105(10); б) 358(10); в) 377,5(10); г) 247,25(10); д) 87,27(10)
2. а) 1100001001(2); б) 1100100101(2); в) 1111110110,01(2); г) 11001100,011(2); д) 112,04(8); е) 334,A(16).
3. а) 101000011(2)+110101010(2); б) 111010010(2)+1011011110(2); в) 10011011,011(2)+1111100001,0011(2); г) 1364,44(8)+1040,2(8); д) 158,A(16)+34,C(16).
4. а) 1111111000(2)-100010011(2); б) 1111101110(2)-11100110(2); в) 1001100100,01(2)-10101001,1(2); г) 1405,3(8)-346,5(8); д) 3DD,4(16)-303,A(16).
5. а) 1011100(2)* 1100100(2); б) 347,2(8)* 125,64(8); в) 10,A8(16)* 35,4(16).
6. а) 1000101000(2) : 1100(2); б) 5101(8) : 31(8); в) D7A(16) : 1E(16);
Вариант 5
1. а) 500(10); б) 675(10); в) 810,25(10); г) 1017,25(10); д) 123,72(10)
2. а) 1101010001(2); б) 100011100(2); в) 1101110001,011011(2); г) 110011000,111001(2); д) 1347,17(8); е) 155,6C(16).
3. а) 1000101101(2)+1100000010(2); б) 1111011010(2)+111001100(2); в) 1001000011,1(2)+10001101,101(2); г) 415,24(8)+1345,04(8); д) 113,B(16)+65,8(16).
4. а) 1101111100(2)-100100010(2); б) 1011010110(2)-1011001110(2); в) 1111011110,1101(2)-1001110111,1(2); г) 1333,2(8)-643,2(8); д) 176,7(16)-E5,4(16).
5. а) 1101100(2)* 1010011(2); б) 516,54(8)* 44,64(8); в) 61,8(16)* 48,9(16).
6. а) 11000100000(2) : 10000(2); б) 3074(8) : 25(8); в) 6D5(16) : 21(16);
Вариант 6
1. а) 218(10); б) 808(10); в) 176,25(10); г) 284,25(10); д) 253,04(10)
2. а) 111000100(2); б) 1011001101(2); в) 10110011,01(2); г) 1010111111,011(2); д) 1665,3(8); е) FA,7(16).
3. а) 11100000(2)+1100000000(2); б) 110101101(2)+111111110(2); в) 10011011,011(2)+1110110100,01(2); г) 1041,2(8)+1141,1(8); д) 3C6,8(16)+B7,5(16).
4. а) 10110010(2)-1010001(2); б) 1101000000(2)-10000000(2); в) 1100101111,1101(2)-100111000,1(2); г) 1621,44(8)-1064,5(8); д) 1AC,B(16)-BD,7(16).
5. а) 1000000(2)* 110110(2); б) 714,34(8)* 133,4(8); в) 16,B(16)* 2B,6(16).
6. а) 10001110011(2) : 10001(2); б) 5456(8) : 33(8); в) 6FA(16) : 13(16);
Вариант 7
1. а) 306(10); б) 467(10); в) 218,5(10); г) 667,25(10); д) 318,87(10)
2. а) 1111000111(2); б) 11010101(2); в) 1001111010,010001(2); г) 1000001111,01(2); д) 465,3(8); е) 252,38(16).
3. а) 1000001101(2)+1100101000(2); б) 1010011110(2)+10001000(2); в) 1100111,00101(2)+101010110,011(2); г) 520,4(8)+635,4(8); д) 2DB,6(16)+15E,6(16).
4. а) 1101000101(2)-111111000(2); б) 11110101(2)-110100(2); в) 1011101011,001(2)-1011001000,01001(2); г) 1034,4(8)-457,44(8); д) 239,A(16)-9C,4(16).
5. а) 1101101(2)* 101010(2); б) 310,2(8)* 40,5(8); в) 18,4(16)* 35,4(16).
6. а) 10101001110(2) : 1110(2); б) 5360(8) : 31(8); в) B80(16) : 20(16);
Вариант 8
1. а) 167(10); б) 113(10); в) 607,5(10); г) 828,25(10); д) 314,71(10)
2. а) 110010001(2); б) 100100000(2); в) 1110011100,111(2); г) 1010111010,1110111(2); д) 704,6(8); е) 367,38(16).
3. а) 10101100(2)+111110010(2); б) 1000000010(2)+110100101(2); в) 1110111010,10011(2)+1011010011,001(2); г) 355,2(8)+562,04(8); д) 1E5,18(16)+3BA,78(16).
4. а) 1010110010(2)-1000000000(2); б) 1111100110(2)-10101111(2); в) 1101001010,101(2)-1100111000,011(2); г) 1134,54(8)-231,2(8); д) 2DE,6(16)-12A,4(16).
5. а) 10101(2)* 11010(2); б) 575,2(8)* 102,2(8); в) 55,4(16)* 6,5(16).
6. а) 1110111000(2) : 1110(2); б) 6457(8) : 33(8); в) AF0(16) : 1C(16);
Вариант 9
1. а) 342(10); б) 374(10); в) 164,25(10); г) 520,375(10); д) 97,14(10).
2. а) 1000110110(2); б) 111100001(2); в) 1110010100,1011001(2); г) 1000000110,00101(2); д) 666,16(8); е) 1C7,68(16).
3. а) 1101010000(2)+1011101001(2); б) 100000101(2)+1100001010(2); в) 1100100001,01001(2)+1110111111,011(2); г) 242,2(8)+1153,5(8); д) 84,8(16)+27E,8(16).
4. а) 1111110(2)-1111011(2); б) 1111100000(2)-111110011(2); в) 1111011111,1001(2)-1010111100,01(2); г) 1241,34(8)-1124,3(8); д) 15F,A(16)-159,4(16).
5. а) 1001010(2)* 1101111(2); б) 1616,3(8)* 61,3(8); в) 3A,38(16)* 64,4(16).
6. а) 10100100000(2) : 10000(2); б) 2756(8) : 26(8); в) D63(16) : 17(16);
Вариант 10
1. а) 524(10); б) 222(10); в) 579,5(10); г) 847,625(10); д) 53,35(10).
2. а) 101111111(2); б) 1111100110(2); в) 10011000,1101011(2); г) 1110001101,1001(2); д) 140,22(8); е) 1DE,54(16).
3. а) 1101010000(2)+11100100(2); б) 100110111(2)+101001000(2); в) 1111100100,11(2)+1111101000,01(2); г) 1476,3(8)+1011,1(8); д) 3E0,A(16)+135,8(16).
4. а) 1010010100(2)-11101110(2); б) 10000001110(2)-10011100(2); в) 1110100111,01(2)-110000001,1(2); г) 1542,5(8)-353,24(8); д) 3EB,8(16)-3BA,8(16).
5. а) 111000(2)* 100111(2); б) 157,4(8)* 101,1(8); в) 19,7(16)* 58,78(16).
6. а) 1111100000(2) : 10000(2); б) 1760(8) : 22(8); в) A17(16) : 15(16);
Вариант 11
1. а) 113(10); б) 875(10); в) 535,1875(10); г) 649,25(10); д) 6,52(10).
2. а) 11101000(2); б) 1010001111(2); в) 1101101000,01(2); г) 1000000101,01011(2); д) 1600,14(8); е) 1E9,4(16).
3. а) 1000111110(2)+1011000101(2); б) 1001000(2)+1101101001(2); в) 110110010,011(2)+1000011111,0001(2); г) 620,2(8)+1453,3(8); д) 348,1(16)+234,4(16).
4. а) 1100001010(2)-10000011(2); б) 1101000001(2)-10000010(2); в) 110010110,011(2)-10010101,1101(2); г) 1520,5(8)-400,2(8); д) 368,4(16)-239,6(16).
5. а) 1100110(2)* 110010(2); б) 177,4(8)* 23,4(8); в) 10,6(16)* 26,8(16).
6. а) 1110010000(2) : 10000(2); б) 4343(8) : 31(8); в) A3B(16) : 1B(16);
Вариант 12
1. а) 294(10); б) 723(10); в) 950,25(10); г) 976,625(10); д) 282,73(10).
2. а) 10000011001(2); б) 10101100(2); в) 1101100,01(2); г) 1110001100,1(2); д) 1053,2(8); е) 200,6(16).
3. а) 1000111110(2)+10111111(2); б) 1111001(2)+110100110(2); в) 1001110101,00011(2)+1001001000,01(2); г) 104,4(8)+1310,62(8); д) 2BD,3(16)+EB,C(16).
4. а) 11110111(2)-11110100(2); б) 1001100111(2)-101100111(2); в) 1100110111,001(2)-1010001101,0011(2); г) 631,1(8)-263,2(8); д) 262,8(16)-1D6,88(16).
5. а) 111101(2)* 1111(2); б) 1751,2(8)* 77,24(8); в) 40,4(16)* 54,6(16).
6. а) 100111000(2) : 1101(2); б) 4120(8) : 23(8); в) 8F6(16) : 1F(16);
Вариант 13
1. а) 617(10); б) 597(10); в) 412,25(10); г) 545,25(10); д) 84,82(10).
2. а) 110111101(2); б) 1110011101(2); в) 111001000,01(2); г) 1100111001,1001(2); д) 1471,17(8); е) 3EC,5(16).
3. а) 1110100100(2)+1010100111(2); б) 1100001100(2)+1010000001(2); в) 1100111101,10101(2)+1100011100,0011(2); г) 750,16(8)+1345,34(8); д) 158,4(16)+396,8(16).
4. а) 10000000010(2)-100000001(2); б) 1110111111(2)-1010001(2); в) 1011001100,1(2)-100100011,01(2); г) 1110,62(8)-210,46(8); д) 1D8,D8(16)-110,4(16).
5. а) 11001(2)* 1011100(2); б) 1440,4(8)* 17,6(8); в) 14,8(16)* 4A,3(16).
6. а) 1010100100(2) : 1101(2); б) 1375(8) : 21(8); в) 4C4(16) : 14(16);
Вариант 14
1. а) 1047(10); б) 335(10); в) 814,5(10); г) 518,625(10); д) 198,91(10).
2. а) 1101100000(2); б) 100001010(2); в) 1011010101,1(2); г) 1010011111,1101(2); д) 452,63(8); е) 1E7,08(16).
3. а) 1101100101(2)+100010001(2); б) 1100011(2)+110111011(2); в) 1010101001,01(2)+10011110,11(2); г) 1672,2(8)+266,2(8); д) 18B,A(16)+2E9,2(16).
4. а) 1110111011(2)-100110111(2); б) 1110000101(2)-1001110(2); в) 1011110100,0011(2)-101001011,001(2); г) 1560,22(8)-1142,2(8); д) 1A5,8(16)-7D,A(16).
5. а) 111100(2)* 111100(2); б) 274,5(8)* 31,34(8); в) 13,4(16)* 38,48(16).
6. а) 10011101100(2) : 1110(2); б) 1436(8) : 23(8); в) CD6(16) : 1F(16);
Вариант 15
1. а) 887(10); б) 233(10); в) 801,5(10); г) 936,3125(10); д) 218,73(10).
2. а) 1010100001(2); б) 10000010101(2); в) 1011110000,100101(2); г) 1000110001,1011(2); д) 1034,34(8); е) 72,6(16).
3. а) 1010110101(2)+101111001(2); б) 1111100100(2)+100110111(2); в) 111111101,01(2)+1100111100,01(2); г) 106,14(8)+322,5(8); д) 156,98(16)+D3,2(16).
4. а) 1111100100(2)-110101000(2); б) 1110110100(2)-1101010101(2); в) 1100001,0101(2)-1011010,101(2); г) 537,24(8)-510,3(8); д) 392,B(16)-149,5(16).
5. а) 111100(2)* 1101001(2); б) 1567,2(8)* 147,2(8); в) 44,8(16)* 13,6(16).
6. а) 1111001100(2) : 10010(2); б) 5050(8) : 31(8); в) 7EC(16) : 1A(16);
Вариант 16
1. а) 969(10); б) 549(10); в) 973,375(10); г) 508,5(10); д) 281,09(10).
2. а) 10100010(2); б) 1110010111(2); в) 110010010,101(2); г) 1111011100,10011(2); д) 605,02(8); е) 3C8,8(16).
3. а) 1111010100(2)+10000000010(2); б) 101001011(2)+10000000010(2); в) 1011101001,1(2)+1110111,01(2); г) 1053,34(8)+1513,2(8); д) 40A,E8(16)+92,7(16).
4. а) 1001100011(2)-111111110(2); б) 1110001000(2)-1011110(2); в) 10000010111,001(2)-1000010,01(2); г) 553,2(8)-105,5(8); д) 298,9(16)-67,4(16).
5. а) 1110000(2)* 1000101(2); б) 436,2(8)* 57,14(8); в) 61,4(16)* 1E,B8(16).
6. а) 10001001100(2) : 1010(2); б) 5203(8) : 27(8); в) D58(16) : 1C(16);
Вариант 17
1. а) 163(10); б) 566(10); в) 694,375(10); г) 352,375(10); д) 288,61(10).
2. а) 1001101001(2); б) 110011101(2); в) 1000001101,01(2); г) 1010001001,11011(2); д) 247,1(8); е) 81,4(16).
3. а) 1010111011(2)+11001000(2); б) 1111101010(2)+1101100100(2); в) 1100011100,1001(2)+10111100,1(2); г) 1711,6(8)+1763,34(8); д) 30A,4(16)+89,48(16).
4. а) 111100101(2)-1101101(2); б) 1001011100(2)-110110101(2); в) 1110011001,1011(2)-1101101100,11(2); г) 1617,4(8)-1442,6(8); д) 36C,2(16)-38,5(16).
5. а) 1100001(2)* 1011100(2); б) 104,54(8)* 66,3(8); в) 4D,A(16)* 69,6(16).
6. а) 10110000010(2) : 1111(2); б) 3316(8) : 32(8); в) A17(16) : 15(16);
Вариант 18
1. а) 917(10); б) 477(10); в) 74,5(10); г) 792,25(10); д) 84,33(10).
2. а) 1110011100(2); б) 1111101111(2); в) 111110100,101(2); г) 110011110,1000011(2); д) 1446,62(8); е) 9C,D(16).
3. а) 11100101(2)+1110111111(2); б) 1101111(2)+1000010(2); в) 1000010100,011(2)+1111110111,011(2); г) 1664,1(8)+501,3(8); д) 1F0,6(16)+34,4(16).
4. а) 1011110110(2)-1001011001(2); б) 1101101110(2)-1000111000(2); в) 1101110010,01(2)-111110110,01(2); г) 1653,1(8)-415,6(8); д) 1B9,4(16)-1B4,6(16).
5. а) 1010000(2)* 1101011(2); б) 1605,14(8)* 22,04(8); в) 24,4(16)* 5E,4(16).
6. а) 10010101111(2) : 1011(2); б) 5366(8) : 27(8); в) 690(16) : 14(16);
Вариант 19
1. а) 477(10); б) 182(10); в) 863,25(10); г) 882,25(10); д) 75,2(10).
2. а) 101011100(2); б) 1000010011(2); в) 11100011,1(2); г) 100101010,00011(2); д) 1762,7(8); е) 1B5,6(16).
3. а) 1011010111(2)+1011110101(2); б) 1110001001(2)+1110101011(2); в) 1100011000,101(2)+10000010100,1(2); г) 1742,4(8)+456,1(8); д) 29E,3(16)+D8,4(16).
4. а) 1000001000(2)-101110000(2); б) 1111011010(2)-101001001(2); в) 1101101,1011(2)-111110,001(2); г) 1026,66(8)-124,2(8); д) 3E0,2(16)-1EA,2(16).
5. а) 1101101(2)* 100000(2); б) 1355,5(8)* 125,64(8); в) 20,4(16)* 2F,4(16).
6. а) 10000001000(2) : 1100(2); б) 3060(8) : 20(8); в) 88B(16) : 1B(16);
Вариант 20
1. а) 804(10); б) 157(10); в) 207,625(10); г) 435,375(10); д) 30,43(10).
2. а) 10010000(2); б) 11001010(2); в) 1110101100,1011(2); г) 110110101,10111(2); д) 1164,36(8); е) 1D5,C8(16).
3. а) 1100010100(2)+1100011010(2); б) 1001001(2)+1100010001(2); в) 1000110,101(2)+1010010001,001(2); г) 433,4(8)+1774,2(8); д) F7,4(16)+178,4(16).
4. а) 10111110(2)-1100010(2); б) 1111110000(2)-100111011(2); в) 1011011100,011(2)-111011111,1(2); г) 314,54(8)-77,14(8); д) 233,68(16)-DB,4(16).
5. а) 1110010(2)* 1010111(2); б) 242,2(8)* 73,2(8); в) 1D,A(16)* 8,4(16).
6. а) 11101100000(2) : 10000(2); б) 3366(8) : 22(8); в) A1E(16) : 25(16);
Вариант 21
1. а) 753(10); б) 404(10); в) 111,1875(10); г) 907,0625(10); д) 62,88(10).
2. а) 11100011(2); б) 1111001111(2); в) 1011111111,01001(2); г) 1001011101,011(2); д) 615,72(8); е) 3DA,5(16).
3. а) 1100101011(2)+1010110010(2); б) 110100111(2)+1100100010(2); в) 1100110100,0011(2)+1101110000,01(2); г) 477,2(8)+647,4(8); д) 372,4(16)+1F0,4(16).
4. а) 1001100000(2)-111001000(2); б) 1100001110(2)-110000001(2); в) 1100110100,01(2)-101100010,101(2); г) 543,46(8)-517,2(8); д) 284,B(16)-77,4(16).
5. а) 1100010(2)* 100001(2); б) 1324,2(8)* 75,54(8); в) 66,D(16)* 1C,D(16).
6. а) 1110110101(2) : 1101(2); б) 5366(8) : 27(8); в) 76C(16) : 19(16);
Вариант 22 1. а) 571(10); б) 556(10); в) 696,25(10); г) 580,375(10); д) 106,67(10).
2. а) 110011010(2); б) 111001010(2); в) 1000010011,00101(2); г) 11010110,00001(2); д) 1343,66(8); е) 3C3,6(16).
3. а) 1100101100(2)+11010000(2); б) 101110110(2)+11111101(2); в) 1001110001,01(2)+1101000111,00101(2); г) 1213,34(8)+1012,34(8); д) 3FE,58(16)+339,7(16).

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


















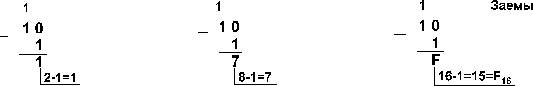









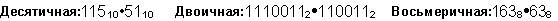



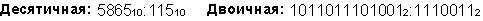










 (1·2127)10.
(1·2127)10.








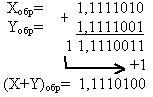

 (X+Y)пр=1,0001011;
(X+Y)пр=1,0001011;