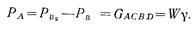|
|
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ СТЕНКУИспользуем основное уравнение гидростатики (2.2) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 12). Вычислим силу давления Р, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
Ось ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось оу—перпендикулярно этой линии в плоскости стенки.
т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади. Если давление ро является атмосферным, то сила избыточного давления жидкости на плоскую стенку равна
Найдем теперь положение центра давления, т. е. координату точки пересечения силы давления жидкости на стенку с плоскостью стенки. Так как внешнее давление ро передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади. Точка приложения силы Ризб (точка D) расположена ниже центра тяжести площади стенки; расстояние между ними равно
Jx0 – момент инерции площади S относительно центральной оси, параллельной ox. Если давление ро равно атмосферному и оно действует с обеих сторон стенки, то точка D и будет центром давления. Когда же роявляется повышенным, то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: hcgS и poS. При этом, чем больше вторая сила по сравнению с первой, тем, очевидно, ближе центр давления к центру тяжести площади S. Выше было дано определение лишь одной координаты центра давления yD. Для определения другой его координаты—xD следует составить уравнение моментов относительно оси Оу. В авиационной технике приходится часто сталкиваться с действием силы давления жидкости на плоские стенки, например, на стенки поршней различных гидростатических машин и устройств, при этом давление ро обычно бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки.
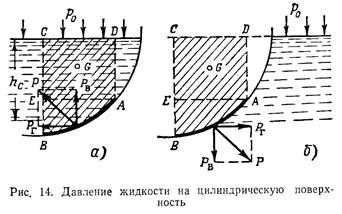
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ЦИЛИНДРИЧЕСКИЕ И СФЕРИЧЕСКИЕ ПОВЕРХНОСТИ. ЗАКОН АРХИМЕДА Решение задачи о силе давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего приходится иметь дело с цилиндрическими или сферическими поверхностями, имеющими вертикальную плоскость симметрии. Давление жидкости в этих случаях сводится к равнодействующей силе, лежащей в плоскости симметрии. Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной плоскости чертежа (рис. 14), и попытаемся определить силу давления жидкости на эту поверхность в двух случаях: жидкость расположена сверху (а) и жидкость расположена снизу (б).
В случае «а» выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия и вертикальном и горизонтальном направлениях. Если жидкость действует на поверхность АВ с силой Р, то поверхность ав оказывает на жидкость такое же давление Р, но направленное в обратную сторону. На рис. 14 показана эта сила реакции, разложенная на две составляющие: горизонтальную Рг и вертикальную Рв. Условие равновесия объема ABCD в вертикальном направлении имеет вид:
где ро—давление на свободной поверхности жидкости; Sг- площадь горизонтальной проекции поверхности АВ; G - вес выделенного объема жидкости.
Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверхности АВ—Sв: Определив по формулам (2.13) и (2.14) вертикальную и горизонтальную составляющие полной силы давления Р, найдем эту силу:
В том случае, когда жидкость расположена снизу (случай «б», см. рис. 14), величина гидростатического давления во всех точках поверхности АВ будет иметь те же значения, что и в случае «а», но направление его будет противоположным и суммарные силы Рв и Ргбудут определяться теми же формулами (2.8) и (2.9), но с обратным знаком. При этом под величиной G следует понимать, так же как и в случае «а», вес жидкости в объеме ABCD, хотя этот объем и не заполнен жидкостью. Положение центра давления на цилиндрической стенке легко может быть найдено, если известны силы Рв и Рг и если определен центр давления на вертикальной проекции стенки или центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой, так как равнодействующая сила при этом пересекает ось поверхности. Это следует из того, что любая элементарная сила давления dP нормальна к поверхности, т. е. направлена по радиусу. Изложенный способ определения силы давления на цилиндрические поверхности применим также и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии. Применим описанный выше прием нахождения вертикальной составляющей силы давления жидкости на криволинейную стенку для доказательства известного закона Архимеда.
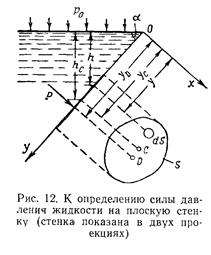
иерхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АСВ от нижней его части ADB. Вертикальная составляющая силы избыточного давления жидкости на верхнюю часть поверхности тела Рв1, направлена вниз и равна весу жидкости в объеме AA'B'BCA. Вертикальная составляющая силы давления жидкости на нижнюю часть поверхности тела Рв2, направлена вверх и равна весу жидкости в объеме AA'B'BDA. Отсюда следует, что вертикальная равнодействующая силы давления жидкости на тело будет направлена вверх и равна весу-жидкости в объеме, равном разности указанных двух объемов, т. е. в объеме тела:
В этом и заключается закон Архимеда, обычно формулируемый так: тело, погруженное в жидкость, теряет в своем весе столько, сколько весит вытесненная им жидкость. Закон Архимеда, разумеется, справедлив и для тел, частично погруженных в жидкость. Сила ра называется архимедовой силой или силой поддержания, а точка ее приложения, т. е. центр тяжести объема W, — центром водоизмещения.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
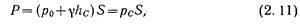
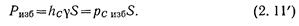
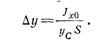



 Пусть в жидкость погружено тело произвольной формы объемом W (рис. 15). Спроектируем это тело на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается по-
Пусть в жидкость погружено тело произвольной формы объемом W (рис. 15). Спроектируем это тело на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается по-