
|
|
Итерационное уточнение решения линейной системы.Лабораторная работа №5. Решение систем линейных уравнений. Часть 1. Содержание.
Введение 3. 5.1 Метод Гаусса 3. 5.2 Погрешность решения систем. Нормы матриц. Обусловленность матриц. 5. 5.3 Итерационное уточнение решения линейной системы 8. Задачи для самостоятельного решения 10. Задания к лабораторной работе 12. Приложение 1 13. Литература 15.
Методы численного решения систем линейных уравнений принято разбивать на две группы, К первой группе относят так называемые точные или прямые методы - это алгоритмы позволяющие получить решение за конечное число арифметических операций. Сюда относится метод Крамера, метод Гаусса и метод прогонки[1]. Другую группу составляют приближенные методы, в частности итерационные методы решения систем линейных алгебраических уравнений. Правило Крамера, при решении задач на ЭВМ не применяется, так как требует большого числа арифметических операций, и, следовательно, дают большую вычислительную погрешность. Метод Гаусса, как правило, используется для решения систем до порядка Мы уже рассматривали системы уравнений, но эти системы имели низкий порядок и системы задавались точно аналитически. Для систем линейных уравнений эта ситуация не имеет места и поэтому крайне важной становится задача оценки погрешности решения системы, по погрешности поставленной задачи и проблема оптимизации алгоритма, с целью уменьшения вычислительной погрешности.
Метод Гаусса.
Этот метод наиболее часто применяется для решения систем т.к. он имеет два важных достоинства: выбор ведущего элемента, позволяющий минимизировать погрешность и корректный учет влияния ошибок округления. В общем случае гауссово исключение состоит из двух этапов: прямого хода и обратного хода. Прямой ход состоит из Мы всегда будем использовать для системы следующие обозначения:
или в матричном виде:
где Алгоритм в целом может быть компактно записан в матричных обозначениях. Для системы (1) положим:
и умножая равенство (1) слева на матрицу
Это преобразование выполнимо, если элемент В этом состоит первый шаг прямого хода метода Гаусса. Второй шаг состоит в умножении равенства (2) на матрицу
Выполняя
Замечание. При выполнении каждого из шагов прямого хода можно уменьшить вычислительную погрешность, для этого в качестве ведущего элемента следует выбирать максимальный по модулю элемент разрешающего столбца, находящийся ниже элемента стоящего на главной диагонали[3]. Говоря другими словами, при каждом шаге на диагональ переставляется уравнение с максимальным по модулю коэффициентом при исключаемой неизвестной. Далее выполняя обратный ход, получим решение системы. Т.е. для реализации этого алгоритма на ЭВМ достаточно иметь процедуры: перемножения матриц, перестановки строк матрицы и построения
5.2 Погрешность решения системы. Нормы матриц. Обусловленность систем.
Поскольку мы договорились оценивать погрешность решения как расстояние между точным и приближенным решениями системы, то нам потребуется определить норму матрицы, и ее определим, согласованно с определением нормы вектора:
Отсюда непосредственно следует, что (1) удовлетворяет аксиомам нормы
Таким образом, множество
Более того, неравенство (2) является “неулучшаемым”, в том смысле, что для каждой матрицы
Квадратная матрица Если выбрать евклидову норму в качестве нормы вектора, то можно интерпретировать норму матрицы следующим образом: При выполнении линейного преобразования Мы интерпретировали только одну из возможных норм векторов. Две другие, обычно используемые в численном анализе нормы таковы:
Эти две нормы порождают соответствующие матричные нормы:
Предлагается, в качестве упражнения, интерпретировать их в двух и трехмерном пространствах. Для расчета погрешности решений системы будем вначале полагать, что матрица системы задана точно, а вектор правых частей приближенно
так как
Предполагая, что
Для любой невырожденной матрицы определим сейчас ее число обусловленности, обозначаемое
Теперь это соотношение можно интерпретировать следующим образом: До сих пор мы предполагали, что матрица A известна точно, вектор правых частей имеет неопределенность. Предположим теперь, что матрица A известна приближенно
тогда
найдем
Объединяя полученные результаты, мы будем иметь соотношение для погрешности решения системы вследствие представления данных в арифметике с плавающей запятой[7]
где Все результаты рассмотрения можно сформулировать в окончательном виде: Предположим, что все элементы
Здесь Второе неравенство утверждает, что, как правило, можно рассчитывать на то, что относительная невязка будет иметь величину, сравнимую с ошибкой округления, независимо от того, насколько плохо обусловлена матрица.
Итерационное уточнение решения линейной системы.
Несмотря на то, что ошибки округления, как правило, невелики, иногда возникает необходимость получить решение с более высокой точностью. Ключом для улучшения точности первого решения
Если мы знаем
Если мы не знаем
Заметим, что каждая система
Как нетрудно видеть перестановку
Исключительно важно, чтобы вычисление невязок Детальный анализ ошибок округления дан в предыдущем параграфе, сходимость процесса итерационного уточнения решения мы рассмотрим чуть позже, а сейчас дадим некоторое правдоподобное представление о природе алгоритма. В частности, мы покажем, что величина Замечание. Ошибка
По результатам предыдущего параграфа имеем
Используя предыдущее равенство и замечание, имеем:
Следовательно, при
Если
т. е. у После вычисления
Задачи для самостоятельного решения. №1. Доказать, имеет место неравенство №2. Доказать, что имеют место равенства: а) б) где нормы матриц согласованы с соответствующими нормами векторов. №3. Пусть
Собственные значения матрицы а) Описать множество б) Найти в) Рассмотрим систему уравнений
1) Какова наименьшая верхняя граница для абсолютной ошибки 2) Какова наименьшая верхняя граница для относительной ошибки
№4. Пусть
Доказать, что данная матрица имеет наибольшее число обусловленности № 5. Пусть № 6. Найти евклидову норму диагональной матрицы. № 7. Найти евклидову норму ортогональной матрицы.
№ 8. Показать, что на основании следующего алгоритма можно получить оценку числа обусловленности матрицы, по норме, согласованной с векторной
где
Задания к лабораторной работе.
Решить системы уравнений, с максимально возможной точностью, для данных одинарной точности :
Основная матрица системы порядка Вектор правых частей, в каждом варианте получается расчетом значений функции Порядок выполнения работы: 1. Составить и отладить процедуры, реализующие прямой ход метода Гаусса. 2. На основании полученных процедур составить подпрограмму расчета 3. Составить и отладить подпрограмму расчета числа обусловленности матрицы 4. Выполнить обратный ход метода Гаусса. 5. Провести расчет невязки и уточнить полученное решение.
Приложение 1.
Вычисление нормы матрицы согласованной с евклидовой нормой вектора.
Мы уже отмечали, что величина нормы матрицы и число обусловленности зависят от выбора типа нормы. Если для норм Для подсчета евклидовой нормы матрицы
следовательно, матрица
эти числа называют сингулярными числами матрицы
где
Тогда
тогда Теорема. Для любой невырожденной матрицы
Из этой теоремы следует, что
Для этого представим
После
Перепишем последнее равенство в виде:
где в первой сумме выписаны собственные векторы, принадлежащие собственному значению
Переходя к пределу, при
Переходя в этом соотношении к норме, получим искомый результат:
Минимальное собственное значение
Замечание. При реализации итерационного процесса основанного на формуле (1), для сокращения числа арифметических операций дробь в правой части формулы можно вычислять не для всех значений
Литература. 1. Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. М:, Наука, 1987. 2. Дж. Форсайт, М. Малькольм, К. Моулер Машинные методы математических вычислений. М., “Мир” 1980. 3. В.В. Воеводин Вычислительные основы линейной алгебры. М., “Наука”, 1977. 4. Е.А. Волков Численные методы. М., “Наука”, 1987. 6. Дж. Форсайт, К. Моулер Численное решение систем линейных алгебраических уравнений. М. “Мир”, 1969. 7. В. В. Смелов. Основы методов вычислительной математики. НГУ 1986. [1] Вариант метода Гаусса, для систем специального вида. [2] Если при выполнении -того шага =0, то перестановкой строк с номером большим можно добиться чтобы 0, если система однозначно разрешима. [3] Поскольку при делении на малое число происходит рост погрешности. [4] -матрица состоящая из нулей. [5] Мы предполагаем, что преобразование невырождено. [6] Таким образом, число обусловленности зависит от используемой нормы. [7] Естественно мы предполагаем, что ошибка возникает только вследствие приближенного представления системы. [8] Это обозначение показывает, что число обусловленности подсчитывается по норме согласованной с евклидовой. [9] Обычно вместо вычисления числа обусловленности получают только его оценку. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а итерационные методы – до порядка
, а итерационные методы – до порядка  .
. шагов. На
шагов. На  -том шаге кратные
-том шаге кратные  , затем предпоследнего уравнения относительно
, затем предпоследнего уравнения относительно  и т.д., пока из первого уравнения не будет вычислено
и т.д., пока из первого уравнения не будет вычислено  .
. (1a)
(1a) , (1b)
, (1b) ,
,  ,
,  .
. 
 ,
, получим систему:
получим систему: (2).
(2). , называемый ведущим, не равен нулю.
, называемый ведущим, не равен нулю. .
. шагов прямого хода[2], получим систему с матрицей верхнего треугольного вида, у которой на главной диагонали стоят единицы
шагов прямого хода[2], получим систему с матрицей верхнего треугольного вида, у которой на главной диагонали стоят единицы .
. матрицы. Для законченности алгоритма необходимо уметь подсчитывать погрешность решения системы, чем мы и займемся в следующем параграфе.
матрицы. Для законченности алгоритма необходимо уметь подсчитывать погрешность решения системы, чем мы и займемся в следующем параграфе. (1).
(1). , для
, для  [4].
[4]. матриц может быть интерпретировано как нормированное векторное пространство размерности
матриц может быть интерпретировано как нормированное векторное пространство размерности 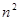 . Также из (1) следует, что
. Также из (1) следует, что . (2)
. (2) найдется вектор
найдется вектор  , такой, что
, такой, что .
. , можно считать, что формула (1) определяет
, можно считать, что формула (1) определяет  как наибольшую длину образа вектора единичной сферы
как наибольшую длину образа вектора единичной сферы  при преобразовании
при преобразовании  , представляет собой длину максимальной полуоси эллипсоида. Или, что норма диагональной матрицы равна максимальному по модулю элементу диагонали. Также следует, что умножение матрицы на любую ортогональную матрицу не изменяет ее нормы.
, представляет собой длину максимальной полуоси эллипсоида. Или, что норма диагональной матрицы равна максимальному по модулю элементу диагонали. Также следует, что умножение матрицы на любую ортогональную матрицу не изменяет ее нормы.
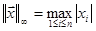 .
.
 .
. и выясним, как велико может быть
и выясним, как велико может быть 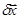 . Имеем следующую цепочку соотношений:
. Имеем следующую цепочку соотношений:


 ,
, , то
, то  . Перемножая, обе части последних неравенств, имеем:
. Перемножая, обе части последних неравенств, имеем: .
. , получим
, получим .
. , как произведение
, как произведение 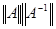 [6] и предыдущая формула перепишется в виде
[6] и предыдущая формула перепишется в виде . (3)
. (3) есть мера относительной неопределенности в задании вектора
есть мера относительной неопределенности в задании вектора  . Аналогично
. Аналогично  можно интерпретировать как меру относительной неопределенности вектора решения системы. Поскольку неравенство является не улучшаемым, то правая часть (3) есть предельная относительная погрешность.
можно интерпретировать как меру относительной неопределенности вектора решения системы. Поскольку неравенство является не улучшаемым, то правая часть (3) есть предельная относительная погрешность. ,
, , после этого, воспользовавшись тождеством
, после этого, воспользовавшись тождеством ,
,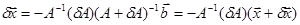 . Переходя в этой формуле к нормам: получаем
. Переходя в этой формуле к нормам: получаем .
. ,
, -вычисленное решение,
-вычисленное решение,  -основание системы счисления,
-основание системы счисления, 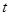 -длина разрядной сетки мантиссы. Следует заметить, что этот вывод справедлив, если мы пренебрегаем погрешностью возникающей при выполнении арифметических операций. Это предположение оправдано тем обстоятельством, что если эта погрешность и возникает, то она минимизируется выбором ведущего элемента при прямом ходе метода Гаусса.
-длина разрядной сетки мантиссы. Следует заметить, что этот вывод справедлив, если мы пренебрегаем погрешностью возникающей при выполнении арифметических операций. Это предположение оправдано тем обстоятельством, что если эта погрешность и возникает, то она минимизируется выбором ведущего элемента при прямом ходе метода Гаусса. .
. является вычисление с двойной точностью его невязки
является вычисление с двойной точностью его невязки 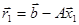 . Зная
. Зная  , мы затем решаем систему
, мы затем решаем систему .
. точно, то
точно, то  будет точным решением системы, потому что
будет точным решением системы, потому что .
. и продолжить процесс уточнения решения: зная
и продолжить процесс уточнения решения: зная  , мы затем решаем систему
, мы затем решаем систему .
. имеет ту же матрицу
имеет ту же матрицу  .
. -той и
-той и 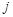 -той строк можно свести к умножению на матрицу
-той строк можно свести к умножению на матрицу  у которой по диагонали, за исключением этих строк, стоят единицы, а в
у которой по диагонали, за исключением этих строк, стоят единицы, а в  .
. выполнялось с более высокой точностью, чем остальные операции. Это основной принцип для любых способов решения уравнения: вычисление невязки является критической операцией, и должно выполнятся точнее других операций.
выполнялось с более высокой точностью, чем остальные операции. Это основной принцип для любых способов решения уравнения: вычисление невязки является критической операцией, и должно выполнятся точнее других операций. к своему предельному вектору. Обратно, последовательность
к своему предельному вектору. Обратно, последовательность  решения системы
решения системы  , таким образом
, таким образом .
. .
. .
.
 .
. , то можно положить
, то можно положить  , в другом случае
, в другом случае ,
, первых разрядов верны, а остальные в пределах погрешности.
первых разрядов верны, а остальные в пределах погрешности.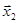 имеет
имеет  верных разрядов.
верных разрядов. .
. имеют следующий вид:
имеют следующий вид: ,
,  .
. , т.е. образ единичной сферы при преобразовании
, т.е. образ единичной сферы при преобразовании  ,
,  ,
,  .
. .
. .
. .
. [8] из всех невырожденных матриц второго порядка, элементами которых являются положительные числа меньшие или равные 100.
[8] из всех невырожденных матриц второго порядка, элементами которых являются положительные числа меньшие или равные 100. есть монотонно убывающая функция
есть монотонно убывающая функция  , при
, при  .
. . Для расчета
. Для расчета  и
и  , для этого решаются две системы уравнений
, для этого решаются две системы уравнений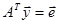 ,
,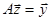 ,
, - вектор с компонентами
- вектор с компонентами  , выбираемый так, чтобы максимизировать
, выбираемый так, чтобы максимизировать  в процессе обратной подстановки для
в процессе обратной подстановки для  .
. .
. одинакова для всех вариантов и ее элементы равны
одинакова для всех вариантов и ее элементы равны  .
. , для
, для  , с шагом
, с шагом  .
. их расчет производится по явным формулам достаточно просто, то вычисление числа обусловленности требует знания обратной матрицы[9], что, вообще говоря, эквивалентно решению системы и поэтому простота расчета указанных норм не гарантирует простоту расчета числа обусловленности матрицы.
их расчет производится по явным формулам достаточно просто, то вычисление числа обусловленности требует знания обратной матрицы[9], что, вообще говоря, эквивалентно решению системы и поэтому простота расчета указанных норм не гарантирует простоту расчета числа обусловленности матрицы. , заметим, что данная матрица является симметричной. Более того, для любого вектора
, заметим, что данная матрица является симметричной. Более того, для любого вектора 
 ,
, положительно определена. Это означает, что все ее
положительно определена. Это означает, что все ее  , причем можно положить
, причем можно положить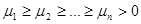 ,
,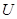 , такую, что
, такую, что ,
, - диагональная матрица с элементами
- диагональная матрица с элементами 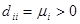 . Теперь определим матрицу
. Теперь определим матрицу 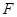 как
как .
. , так что матрица
, так что матрица  является диагональной. Более того, последнее равенство показывает, что различные строки матрицы
является диагональной. Более того, последнее равенство показывает, что различные строки матрицы  . Построим ортонормированную систему вектор-строк
. Построим ортонормированную систему вектор-строк  , для
, для  . Пусть
. Пусть  - матрица строками которой являются вектора
- матрица строками которой являются вектора 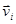
 ,
, и следовательно
и следовательно  . Тем самым доказана:
. Тем самым доказана: , такие, что
, такие, что  диагональная матрица
диагональная матрица 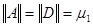 и норма
и норма  , следовательно
, следовательно  . Т.е., для вычисления числа обусловленности матрицы достаточно найти максимальное
. Т.е., для вычисления числа обусловленности матрицы достаточно найти максимальное 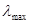 и минимальное
и минимальное  собственные значения матрицы
собственные значения матрицы  и окончательно
и окончательно  . Укажем итерационный алгоритм, принадлежащий Л. А. Люстернику, который позволяет найти наибольшее собственное значение симметричной положительно определенной матрицы
. Укажем итерационный алгоритм, принадлежащий Л. А. Люстернику, который позволяет найти наибольшее собственное значение симметричной положительно определенной матрицы  , причем
, причем  - произвольный ненулевой вектор. Покажем, что
- произвольный ненулевой вектор. Покажем, что .
. матрицы
матрицы  .
. .
.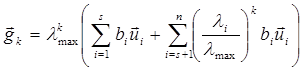 ,
, .
. получим:
получим: .
. максимальное собственное значение матрицы
максимальное собственное значение матрицы  , которое связано с
, которое связано с  .
.