III. Закрепление знаний – решение задач с использованием закона Харди–Вайнберга
Урок 1. Микроэволюция. Закон Харди–Вайнберга
I. Проверка домашнего задания по теме «Популяционная структура вида. Географическая изменчивость в пределах ареала вида»
Работа по карточкам
1. По обе стороны Уральского хребта южнее Екатеринбурга в степях обитают зайцы-русаки. Хотя территории их обитания разделяют горные леса, зайцы внешне неразличимы, а при встречах (южнее Урала) дают плодовитое потомство. Определите, какие формы существования вида составляют эти зайцы?
2. В двух озерах, которые между собой не сообщаются, живут следующие виды рыб: карась, плотва, лещ, язь, судак. Определите, сколько популяций рыб живет в первом озере? Сколько популяций рыб живет во втором озере? Сколько видов рыб живет в двух озерах? Сколько популяций рыб живет в двух озерах?
3. Единицей эволюции считается популяция, а не отдельная особь. Но причиной изменчивости генофонда популяции считают изменение генотипов особей. Объясните, почему.
Устная проверка знаний по вопросам:
1) популяционная структура вида;
2) географическая изменчивость в пределах ареала вида и ее причины; характеристика морфологического критерия вида;
3) клины и подвиды;
4) гибридные зоны и географические изоляты.
II. Изучение нового материала
1. Понятие микро- и макроэволюции.
Эволюция, идущая на уровне ниже вида (подвиды, популяции) и завершающаяся видообразованием, называется микроэволюцией (эволюция популяций под действием естественного отбора).
Микроэволюционные явления и процессы нередко совершаются в относительно небольшие сроки и поэтому доступны для непосредственного наблюдения.
Эволюция на уровне систематических единиц выше вида, протекающая миллионы лет и недоступная непосредственному изучению, называется макроэволюцией.
Процессов макроэволюции мы непосредственно не видим, но можем наблюдать их результаты: современные организмы и ископаемые остатки живших ранее существ.
Термины «микроэволюция» и «макроэволюция» ввел в биологию русский генетик Ю.А. Филиппченко в 1927 г.
Эти два процесса едины, макроэволюция является продолжением микроэволюции. Исследуя движущие силы микроэволюции, можно объяснить1 и макроэволюцию. На уроках мы занимаемся изучением микроэволюционных процессов.
2. Введение в популяционную генетику.
На стыке классического дарвинизма и генетики родилось целое направление – популяционная генетика, занимающаяся изучением эволюционных процессов в популяциях.
Дело в том, что в 20-е гг. XX в. между генетикой и эволюционной теорией Дарвина возникло разногласие. Высказывались мнения о том, что генетика отменила якобы устаревший дарвинизм.
Наши отечественные ученые первыми поняли значение сравнительно мелких объединений особей, на которые распадается население любого вида, – популяций.
В 1926 г. С.С. Четвериков (1880–1959) написал свою главную работу «О некоторых моментах эволюционного процесса с точки зрения современной генетики». Четвериков доказал, что расширение знаний о природе наследственности, наоборот, укрепило и развило дарвинизм.
Выход в свет его работы дал начало синтетической теории эволюции, объединившей генетику и учение Дарвина, – эволюционной генетике.
Популяционная генетика в первую очередь занимается выяснением механизмов микроэволюции.
3. Популяция и генофонд.
Главное начало, объединяющее особей в одну популяцию, – имеющаяся у них возможность свободно скрещиваться между собой – панмиксия (от греч. пан – все и миксис – смешивание). Возможность скрещивания, доступность партнера внутри популяции при этом обязательно должна быть выше, чем возможность встретиться двум особям противоположного пола из разных популяций.
Панмиксия обеспечивает возможность постоянного обмена наследственным материалом. В результате формируется единый генофонд популяции.
Генофонд (от греч. генос – рождение и лат. фонд – основание, запас) – совокупность генов, которые имеются у особей данной популяции (термин введен в биологию в 1928 г. А.С. Серебровским).
4. Частота (концентрация) генов и генотипов.
Важнейшая особенность единого генофонда – его внутренняя неоднородность. Генофонд популяции может быть описан либо частотами генов, либо частотами генотипов.
Предположим, что нас интересует какой-либо ген, локализованный в аутосоме, например ген А, имеющий два аллеля – Аи а. Предположим, что в популяции имеется N особей, различающихся по этой паре аллелей. В популяции встречаются три возможных генотипа – АА; Аа; аа. Введем следующие обозначения:
Д – число гомозигот по доминантному аллелю (АА);
Р – число гомозигот по рецессивному аллелю (аа);
Г – число гетерозигот (Аа).
Общее число аллелей Аможно записать как 2Д + Г, тогда частота встречаемости доминантного аллеля А(обозначается латинской буквой «р») будет равна:
р = (2Д + Г) / N,
где N – число особей.
Частота встречаемости рецессивного аллеля обозначается буквой «g». Ее можно определить, исходя из того, что сумма частот встречаемости аллелей равна единице. Отсюда частота рецессивного аллеля:
g = 1 – р.
Таким образом, мы познакомились с формулами, по которым можно вычислить частоты встречаемости аллелей в генофонде популяции. А каковы частоты встречаемости трех возможных генотипов? На этот вопрос отвечает закон Харди–Вайнберга.
5. Закон Харди–Вайнберга о равновесном состоянии популяций.
Закон о частотах встречаемости генотипов в генофонде популяции был сформулирован независимо друг от друга английским математиком Дж.Харди и немецким генетиком Г.Вайнбергом.
Предположим, что самцы и самки в популяции скрещиваются случайно.
Образование особей с генотипами АА обусловлено вероятностью получения аллеля Аот матери и аллеля Аот отца, т.е.:
р х р = р2 .
Аналогично возникновение генотипа аа, частота встречаемости которого g2.
Генотип Ааможет возникнуть двумя путями: организм получает аллель Аот матери, аллель аот отца или, наоборот, вероятность того и другого события равна р х g, а суммарная вероятность возникновения генотипа Ааравна 2рg.
Таким образом, частоту трех возможных генотипов можно выразить уравнением:
(р + g)2 = р2 + 2рg + g2 = 1,
в котором р – частота встречаемости аллеля А; g – частота встречаемости аллеля а; g2 – частота встречаемости генотипа аа; р2 – частота встречаемости генотипа АА; рg – частота встречаемости генотипаАа.
Таким образом, если скрещивание случайно, то частоты генотипов связаны с частотами аллелей простым уравнением квадрата суммы. Приведенная выше формула получила название уравнения Харди–Вайнберга.
Предположим, что в популяции р = 0,7А, g = 0,3а, тогда частоты встречаемости генотипов будут равны (0,7 + 0,3)2 = 0,49 + 0,42 + 0,09 = 1.
Интересно, что в следующем поколении гаметы с аллелем Абудут вновь возникать с частотой 0,7 (0,49 отАА+ 0,21 от Аа), а с аллелем а– с частотой 0,3 (0,09 от аа+ 0,21 от Аа), т.е. частоты генов и генотипов остаются неизменными из поколения в поколение – это и есть закон Харди–Вайнберга.
6. Условия выполнения закона Харди–Вайнберга.
В полной мере закон Харди–Вайнберга применим к «идеальной популяции», которая характеризуется следующими признаками:
– бесконечно большие размеры;
– неограниченная панмиксия;
– отсутствие мутаций;
– отсутствие иммиграции особей из соседних популяций;
– отсутствие естественного отбора.
В природных популяциях ни одно из этих условий не соблюдается, поэтому и закон Харди–Вайнберга носит условный характер. Тем не менее он реально отражает тенденции в характере распределения частот тех или иных аллелей и генотипов.
III. Закрепление знаний – решение задач с использованием закона Харди–Вайнберга
1.Рассчитать состав идеальной популяции, если генотипом аав ней обладает 1 особь из 400.
Решение
1) g2 = 1/400 (частота гомозиготного генотипа по рецессивному аллелю);
2) частота рецессивного аллеля абудет равна:
g = 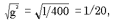 , т.е. 1 часть (один аллель) из 20; , т.е. 1 часть (один аллель) из 20;
3) частота доминантного аллеля будет равна: 20 – 1 = 19;
4) состав популяции: (р + g)2 = р2 + 2рg + g2.
(19 + 1)2 = 192 АА+ 2 х 19 Аа+ 12 аа= 361 АА+ 38 Аа+ 1 аа.
Ответ: 361 АА: 38 Аа: 1 аа.
2. В популяции беспородных собак г. Владивостока было найдено 245 коротконогих животных и 24 с ногами нормальной длины. Коротконогость у собак – доминантный признак (А), нормальная длина ног – рецессивный (а). Определите частоту аллелей Аи аи генотипов АА, Ааи аав данной популяции.
Решение
1) Общее количество собак – 245 + 24 = 269.
Генотип собак с ногами нормальной длины – аа, частоту аллеля а(в долях единицы) обозначаем буквой «g». Тогда частота генотипа аа= g2.
g2 = 24/269 = 0,092
Частота рецессивного аллеля:
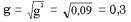
2) Определяем частоту доминантного аллеля А, т.е. р:
р = 1 – g = 1 – 0,3 = 0,7
3) Определяем частоту генотипа АА, т.е. р2:
р2 = 0,72 = 0,49
4) Определяем частоту гетерозигот, то есть 2рg:
2рg = 2 х 0,7 х 0,3 = 0,42
5) Рассчитываем количество собак разных генотипов:
определяем сумму частот доминантных гомозигот и гетерозигот:
0,49 АА+ 0,42 Аа= 0,91;
определяем количество собак с генотипом АА:
245 особей – 0,91
x особей – 0,49,
x = 132 особи;
определяем количество собак с генотипом Аа:
245 особей – 0,91
x особей – 0,42,
x = 113 особей
Ответ: 132 АА: 113 Аа: 24 аа
3. В популяциях Европы из 20 000 человек один – альбинос. Определите генотипическую структуру популяции.
Решение
1) Находим частоту рецессивных гомозигот (g2) в долях единицы:
g2 = 1/20 000 = 0,00005,
тогда частота рецессивного аллеля асоставит:

2) Определяем частоту доминантного аллеля А:
р = 1 – 0,007 = 0,993
3) Определяем частоту генотипа АА, то есть р2:
р2 = 0,9932 = 0,986
4) Определяем частоту генотипа Аа, то есть 2рg:
2рg = 2 х 0,993 х 0,007 = 0,014
5) Расписываем генотипическую структуру популяции европейцев:
0,986 АА: 0,014 Аа: 0,00005 аа, или в расчете на 20 000 человек:
19 720 АА: 280 Аа: 1 аа
Ответ: 0,986 АА: 0,014 Аа: 0,00005 аа, или 19 720 АА: 280 Аа: 1 аа3
IV. Домашнее задание
Изучить параграф учебника (введение в популяционную генетику, закон Харди–Вайнберга) и записи, сделанные в классе.
Решить задачу: «В выборке, состоящей из 84 тыс. растений ржи, 210 растений оказались альбиносами, так как у них рецессивные гены rrнаходятся в гомозиготном состоянии. Определить частоты аллелей Rи rи частоту гетерозиготных растений, несущих признак альбинизма».
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


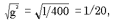 , т.е. 1 часть (один аллель) из 20;
, т.е. 1 часть (один аллель) из 20;